2 Is What Percent Of 16
Treneri
Apr 03, 2025 · 5 min read
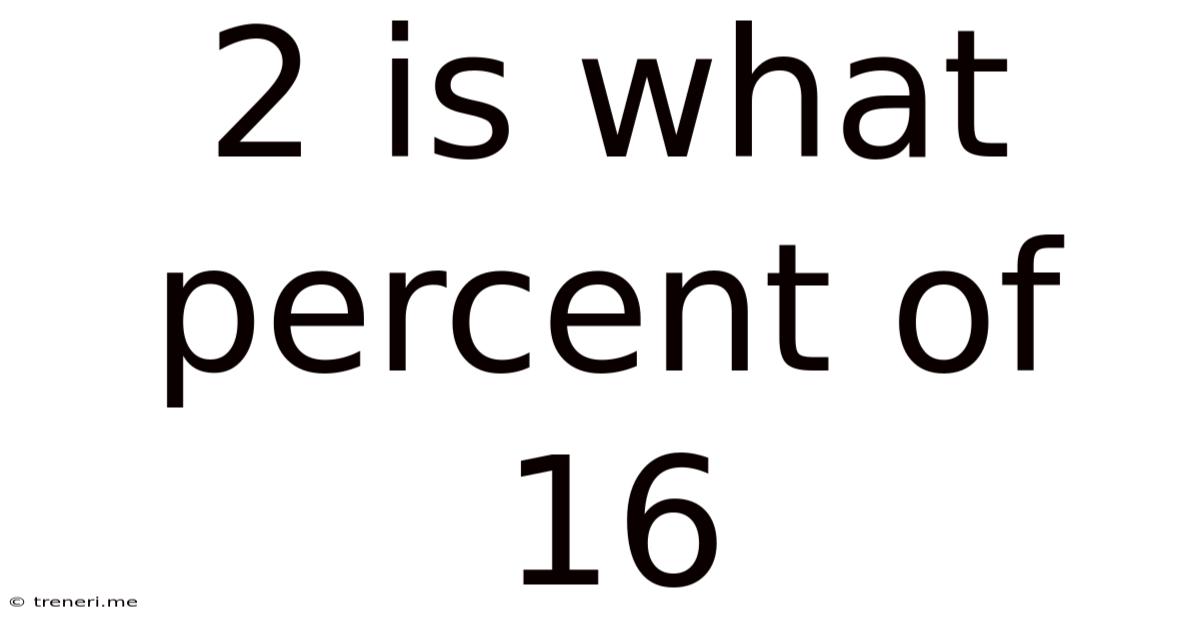
Table of Contents
2 is What Percent of 16? A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill in various aspects of life, from calculating discounts and taxes to analyzing data and understanding statistics. This article will delve into the question, "2 is what percent of 16?", providing a detailed explanation of the process, exploring different calculation methods, and highlighting practical applications. We'll also touch upon the broader context of percentage calculations and their significance.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "out of one hundred." So, 10% means 10 out of 100, which can be written as the fraction 10/100 or the decimal 0.10.
Percentages are incredibly useful because they allow us to compare proportions easily. Whether we're looking at sales figures, test scores, or population demographics, percentages provide a standardized way to understand relative quantities.
Calculating "2 is What Percent of 16?"
To answer the core question, we need to determine what percentage 2 represents of the whole, which is 16. There are several methods to accomplish this:
Method 1: Using the Formula
The most common method involves using the basic percentage formula:
(Part / Whole) x 100% = Percentage
In our case:
- Part: 2
- Whole: 16
Substituting these values into the formula:
(2 / 16) x 100% = 0.125 x 100% = 12.5%
Therefore, 2 is 12.5% of 16.
Method 2: Setting up a Proportion
Another approach involves setting up a proportion:
2/16 = x/100
Here, 'x' represents the percentage we're trying to find. To solve for 'x', we cross-multiply:
16x = 200
x = 200 / 16
x = 12.5
Again, this confirms that 2 is 12.5% of 16.
Method 3: Using Decimal Conversion
We can also convert the fraction 2/16 to a decimal and then multiply by 100%:
2/16 = 0.125
0.125 x 100% = 12.5%
This method demonstrates the direct relationship between fractions, decimals, and percentages.
Practical Applications of Percentage Calculations
The ability to calculate percentages is invaluable in many real-world scenarios:
Finance and Budgeting:
- Calculating discounts: If a store offers a 20% discount on an item priced at $50, you can quickly calculate the discount amount (20% of $50 = $10) and the final price ($50 - $10 = $40).
- Understanding interest rates: Interest rates on loans, savings accounts, and investments are expressed as percentages. Knowing how to calculate interest is crucial for financial planning.
- Analyzing investment returns: Tracking investment performance often involves calculating percentage changes in portfolio value.
- Calculating taxes: Sales tax, income tax, and other taxes are usually expressed as percentages of income or purchase price.
Data Analysis and Statistics:
- Representing proportions: Percentages provide a clear and concise way to represent proportions within datasets, facilitating comparison and interpretation.
- Creating charts and graphs: Many charts and graphs, such as pie charts and bar graphs, use percentages to visualize data effectively.
- Understanding statistical significance: In statistical analysis, percentages are used to express the probability or significance of results.
Everyday Life:
- Calculating tips: Determining the appropriate tip amount in a restaurant often involves calculating a percentage of the bill.
- Understanding sales and promotions: Analyzing sales and promotional offers frequently requires calculating percentages to assess the best deals.
- Comparing prices: Comparing the prices of similar items from different stores or brands can be facilitated by calculating percentage differences.
Expanding on Percentage Calculations: More Complex Scenarios
While the example "2 is what percent of 16?" is relatively straightforward, percentage calculations can become more complex. Let's consider some variations:
Finding the Whole When the Percentage and Part are Known:
Let's say you know that 25% of a number is 5. How do you find the original number (the whole)? You can set up a proportion:
25/100 = 5/x
Cross-multiplying and solving for x gives you x = 20. Therefore, 25% of 20 is 5.
Finding the Part When the Percentage and Whole are Known:
If you know that you need to pay 6% sales tax on a $100 item, how much is the sales tax? You simply calculate 6% of $100:
(6/100) x $100 = $6
Percentage Increase and Decrease:
Calculating percentage increase or decrease is crucial for tracking changes over time. The formula for percentage change is:
((New Value - Old Value) / Old Value) x 100%
For example, if a stock price increases from $50 to $60, the percentage increase is:
(($60 - $50) / $50) x 100% = 20%
Mastering Percentages: Tips and Tricks
- Practice regularly: The more you practice percentage calculations, the more comfortable and proficient you'll become.
- Use a calculator: For more complex calculations, a calculator can save time and ensure accuracy.
- Understand the concepts: Focusing on understanding the underlying principles, rather than just memorizing formulas, will help you apply the concepts to a wider range of problems.
- Break down complex problems: Complex percentage problems can be broken down into smaller, more manageable steps.
- Check your work: Always double-check your calculations to ensure accuracy.
Conclusion
The question "2 is what percent of 16?" serves as a simple yet powerful illustration of the importance of percentage calculations. Understanding percentages is a fundamental skill applicable across diverse fields, from personal finance to data analysis and beyond. Mastering percentage calculations empowers individuals to make informed decisions, analyze information effectively, and navigate the quantitative aspects of everyday life with confidence. By understanding the different calculation methods and practicing regularly, you can develop proficiency in this essential mathematical skill.
Latest Posts
Latest Posts
-
13 Quarts Equals How Many Gallons
May 09, 2025
-
Cuanto Falta Para El 19 De Junio
May 09, 2025
-
Del 87 Al 2024 Cuantos Anos Son
May 09, 2025
-
How Much Does 17 Oz Of Water Weigh
May 09, 2025
-
The Markdown Percent Is Calculated By
May 09, 2025
Related Post
Thank you for visiting our website which covers about 2 Is What Percent Of 16 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.