2 Is What Percent Of 200
Treneri
May 09, 2025 · 5 min read
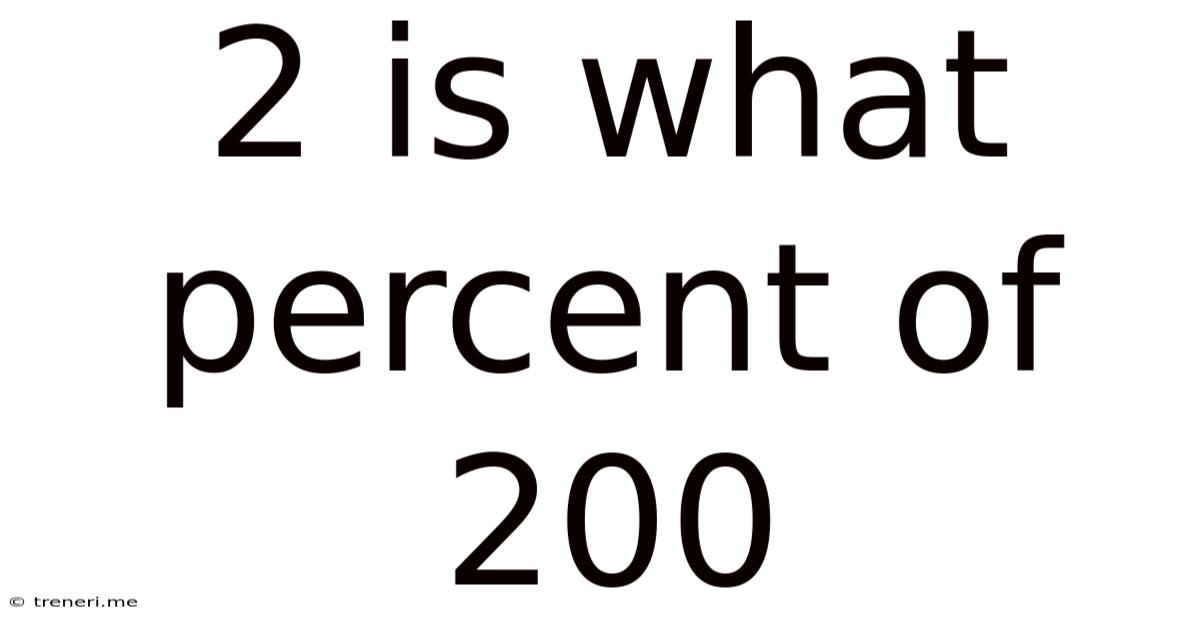
Table of Contents
2 is What Percent of 200? A Deep Dive into Percentage Calculations
Understanding percentages is a fundamental skill in various aspects of life, from calculating discounts and tax rates to comprehending statistical data and financial reports. This article will not only answer the question "2 is what percent of 200?" but also provide a comprehensive guide to percentage calculations, exploring different methods and applications. We'll delve into the underlying concepts, offer practical examples, and discuss how to apply these skills in real-world scenarios. By the end, you'll be confident in tackling any percentage problem that comes your way.
Understanding Percentages: The Basics
A percentage is a fraction or ratio expressed as a number out of 100. The term "percent" literally means "out of one hundred" (per centum in Latin). For instance, 50% means 50 out of 100, which is equivalent to 50/100 or 1/2 (one-half).
Understanding this basic concept is crucial for solving percentage problems. The key elements involved are:
- The Part: This is the smaller quantity we're comparing to the whole. In our example, "2" is the part.
- The Whole: This is the larger quantity to which the part is being compared. In our example, "200" is the whole.
- The Percentage: This is the value expressed as a number out of 100, representing the proportion of the part relative to the whole. This is what we're trying to find.
Calculating Percentages: The Formula
The fundamental formula for calculating percentages is:
(Part / Whole) * 100 = Percentage
Let's apply this formula to our initial question: "2 is what percent of 200?"
-
Identify the Part and the Whole:
- Part = 2
- Whole = 200
-
Apply the Formula:
- (2 / 200) * 100 = 1%
Therefore, 2 is 1% of 200.
Alternative Methods for Calculating Percentages
While the above formula is the most direct approach, there are other methods you can use depending on the complexity of the problem and your personal preference.
Method 1: Using Proportions
This method involves setting up a proportion to solve for the unknown percentage.
-
We know that x% of 200 is equal to 2. We can write this as a proportion: x/100 = 2/200
-
Cross-multiply to solve for x: 200x = 200 x = 1
-
Therefore, x = 1%, confirming our previous result.
Method 2: Using Decimal Equivalents
Percentages can be easily converted to decimals by dividing by 100. For example, 1% is equivalent to 0.01. We can use this to solve our problem:
-
We want to find what percentage 2 is of 200. We can express this as: 2 = x * 200
-
Solving for x: x = 2 / 200 = 0.01
-
Converting the decimal back to a percentage: 0.01 * 100 = 1%
This method highlights the interchangeable nature of percentages and decimals, making it a flexible approach for solving percentage problems.
Practical Applications of Percentage Calculations
The ability to calculate percentages is a valuable skill applicable in many areas of life:
1. Finance and Budgeting:
- Calculating interest: Understanding compound interest involves calculating percentages over time.
- Determining discounts: Sales often advertise discounts as percentages (e.g., 20% off).
- Analyzing financial statements: Financial reports use percentages extensively to represent key ratios and trends. For instance, profit margins are often expressed as a percentage of revenue.
- Tax calculations: Sales tax, income tax, and other taxes are expressed and calculated as percentages.
2. Statistics and Data Analysis:
- Interpreting survey results: Survey data is frequently presented as percentages to show the proportion of respondents who chose particular options.
- Understanding probability: Probability is often expressed as a percentage, indicating the likelihood of an event occurring.
- Analyzing growth rates: Economic growth, population growth, and other trends are often expressed as percentage changes over time.
3. Everyday Life:
- Calculating tips: Restaurant tips are commonly calculated as a percentage of the bill.
- Determining sale prices: Calculating the final price of a sale item after a percentage discount is a common task.
- Understanding nutrition labels: Nutritional information on food packaging often expresses the percentage of daily recommended values for various nutrients.
Advanced Percentage Calculations: Finding the Whole or the Part
While we've focused on finding the percentage, sometimes you need to find the whole or the part given the percentage and either the whole or the part, respectively. Here's how:
Finding the Whole:
If you know the percentage and the part, you can find the whole using the following formula:
Whole = (Part / Percentage) * 100
Example: 10% of a number is 5. What is the number?
Whole = (5 / 10) * 100 = 50
Finding the Part:
If you know the percentage and the whole, you can find the part using the following formula:
Part = (Percentage / 100) * Whole
Example: What is 25% of 80?
Part = (25 / 100) * 80 = 20
Percentage Increase and Decrease
Percentage increase and decrease calculations are common in various contexts, such as tracking price changes or analyzing growth rates.
Percentage Increase:
The formula for percentage increase is:
[(New Value - Original Value) / Original Value] * 100
Example: A product's price increased from $50 to $60. What is the percentage increase?
Percentage Increase = [(60 - 50) / 50] * 100 = 20%
Percentage Decrease:
The formula for percentage decrease is:
[(Original Value - New Value) / Original Value] * 100
Example: A product's price decreased from $100 to $80. What is the percentage decrease?
Percentage Decrease = [(100 - 80) / 100] * 100 = 20%
Mastering Percentages: Practice and Resources
The key to mastering percentage calculations is consistent practice. Try solving various percentage problems using different methods to reinforce your understanding. Numerous online resources, including interactive calculators and practice exercises, can further enhance your skills.
Conclusion
Understanding and calculating percentages is a vital skill with wide-ranging applications. From everyday financial transactions to complex data analysis, the ability to work with percentages effectively is essential. By mastering the fundamental formulas and practicing regularly, you can confidently tackle any percentage problem and leverage this knowledge to make informed decisions in various aspects of your life. Remember, the core principle always revolves around the relationship between the part, the whole, and the percentage, expressed as a ratio out of 100.
Latest Posts
Latest Posts
-
8 30 To 3 Is How Many Hours
May 09, 2025
-
How Many Cups Is 10 75 Ounces
May 09, 2025
-
How Many Sides Has A Octagon
May 09, 2025
-
What Is The Gcf Of 15 And 18
May 09, 2025
-
What Is 120 Days Before Today
May 09, 2025
Related Post
Thank you for visiting our website which covers about 2 Is What Percent Of 200 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.