2 Is What Percent Of 24
Treneri
May 14, 2025 · 5 min read
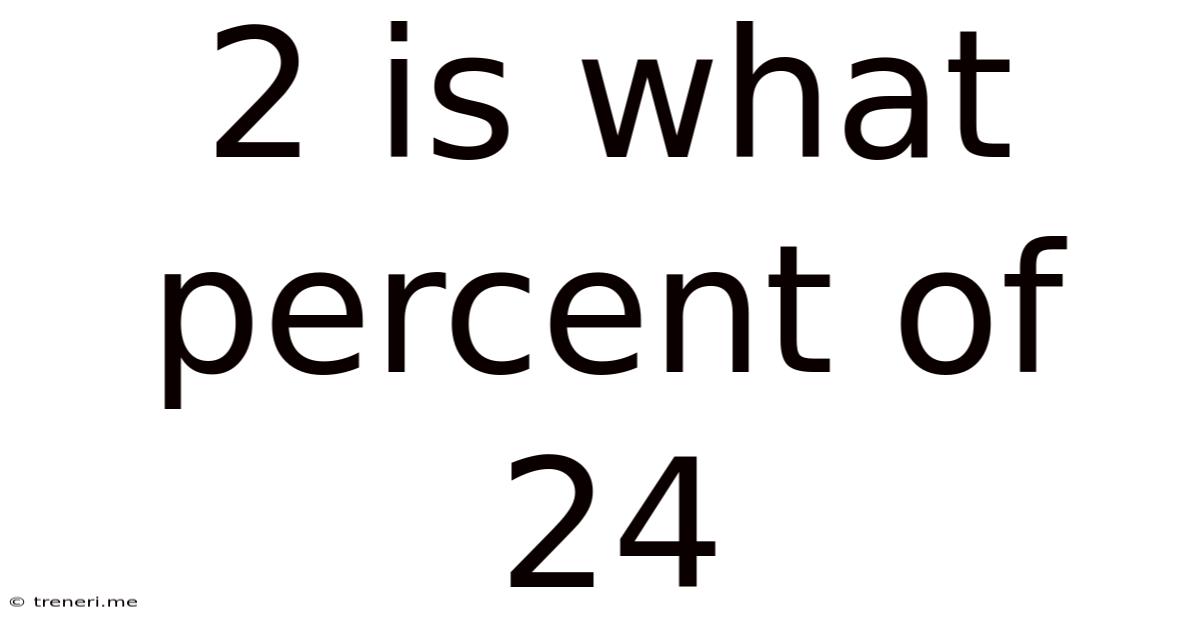
Table of Contents
2 is What Percent of 24? A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill applicable across various fields, from everyday finances to complex scientific calculations. This article delves deep into the question, "2 is what percent of 24?", providing not just the answer but a comprehensive understanding of the underlying principles and methods. We'll explore different approaches to solving percentage problems, demonstrating their versatility and helping you confidently tackle similar calculations in the future.
Understanding Percentages: The Basics
A percentage is a way of expressing a number as a fraction of 100. The term "percent" literally means "per hundred." For example, 50% means 50 out of 100, or 50/100, which simplifies to 1/2. This representation provides a standardized way to compare proportions and fractions.
Key Terms:
- Percent (%): A ratio expressed as a fraction of 100.
- Part: The number that represents a portion of the whole.
- Whole: The total amount or quantity.
Calculating "2 is What Percent of 24?"
There are several ways to solve this problem. Let's explore the most common methods:
Method 1: Using the Formula
The fundamental percentage formula is:
(Part / Whole) x 100 = Percentage
In our case:
- Part: 2
- Whole: 24
Plugging the values into the formula:
(2 / 24) x 100 = Percentage
Simplifying the fraction:
(1 / 12) x 100 = Percentage
Performing the calculation:
0.08333... x 100 ≈ 8.33%
Therefore, 2 is approximately 8.33% of 24.
Method 2: Setting up a Proportion
We can also solve this using proportions. A proportion is a statement that two ratios are equal. We can set up a proportion like this:
2 / 24 = x / 100
Where 'x' represents the percentage we're trying to find.
To solve for 'x', we cross-multiply:
2 x 100 = 24 x x
200 = 24x
x = 200 / 24
x ≈ 8.33
Therefore, 2 is approximately 8.33% of 24.
Method 3: Using Decimal Conversion
We can convert the fraction 2/24 to a decimal and then multiply by 100 to find the percentage.
2 / 24 = 0.08333...
0.08333... x 100 ≈ 8.33%
This method is straightforward and efficient for simple percentage calculations.
Expanding on Percentage Calculations: Real-World Applications
Understanding percentage calculations is crucial for various aspects of life. Let's look at a few real-world examples:
1. Financial Calculations:
- Interest Rates: Banks and financial institutions use percentages to calculate interest on loans and savings accounts.
- Discounts: Stores often offer discounts expressed as percentages (e.g., "20% off").
- Taxes: Sales tax and income tax are calculated as percentages of the purchase price or income.
- Profit Margins: Businesses use percentages to determine their profit margins. For example, a company might aim for a 15% profit margin.
2. Scientific and Statistical Applications:
- Data Analysis: Percentages are used to represent proportions in data sets, such as the percentage of people who prefer a certain product.
- Probability: Probabilities are often expressed as percentages.
- Chemistry: Concentration of solutions is often expressed as a percentage.
3. Everyday Life:
- Tip Calculations: When dining out, people often calculate a tip (usually a percentage of the bill).
- Recipe Scaling: Adjusting ingredient amounts in recipes involves using percentages. For example, doubling a recipe would mean increasing each ingredient by 100%.
- Grading Systems: Many educational systems use percentages to represent grades (e.g., 85%).
Advanced Percentage Problems: Going Beyond the Basics
While the problem "2 is what percent of 24?" is relatively straightforward, let's explore more complex scenarios to enhance your understanding:
Calculating the Whole when the Percentage and Part are Known
Let's say you know that 15% of a number is 6. How do you find the whole number?
We can use the formula:
(Part / Percentage) x 100 = Whole
(6 / 15) x 100 = 40
Therefore, the whole number is 40.
Calculating the Part when the Percentage and Whole are Known
If you know that 25% of a number is 20, how do you calculate the part?
We can adapt the basic percentage formula:
(Percentage / 100) x Whole = Part
(25 / 100) x 20 = 5
Therefore, the part is 5.
Percentage Increase and Decrease
Percentage increase and decrease calculations are frequently encountered in various situations, such as determining price changes or population growth.
Percentage Increase: [(New Value - Old Value) / Old Value] x 100
Percentage Decrease: [(Old Value - New Value) / Old Value] x 100
Practical Tips for Mastering Percentage Calculations
- Practice Regularly: The best way to master percentages is through consistent practice. Try solving different types of percentage problems.
- Use a Calculator: For more complex calculations, using a calculator can save time and ensure accuracy. Many calculators have a percentage function.
- Understand the Concepts: Don't just memorize formulas; understand the underlying principles behind percentage calculations.
- Break Down Complex Problems: If you encounter a complex percentage problem, break it down into smaller, more manageable steps.
- Check Your Work: Always check your work to ensure your answer is reasonable and accurate.
Conclusion: Mastering the Power of Percentages
The seemingly simple question, "2 is what percent of 24?" opens the door to a vast world of percentage calculations. By understanding the fundamental principles, formulas, and various solution methods, you can confidently tackle a wide range of percentage problems encountered in everyday life, academic pursuits, and professional endeavors. Remember that consistent practice and a strong grasp of the underlying concepts are key to mastering this essential mathematical skill. From calculating discounts to understanding financial reports, the ability to work with percentages empowers you to make informed decisions and navigate the numerical world with confidence.
Latest Posts
Latest Posts
-
180 Days From March 26 2024
May 14, 2025
-
Whats The Best Uv To Get Tan
May 14, 2025
-
How Many Calories Do You Burn Running 5k
May 14, 2025
-
Average Price Per Square Foot By Zip Code Calculator
May 14, 2025
-
How Long Is 41 Weeks In Months
May 14, 2025
Related Post
Thank you for visiting our website which covers about 2 Is What Percent Of 24 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.