2 Is What Percent Of 32
Treneri
May 14, 2025 · 5 min read
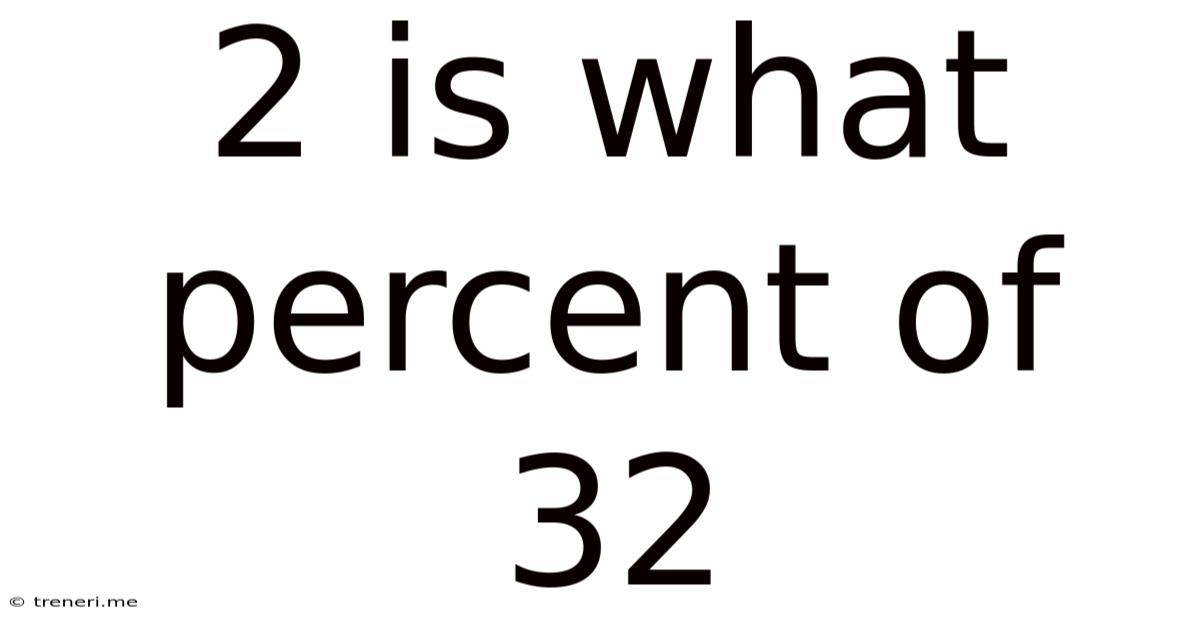
Table of Contents
2 is What Percent of 32? A Deep Dive into Percentages and Their Applications
This seemingly simple question, "2 is what percent of 32?", opens the door to a broader understanding of percentages, their calculations, and their widespread applications in various fields. While the answer itself is straightforward, exploring the underlying concepts and practical uses enhances our mathematical literacy and problem-solving skills.
Understanding Percentages: The Basics
A percentage is a way of expressing a number as a fraction of 100. The term "percent" literally means "per hundred" (from the Latin "per centum"). It's a versatile tool used to represent proportions, ratios, and changes in various contexts. Understanding percentages is crucial for everyday tasks like calculating discounts, tips, taxes, and interpreting statistical data.
Key Components of Percentage Problems
Every percentage problem involves three key components:
- The Part: This is the smaller amount that represents a fraction of the whole. In our example, "2" is the part.
- The Whole: This is the larger amount, the total quantity being considered. In our example, "32" is the whole.
- The Percentage: This is the ratio of the part to the whole, expressed as a number out of 100. This is what we need to find.
Calculating "2 is What Percent of 32?"
To solve this specific problem, we can use a simple formula:
(Part / Whole) * 100 = Percentage
Plugging in our values:
(2 / 32) * 100 = Percentage
This simplifies to:
(1 / 16) * 100 = 6.25%
Therefore, 2 is 6.25% of 32.
Different Approaches to Solving Percentage Problems
While the above formula is the most straightforward, several other methods can be employed to solve percentage problems, each offering a different perspective and potentially simplifying the calculation depending on the context.
Method 2: Using Proportions
Percentage problems can be solved using proportions. We set up a proportion where the ratio of the part to the whole is equal to the percentage over 100:
Part / Whole = Percentage / 100
Substituting our values:
2 / 32 = x / 100
Solving for x (the percentage):
x = (2 * 100) / 32 = 6.25%
This method highlights the relationship between the part, the whole, and the percentage as equivalent ratios.
Method 3: Using Decimal Equivalents
Percentages can be easily converted to decimals by dividing by 100. For example, 6.25% is equivalent to 0.0625. We can use this to solve the problem:
Whole * Decimal Equivalent = Part
32 * 0.0625 = 2
This confirms that our initial calculation is correct. This approach is particularly useful when dealing with complex percentage calculations involving multiple steps.
Practical Applications of Percentages
The ability to calculate percentages is indispensable across numerous fields. Let's explore some key areas where this skill finds practical application:
1. Finance and Business
- Profit Margins: Businesses use percentages to calculate profit margins, which is the difference between revenue and costs, expressed as a percentage of revenue.
- Interest Rates: Interest rates on loans, savings accounts, and investments are expressed as percentages. Understanding these is crucial for financial planning.
- Discounts and Sales Tax: Percentages are used extensively in retail to calculate discounts and sales tax on purchases.
- Investment Returns: Investors track their investment returns as percentages to measure the performance of their portfolio.
- Financial Statements: Percentages are widely used in financial statements (like balance sheets and income statements) to represent ratios and key performance indicators.
2. Science and Statistics
- Data Representation: Percentages are used to present data in a clear and concise manner in various scientific reports, research papers, and statistical analyses.
- Probability and Statistics: Percentages are used to express probabilities and various statistical measures. For example, expressing the likelihood of an event occurring.
- Experimental Results: In scientific experiments, percentages are commonly used to express the success rate of experiments or the relative abundance of various substances.
3. Everyday Life
- Tip Calculation: Calculating tips in restaurants and other service industries often involves percentages.
- Discount Calculation: Understanding percentages helps you take advantage of sales and discounts, saving you money.
- Understanding Surveys and Polls: Percentages are often used to represent data from surveys and polls, allowing for easy comprehension of the results.
- Nutritional Information: Nutritional information on food labels frequently uses percentages to show the percentage of daily recommended values for various nutrients.
Advanced Percentage Calculations and Concepts
Beyond basic percentage calculations, several more complex scenarios exist requiring a deeper understanding of percentages.
1. Percentage Increase and Decrease
Calculating percentage increase or decrease involves finding the difference between two values and expressing it as a percentage of the original value. For instance, if a stock price increases from $10 to $12, the percentage increase is:
((12 - 10) / 10) * 100 = 20%
Similarly, if the price decreases from $12 to $10, the percentage decrease is:
((12 - 10) / 12) * 100 ≈ 16.67%
Note that the percentage increase and decrease are not necessarily equal.
2. Compound Interest
Compound interest is the interest calculated on the initial principal, plus accumulated interest from previous periods. It's a crucial concept in finance and investing. The formula for compound interest involves percentages:
A = P (1 + r/n)^(nt)
Where:
- A = the future value of the investment/loan, including interest
- P = the principal investment amount (the initial deposit or loan amount)
- r = the annual interest rate (decimal)
- n = the number of times that interest is compounded per year
- t = the number of years the money is invested or borrowed for
3. Percentage Points
It's crucial to distinguish between percentage points and percentage change. A percentage point refers to an absolute difference between two percentages, while percentage change refers to the relative change. For example:
If interest rates rise from 5% to 8%, this is a 3-percentage-point increase. However, the percentage increase is:
((8 - 5) / 5) * 100 = 60%
This distinction is important for clear communication in financial and economic contexts.
Conclusion: Mastering Percentages for a Brighter Future
The seemingly simple question, "2 is what percent of 32?", serves as a gateway to a vast world of applications for percentages. From everyday financial decisions to complex scientific analyses, understanding and mastering percentages is a fundamental skill for navigating the modern world. By exploring various calculation methods and understanding the nuances of percentage increase, decrease, compound interest, and percentage points, individuals can enhance their mathematical literacy and make more informed decisions in various aspects of their lives. Proficiency in percentage calculations empowers individuals to analyze data effectively, make sound financial choices, and contribute meaningfully to various professional fields.
Latest Posts
Latest Posts
-
Round 43 To The Nearest Hundred
May 15, 2025
-
Cuanto Falta Para El 16 De Diciembre
May 15, 2025
-
How Much Salt In A Swimming Pool
May 15, 2025
-
What Percent Of 25 Is 24
May 15, 2025
-
How Much Hours Is 4 Days
May 15, 2025
Related Post
Thank you for visiting our website which covers about 2 Is What Percent Of 32 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.