2 Log 4 Log 2 Log 2
Treneri
May 14, 2025 · 4 min read
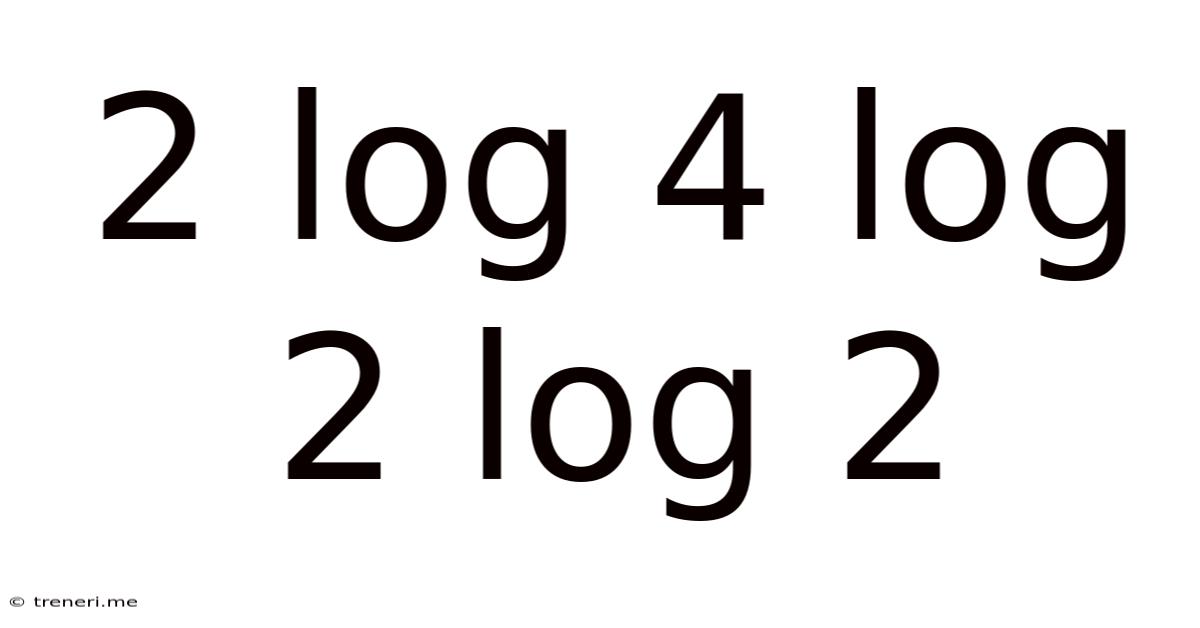
Table of Contents
Decoding the Mathematical Enigma: 2 log₄ log₂ log₂ 2
The expression "2 log₄ log₂ log₂ 2" might look intimidating at first glance, a jumble of numbers and logarithmic functions. However, with a systematic approach and understanding of logarithmic properties, we can unravel this mathematical puzzle. This article will delve deep into the solution, exploring the underlying principles of logarithms and demonstrating step-by-step how to simplify the expression. We will also discuss the importance of understanding logarithmic identities and their applications in various fields.
Understanding Logarithms: A Foundation
Before tackling the expression, let's refresh our understanding of logarithms. A logarithm is essentially the inverse operation of exponentiation. The expression log<sub>b</sub>(x) = y means that b<sup>y</sup> = x. In this notation:
- b is the base of the logarithm.
- x is the argument (the number we're taking the logarithm of).
- y is the exponent (the result of the logarithm).
For instance, log₂ 8 = 3 because 2³ = 8. The base-10 logarithm (log x) is often written without explicitly stating the base, assuming it's 10. The natural logarithm (ln x) uses the mathematical constant e (approximately 2.718) as its base.
Key Logarithmic Properties: Our Tools for Simplification
Several properties are crucial for simplifying logarithmic expressions. These properties allow us to manipulate and combine logarithmic terms efficiently. Let's review some of the most relevant properties:
- Product Rule: log<sub>b</sub>(xy) = log<sub>b</sub>(x) + log<sub>b</sub>(y)
- Quotient Rule: log<sub>b</sub>(x/y) = log<sub>b</sub>(x) - log<sub>b</sub>(y)
- Power Rule: log<sub>b</sub>(x<sup>y</sup>) = y log<sub>b</sub>(x)
- Change of Base Rule: log<sub>b</sub>(x) = log<sub>a</sub>(x) / log<sub>a</sub>(b)
- Logarithm of 1: log<sub>b</sub>(1) = 0
- Logarithm of the base: log<sub>b</sub>(b) = 1
These properties are like our tools in a toolbox; we'll select the right ones to dismantle our complex expression.
Dissecting the Expression: 2 log₄ log₂ log₂ 2
Now, let's tackle the expression: 2 log₄ log₂ log₂ 2. We will proceed step-by-step, applying the logarithmic properties where applicable.
Step 1: Innermost Logarithm
The innermost part of the expression is log₂ 2. Using the property log<sub>b</sub>(b) = 1, we find that log₂ 2 = 1. This significantly simplifies our expression:
2 log₄ log₂ (1)
Step 2: Simplifying Further
Next, we have log₂(1). Recalling the property log<sub>b</sub>(1) = 0, we get:
2 log₄ (0)
Step 3: Addressing the Challenge
Here, we encounter a significant problem. Logarithms are undefined for an argument of 0. The logarithm of zero is undefined because there is no exponent that can transform the base into zero. This is a fundamental limitation of the logarithmic function. Therefore, the expression 2 log₄ log₂ log₂ 2 is undefined.
Implications and Further Exploration
The fact that the expression is undefined highlights the importance of understanding the domain and range of logarithmic functions. It's crucial to always check for situations where the argument of the logarithm is non-positive, as this results in an undefined result. This is a common error in mathematical calculations, so careful attention to detail is essential.
Applications of Logarithms in Various Fields
Logarithms are far from merely abstract mathematical concepts. They have numerous applications in various scientific and engineering fields, including:
- Chemistry: pH calculations, which measure the acidity or alkalinity of a solution, utilize logarithms.
- Physics: Measuring sound intensity (decibels), earthquake magnitudes (Richter scale), and radioactive decay all involve logarithmic scales.
- Computer Science: Logarithmic algorithms are fundamental in efficient data searching and sorting.
- Finance: Compound interest calculations often utilize logarithmic functions.
- Signal Processing: Analyzing and manipulating signals in fields like audio and image processing frequently employs logarithmic transformations.
Advanced Logarithmic Techniques
While the initial expression was relatively straightforward, more complex logarithmic expressions might require advanced techniques, such as:
- Using Change of Base Formula: This allows us to convert between different logarithmic bases, often simplifying calculations or allowing the use of a calculator that only handles specific bases.
- Solving Logarithmic Equations: In equations involving logarithms, we can use properties to manipulate the equation, often leading to exponential equations, which can then be solved using standard techniques.
- Approximating Logarithms: For logarithms that don't have exact values, numerical approximation techniques can provide accurate estimations.
Conclusion: The Importance of Precision and Understanding
The expression 2 log₄ log₂ log₂ 2 served as a valuable exercise, illustrating the importance of careful application of logarithmic properties and an awareness of the limitations of logarithmic functions. Understanding these functions, their properties, and their limitations is crucial for anyone working with mathematical models in diverse fields. Remember, attention to detail, a solid grasp of fundamental properties, and a methodical approach are key to successfully navigating the intricacies of logarithmic expressions. The seemingly simple expression highlights the profound power and potential pitfalls of working with logarithmic functions, underscoring the need for accuracy and understanding in all mathematical endeavors.
Latest Posts
Latest Posts
-
Greatest Common Factor Of 6 And 21
May 14, 2025
-
How Many Microns In A Mil
May 14, 2025
-
What Is 3 Percent Of 60
May 14, 2025
-
1 079 Rounded To The Nearest Hundredth
May 14, 2025
-
Circumference Of A Circle With A Radius Of 6
May 14, 2025
Related Post
Thank you for visiting our website which covers about 2 Log 4 Log 2 Log 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.