2 Out Of 36 As A Percentage
Treneri
May 14, 2025 · 5 min read
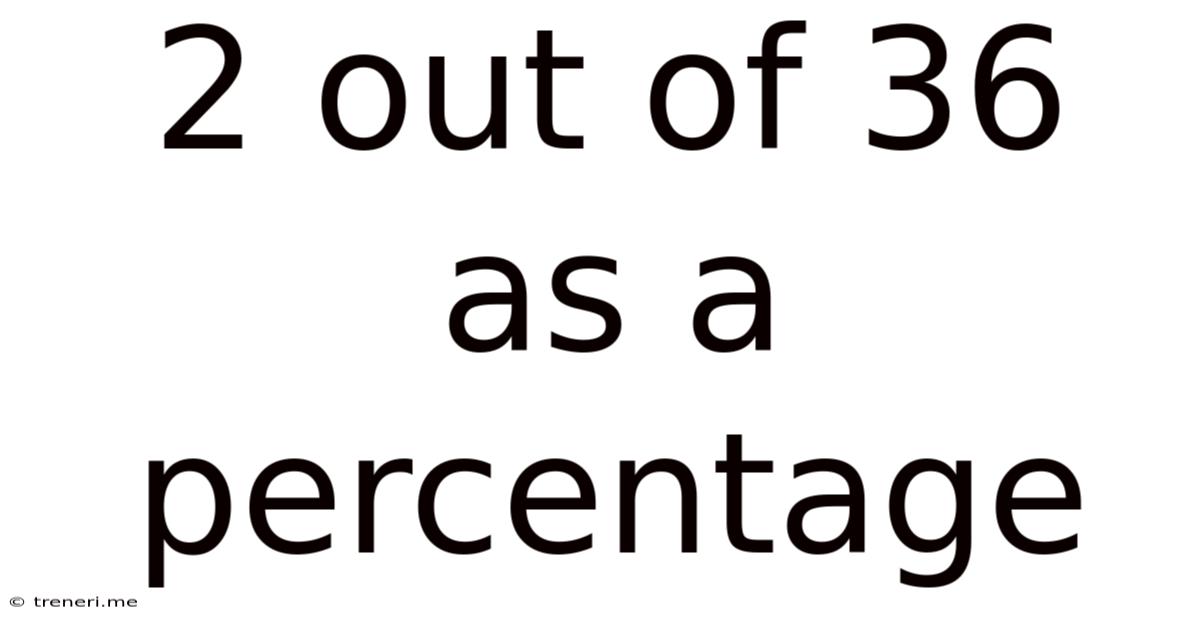
Table of Contents
2 out of 36 as a Percentage: A Comprehensive Guide
Calculating percentages is a fundamental skill applicable across numerous fields, from everyday budgeting to complex scientific analyses. Understanding how to convert fractions into percentages is crucial for interpreting data, making informed decisions, and effectively communicating quantitative information. This comprehensive guide will delve into the calculation of "2 out of 36 as a percentage," offering various methods, practical applications, and exploring related percentage calculations.
Understanding Percentages
Before we tackle the specific problem, let's establish a firm understanding of percentages. A percentage represents a fraction of 100. The word "percent" itself is derived from the Latin "per centum," meaning "out of one hundred." Therefore, any percentage can be expressed as a fraction with a denominator of 100. For example, 25% is equivalent to 25/100, which simplifies to 1/4.
Calculating 2 out of 36 as a Percentage: Method 1 - The Fraction Approach
The most straightforward way to calculate 2 out of 36 as a percentage involves expressing the ratio as a fraction and then converting it to a percentage.
-
Express as a Fraction: The phrase "2 out of 36" translates directly to the fraction 2/36.
-
Simplify the Fraction: To make the calculation easier, we simplify the fraction by finding the greatest common divisor (GCD) of the numerator (2) and the denominator (36). The GCD of 2 and 36 is 2. Dividing both the numerator and denominator by 2, we get 1/18.
-
Convert to a Decimal: To convert the fraction 1/18 to a decimal, we divide the numerator (1) by the denominator (18). This gives us 0.05555... (the 5 repeats infinitely).
-
Convert to a Percentage: To convert the decimal to a percentage, we multiply by 100 and add the percent sign (%). Therefore, 0.05555... * 100 ≈ 5.56%.
Therefore, 2 out of 36 is approximately 5.56%. The slight rounding is due to the repeating decimal.
Calculating 2 out of 36 as a Percentage: Method 2 - The Proportion Approach
Another method involves setting up a proportion. We know that a percentage is a ratio out of 100. We can set up the proportion:
2/36 = x/100
Where 'x' represents the percentage we are trying to find.
To solve for 'x', we cross-multiply:
36x = 200
Now, divide both sides by 36:
x = 200/36 ≈ 5.56
Therefore, using the proportion method, we again arrive at approximately 5.56%.
Practical Applications: Understanding the Context
The percentage 5.56% can have various interpretations depending on the context. Consider these examples:
-
Test Scores: If a student answered 2 out of 36 questions correctly on a test, their score is approximately 5.56%. This highlights a significant need for improvement.
-
Manufacturing Defects: If a manufacturing process yields 2 defective items out of 36 produced, the defect rate is about 5.56%. This indicates a relatively low but potentially concerning defect rate that might warrant investigation.
-
Survey Results: If 2 out of 36 respondents answered "yes" to a survey question, 5.56% of respondents provided an affirmative response. This data point needs to be considered within the larger context of the survey results.
-
Sales Figures: If a salesperson made 2 sales out of 36 attempts, their success rate is approximately 5.56%. This might indicate a need for improved sales techniques or targeting.
The importance of understanding the context underscores the need for careful interpretation of percentage calculations. A low percentage doesn't automatically signal failure or inadequacy; it depends heavily on the specific scenario.
Related Percentage Calculations: Expanding Your Skills
Mastering the calculation of "2 out of 36 as a percentage" lays the groundwork for understanding more complex percentage problems. Here are some related calculations you might encounter:
-
Calculating the percentage of something remaining: If 2 items are defective out of 36, then 34 items (36 - 2) are not defective. The percentage of non-defective items is 34/36 * 100 ≈ 94.44%.
-
Increasing or Decreasing a Percentage: Suppose you want to increase a value by 5.56%. If the initial value is 100, an increase of 5.56% would result in 105.56. Conversely, a decrease of 5.56% from 100 would result in 94.44.
-
Calculating Percentages of Larger Numbers: Applying the same principles, you can calculate percentages for much larger datasets. For instance, if you have 200 defective items out of 3600 produced, the defect rate is still approximately 5.56% (200/3600 * 100 ≈ 5.56%). The underlying proportion remains consistent.
-
Working with Percentages in Real-World Scenarios: Percentage calculations are integral to various real-world applications such as calculating discounts, determining tax amounts, understanding interest rates, and analyzing financial statements.
Beyond the Basics: Advanced Percentage Concepts
While the core concepts discussed above provide a solid foundation, mastering percentages involves delving deeper into more sophisticated calculations. These might include:
-
Compound Interest: Compound interest involves earning interest not only on the principal amount but also on accumulated interest. This results in exponential growth over time.
-
Percentage Change: Calculating the percentage change between two values reveals the relative increase or decrease. The formula is: [(New Value - Old Value) / Old Value] * 100.
-
Percentage Points: It’s important to distinguish between percentage change and percentage points. Percentage points refer to the arithmetic difference between two percentages, while percentage change refers to the relative difference.
-
Weighted Averages: When dealing with different weights or proportions, weighted averages are used to calculate a representative value.
-
Statistical Analysis: Percentages play a critical role in statistical analysis, including hypothesis testing and confidence intervals.
Conclusion: Mastering Percentage Calculations for Success
The ability to accurately calculate percentages is a critical skill for personal and professional success. Understanding how to convert fractions to percentages, utilizing different calculation methods, and interpreting results within the appropriate context are vital. This guide has provided a comprehensive overview, from basic calculations to more advanced concepts, empowering you to confidently tackle various percentage-related problems. Remember to always check your work and ensure your answers are logical within the given context. By continuing to practice and explore related applications, you will further hone your skills and build a strong foundation in quantitative analysis. The seemingly simple calculation of "2 out of 36 as a percentage" serves as a gateway to a broader understanding of the versatile and powerful world of percentages.
Latest Posts
Latest Posts
-
Greatest Common Factor For 9 And 15
May 14, 2025
-
How Much Is 35 Ml In Tablespoons
May 14, 2025
-
How Many Days Is A Mare Pregnant
May 14, 2025
-
Garlic Powder To Minced Garlic Conversion
May 14, 2025
-
205 321 To The Nearest Ten Thousand
May 14, 2025
Related Post
Thank you for visiting our website which covers about 2 Out Of 36 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.