2 Root 2 Plus 2 Root 2
Treneri
May 11, 2025 · 6 min read
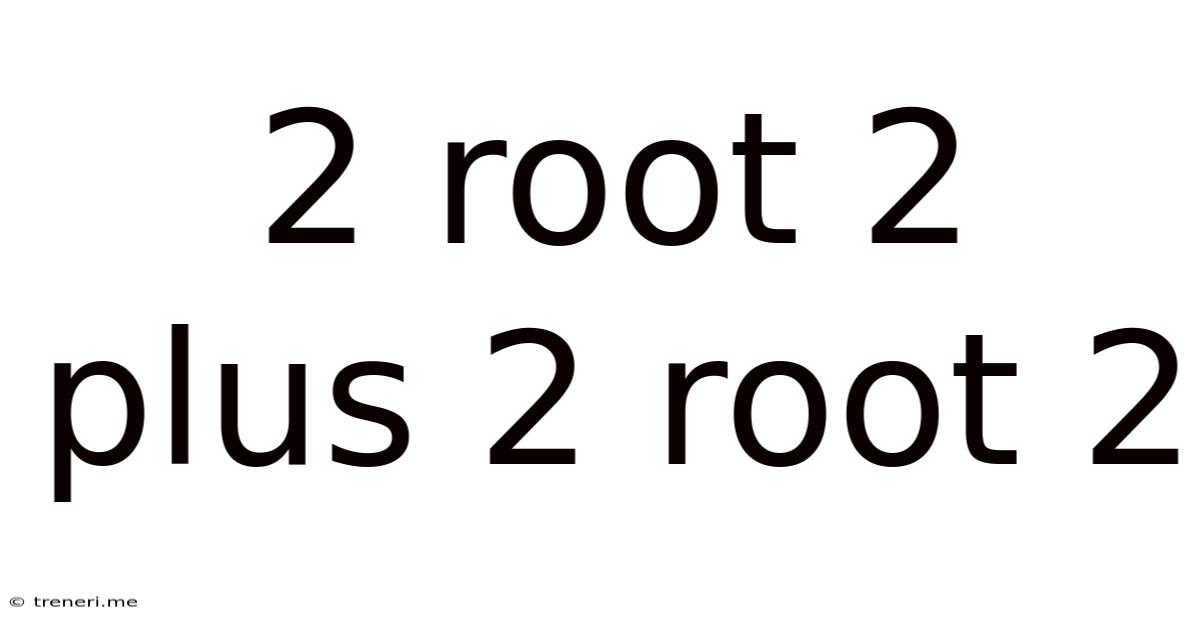
Table of Contents
2√2 + 2√2: Exploring the Simplicity and Significance of Radical Expressions
The seemingly simple mathematical expression, 2√2 + 2√2, offers a fascinating entry point into the world of radical expressions, their properties, and their applications across various fields. While the solution itself is straightforward, understanding the underlying principles involved reveals deeper insights into algebraic manipulation and the beauty of mathematical consistency. This article delves into a comprehensive exploration of this expression, dissecting its components, illustrating its simplification, and highlighting its relevance within a broader mathematical context.
Understanding the Components: Radicals and Coefficients
Before tackling the summation, let's break down the individual elements of the expression: 2√2. This is a radical expression, consisting of two primary components:
1. The Radical (√):
The symbol "√" represents a square root. A square root of a number is a value that, when multiplied by itself, equals the original number. For instance, the square root of 9 (√9) is 3, because 3 x 3 = 9. In our expression, the radical applies to the number 2.
2. The Radicand (2):
The number under the radical symbol is called the radicand. In our case, the radicand is 2. This means we are looking for a number that, when multiplied by itself, equals 2. This value is irrational, meaning it cannot be expressed as a simple fraction; its decimal representation continues infinitely without repeating.
3. The Coefficient (2):
The number preceding the radical (in this case, 2) is the coefficient. It indicates that we are dealing with two instances of √2. Therefore, 2√2 signifies two times the square root of 2.
Simplifying the Expression: 2√2 + 2√2
Now, let's address the addition: 2√2 + 2√2. This is a straightforward algebraic simplification involving like terms. Like terms in algebra are terms that have the same variable raised to the same power. In this case, both terms share the same radical expression, √2. This allows for a direct addition of the coefficients.
The simplification process is as follows:
2√2 + 2√2 = (2 + 2)√2 = 4√2
This means that the sum of 2√2 and 2√2 is equal to 4√2. The process showcases a fundamental principle of algebra: combining like terms by adding their coefficients while maintaining the common variable or radical expression.
Exploring the Value: The Irrationality of 4√2
The simplified expression, 4√2, is still an irrational number. This means its decimal representation is non-terminating and non-repeating. While we can approximate its value using a calculator (approximately 5.65685), we cannot express it precisely as a fraction or a finite decimal. This irrationality is inherent to the square root of 2, a foundational concept in mathematics and geometry.
The irrationality of √2 was famously proven by the ancient Greeks, demonstrating that not all numbers can be expressed as ratios of integers. This discovery had profound implications for the understanding of numbers and geometry. The expression 4√2 serves as a simple yet potent reminder of this fundamental mathematical concept.
Applications and Significance in Different Fields
While seemingly basic, the concept of simplifying radical expressions like 2√2 + 2√2, and understanding the nature of irrational numbers, has far-reaching applications across various fields:
1. Geometry and Trigonometry:
The square root of 2 frequently appears in geometric calculations, particularly when dealing with right-angled triangles and the Pythagorean theorem. For instance, the diagonal of a square with sides of length 1 is √2. Calculations involving diagonals, areas, and volumes of geometric shapes often involve radical expressions, necessitating the ability to simplify and manipulate them effectively. Understanding the simplification of 2√2 + 2√2 is directly applicable in such contexts.
2. Physics and Engineering:
Many physical phenomena and engineering calculations involve irrational numbers. From calculating the trajectory of projectiles to designing structural components, the ability to handle and simplify radical expressions is crucial for accuracy and efficiency. For example, in calculations involving vectors and forces, the resultant vector's magnitude might involve irrational numbers.
3. Computer Science and Programming:
While computers deal with approximations of irrational numbers, the underlying mathematical principles remain important. Computer graphics, game development, and simulations often require accurate calculations involving radical expressions. Programming algorithms for these applications must be able to handle irrational numbers efficiently.
4. Advanced Mathematics:
In advanced mathematical fields like calculus, real analysis, and linear algebra, the concepts of irrational numbers and radical expressions form the basis for more complex mathematical structures and theories. The seemingly simple addition we explored here lays the groundwork for deeper mathematical understanding.
Beyond the Basics: Expanding the Concept
The expression 2√2 + 2√2 provides a solid foundation for exploring more complex concepts:
1. Operations with Radicals:
The simplification of 2√2 + 2√2 illustrates the fundamental principle of combining like terms. This principle extends to other operations with radicals such as subtraction, multiplication, and division. Understanding how to perform these operations with different coefficients and radicands is essential for manipulating more complex radical expressions.
2. Rationalization of Denominators:
When a radical expression appears in the denominator of a fraction, it is often necessary to rationalize the denominator. This involves multiplying the numerator and denominator by a suitable expression to remove the radical from the denominator. This process is vital for simplifying expressions and ensuring consistency in mathematical calculations.
3. Solving Equations Involving Radicals:
Radical expressions often appear in equations that require solving for an unknown variable. Solving such equations typically involves isolating the radical term and then squaring both sides of the equation to eliminate the radical. It's crucial to check solutions to ensure they are valid, as the squaring process can sometimes introduce extraneous solutions.
4. Approximating Irrational Numbers:
While we often use decimal approximations for irrational numbers, understanding how to obtain accurate approximations is crucial, especially in applications where precision is paramount. Techniques like Taylor series expansions can provide efficient ways to approximate the values of irrational numbers to a desired level of accuracy.
Conclusion: The Enduring Relevance of 2√2 + 2√2
The seemingly straightforward expression, 2√2 + 2√2, serves as a gateway to a deeper appreciation of the intricacies of mathematics. Its simplification not only highlights the basic principles of algebra but also touches upon fundamental concepts such as irrational numbers, radical expressions, and their applications across various disciplines. Mastering the manipulation of radical expressions, like those exemplified in this simple addition, is essential for success in mathematics and its numerous applications in the real world. The seemingly simple problem underscores the power of mathematical principles and their far-reaching consequences. From the ancient Greeks' contemplation of the irrationality of √2 to modern-day applications in technology and engineering, this foundational concept continues to hold significance, demonstrating the enduring relevance of even the most basic mathematical principles. Understanding the simplification of 2√2 + 2√2, therefore, is not merely about arriving at the answer 4√2; it's about grasping the underlying mathematical elegance and the enduring power of these fundamental concepts.
Latest Posts
Latest Posts
-
How Much Backing Do I Need For A Quilt
May 11, 2025
-
How Many Hours Till 4 30 Pm
May 11, 2025
-
What Is The Reciprocal Of 1 8
May 11, 2025
-
How Many Years From 1970 To 2023
May 11, 2025
-
Greatest Common Factor Of 56 And 72
May 11, 2025
Related Post
Thank you for visiting our website which covers about 2 Root 2 Plus 2 Root 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.