20 Divided By 3 With Remainder
Treneri
May 14, 2025 · 5 min read
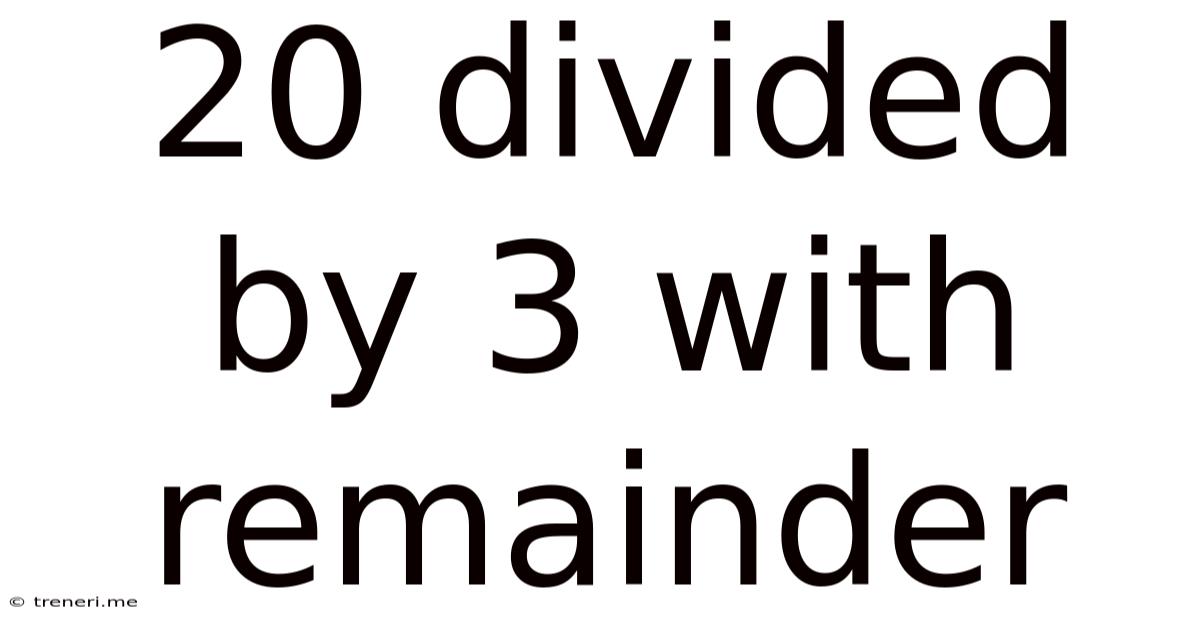
Table of Contents
20 Divided by 3 with Remainder: A Deep Dive into Division and Modular Arithmetic
The seemingly simple question, "What is 20 divided by 3 with remainder?" opens a door to a fascinating world of mathematical concepts. While the immediate answer might seem obvious to many, exploring this problem delves into fundamental principles of division, introduces the concept of modular arithmetic, and reveals its practical applications across various fields. This comprehensive guide will dissect this problem, exploring its various facets and showcasing its significance in mathematics and beyond.
Understanding Division and Remainders
Division is a fundamental arithmetic operation that involves splitting a quantity into equal parts. When we divide a number (the dividend) by another number (the divisor), we obtain a quotient and potentially a remainder. The quotient represents how many times the divisor fits entirely into the dividend, while the remainder represents the amount left over after the division.
In the case of 20 divided by 3, we can express the process as:
20 ÷ 3 = 6 with a remainder of 2
This means that 3 fits into 20 six times (6 x 3 = 18), leaving a remainder of 2 (20 - 18 = 2). This can be represented using the division algorithm:
Dividend = (Quotient x Divisor) + Remainder
Therefore, 20 = (6 x 3) + 2
The Significance of Remainders
Remainders are not simply leftover numbers; they carry significant mathematical meaning. They provide crucial information about the relationship between the dividend and the divisor. Understanding remainders is fundamental in various mathematical operations and concepts, including:
1. Modular Arithmetic (Clock Arithmetic)
Modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" upon reaching a certain value—the modulus. Think of a clock: when the hour hand reaches 12, it resets to 1. This is modular arithmetic with a modulus of 12.
In our example, 20 divided by 3 with a remainder of 2 can be expressed using modular arithmetic as:
20 ≡ 2 (mod 3)
This reads as "20 is congruent to 2 modulo 3," meaning that 20 and 2 leave the same remainder when divided by 3.
Modular arithmetic has numerous applications, including:
- Cryptography: Used extensively in secure communication systems to encrypt and decrypt data.
- Computer Science: Used in hashing algorithms, data structures, and error detection.
- Number Theory: Forms the basis for many number-theoretic concepts and proofs.
2. Identifying Even and Odd Numbers
Remainders can easily identify even and odd numbers. An even number has a remainder of 0 when divided by 2, while an odd number has a remainder of 1.
3. Determining Divisibility Rules
Divisibility rules rely heavily on remainders. For example, a number is divisible by 3 if the sum of its digits is divisible by 3. This rule is directly related to the remainders obtained when dividing the number and the sum of its digits by 3.
4. Solving Problems Involving Grouping and Sharing
Many real-world problems involve dividing quantities into groups or sharing items among individuals. Remainders provide crucial information about how many items are left over after equal distribution. For example, if you have 20 candies to distribute among 3 friends, each friend will receive 6 candies, and you'll have 2 candies left over.
Exploring Different Methods to Find the Remainder
While long division is the most common method, there are other approaches to find the remainder when dividing 20 by 3:
1. Repeated Subtraction
Repeatedly subtract the divisor (3) from the dividend (20) until the result is less than the divisor. The final result is the remainder.
20 - 3 = 17 17 - 3 = 14 14 - 3 = 11 11 - 3 = 8 8 - 3 = 5 5 - 3 = 2
The remainder is 2.
2. Using a Calculator
Most calculators can perform division and display the quotient and remainder. However, the method of displaying the remainder might vary depending on the calculator model.
3. Modular Arithmetic Formula
The remainder can be calculated directly using the modular arithmetic congruence:
20 mod 3 = 2
This is often represented by the modulo operator (%) in programming languages.
Advanced Applications of Remainders
The seemingly simple concept of remainders extends to more advanced mathematical concepts:
1. The Euclidean Algorithm
The Euclidean algorithm is a method for finding the greatest common divisor (GCD) of two integers. This algorithm relies heavily on repeated application of the division algorithm and the analysis of remainders.
2. Congruence Classes
In modular arithmetic, numbers with the same remainder when divided by a given modulus belong to the same congruence class. For instance, in modulo 3, the numbers 2, 5, 8, 11, 14, 17, 20... all belong to the same congruence class because they all leave a remainder of 2 when divided by 3.
3. Fermat's Little Theorem
This theorem in number theory deals with congruences and remainders, providing a powerful tool in modular arithmetic and cryptography.
Real-World Examples
The concept of division with remainder has wide-ranging applications:
- Scheduling: Determining the number of shifts needed and any leftover shifts in a weekly schedule.
- Inventory Management: Calculating the number of full boxes and any remaining items in a warehouse.
- Resource Allocation: Distributing resources (e.g., funds, materials) fairly among individuals or teams.
- Computer Programming: Implementing modular arithmetic functions and algorithms.
Conclusion
The seemingly simple problem of 20 divided by 3 with a remainder opens the door to a rich landscape of mathematical concepts, from the fundamental principles of division to the sophisticated applications of modular arithmetic and beyond. Understanding remainders is crucial not only for solving basic arithmetic problems but also for tackling complex mathematical challenges and real-world scenarios across diverse fields. The significance of remainders extends far beyond simple leftover numbers; they provide valuable insights into the relationships between numbers and unlock a world of possibilities in mathematics and its applications. This exploration should encourage deeper inquiry into the beauty and power of mathematical concepts seemingly simple at first glance.
Latest Posts
Latest Posts
-
How Many Drapery Panels Do I Need
May 14, 2025
-
What Is The Gcf Of 54 And 24
May 14, 2025
-
How Long Would It Take To Travel 40 Light Years
May 14, 2025
-
Cuanto Es 1 Ano En Horas
May 14, 2025
-
How To Find Area Of A Triangle With Points
May 14, 2025
Related Post
Thank you for visiting our website which covers about 20 Divided By 3 With Remainder . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.