20 Is What Percent Of 150
Treneri
May 15, 2025 · 4 min read
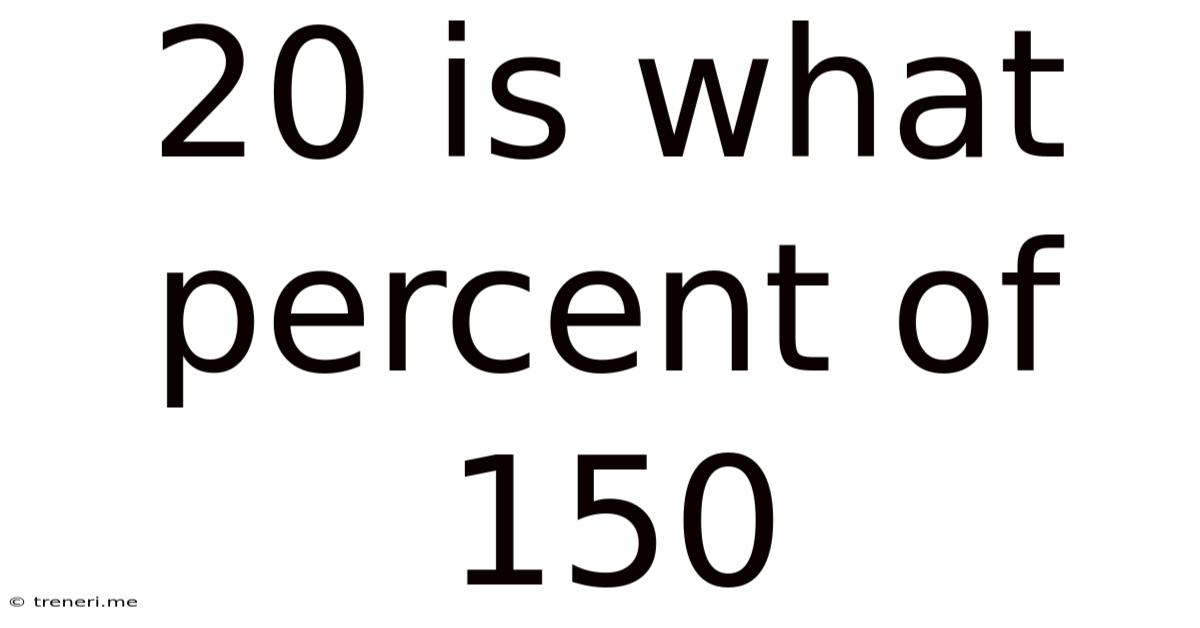
Table of Contents
20 is What Percent of 150? A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill in various aspects of life, from calculating discounts and taxes to analyzing data and understanding financial reports. This article dives deep into the question, "20 is what percent of 150?", providing a step-by-step solution, exploring different calculation methods, and offering practical applications to solidify your understanding of percentages.
Understanding Percentages
Before tackling the specific problem, let's refresh our understanding of percentages. A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" represents "percent," meaning "out of 100." For example, 50% means 50 out of 100, which simplifies to 1/2 or 0.5.
Calculating "20 is What Percent of 150?" – Method 1: The Formula Approach
The most straightforward way to solve this problem is using the basic percentage formula:
(Part / Whole) x 100 = Percentage
In this case:
- Part: 20
- Whole: 150
Substituting these values into the formula:
(20 / 150) x 100 = Percentage
-
Divide the part by the whole: 20 / 150 = 0.13333...
-
Multiply the result by 100: 0.13333... x 100 = 13.333...
Therefore, 20 is approximately 13.33% of 150.
Calculating "20 is What Percent of 150?" – Method 2: Using Proportions
Another effective approach involves setting up a proportion:
x/100 = 20/150
Where 'x' represents the percentage we want to find.
To solve for 'x', we cross-multiply:
150x = 2000
Then, divide both sides by 150:
x = 2000 / 150
x = 13.333...
Again, we arrive at the answer: 20 is approximately 13.33% of 150.
Understanding the Result: Context and Application
The result, 13.33%, signifies that 20 represents approximately one-eighth of 150. This percentage calculation has numerous real-world applications:
-
Sales and Discounts: If a store offers a discount of 13.33% on an item originally priced at $150, the discount amount would be $20, bringing the final price down to $130.
-
Data Analysis: In statistical analysis, percentages are crucial for presenting data proportionally. For example, if 20 out of 150 participants in a survey responded positively, this would represent a 13.33% positive response rate.
-
Financial Calculations: Percentages are essential for understanding interest rates, profit margins, and investment returns. For instance, if an investment of $150 yields a profit of $20, the return on investment would be 13.33%.
-
Grade Calculation: If a student scores 20 out of 150 points on a test, their grade would be approximately 13.33%.
Rounding and Precision
Notice that our result includes repeating decimal places (13.333...). In practical scenarios, you'll often need to round the percentage to a specific level of precision. The level of precision depends on the context:
-
For general purposes: Rounding to one decimal place (13.3%) is usually sufficient.
-
For financial calculations: Rounding to two decimal places (13.33%) or even more, might be necessary for accuracy.
Always consider the level of precision required for your specific situation.
Further Exploration: Inverse Percentage Calculations
Understanding the relationship between percentages, parts, and wholes allows us to solve inverse problems as well. For instance, if we know that 13.33% of a number is 20, we can find the original number using the formula:
Whole = (Part / Percentage) x 100
Therefore, (20 / 13.33) x 100 = approximately 150.
Percentage Calculation Tools and Resources
While manual calculations are valuable for understanding the underlying principles, numerous online calculators and spreadsheet software (like Microsoft Excel or Google Sheets) can simplify percentage calculations. These tools are especially helpful when dealing with more complex scenarios or a large volume of calculations.
Practical Exercises: Test Your Understanding
To reinforce your understanding, try solving these related percentage problems:
- What is 30% of 250?
- 15 is what percent of 75?
- If a store offers a 25% discount on an item priced at $120, what is the final price after the discount?
- A student scored 80 out of 100 on a test. What is their percentage score?
- If a company's profit is $50,000 and its revenue is $200,000, what is the profit margin as a percentage?
By working through these examples, you can further strengthen your ability to perform and interpret percentage calculations in various real-world contexts.
Conclusion: Mastering Percentage Calculations
Mastering percentage calculations is a valuable skill that enhances your problem-solving abilities across numerous disciplines. By understanding the fundamental formula, utilizing different calculation methods, and practicing regularly, you'll be able to confidently tackle percentage problems and leverage this knowledge in your personal and professional life. Remember to always consider the context and choose the appropriate level of precision when rounding your results. This comprehensive guide provides a solid foundation for understanding and applying percentages effectively. Now go forth and conquer those percentage challenges!
Latest Posts
Latest Posts
-
Write 72 As A Fraction In Simplest Form
May 15, 2025
-
100 Ml Milk Is How Many Cups
May 15, 2025
-
Find The Radius Of A Circle Circumscribed About A Triangle
May 15, 2025
-
602 88 Rounded To The Nearest Tenth
May 15, 2025
-
How Long Is 32 Months In Years
May 15, 2025
Related Post
Thank you for visiting our website which covers about 20 Is What Percent Of 150 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.