20 Out Of 36 As A Percentage
Treneri
May 12, 2025 · 5 min read
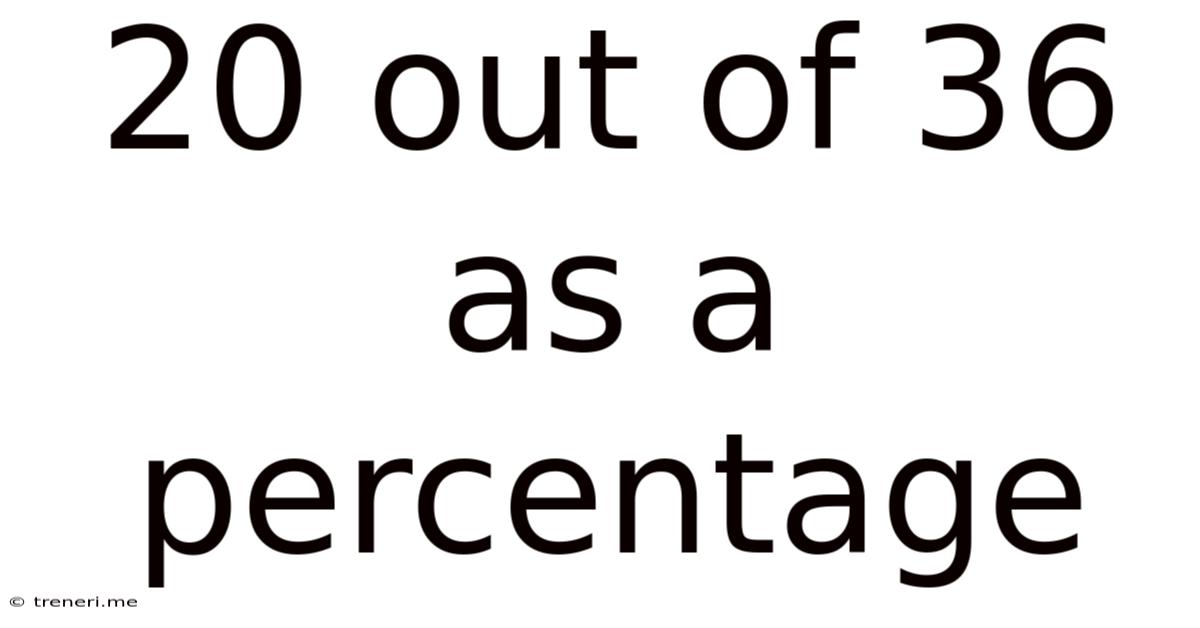
Table of Contents
20 out of 36 as a Percentage: A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill applicable across numerous fields, from everyday finances to complex scientific analyses. This comprehensive guide delves into calculating percentages, focusing specifically on determining what 20 out of 36 represents as a percentage, and then expanding to broader applications and practical examples. We'll explore various methods, providing clear explanations and practical tips to solidify your understanding.
Understanding the Basics of Percentages
A percentage represents a fraction of 100. It expresses a proportion or a rate per hundred. The symbol "%" denotes percentage. For example, 50% means 50 out of 100, or one-half. The core concept involves relating a part to a whole, expressing that relationship as a fraction of 100.
Calculating 20 out of 36 as a Percentage: The Step-by-Step Approach
To determine what 20 out of 36 represents as a percentage, we follow these straightforward steps:
-
Form a Fraction: Express the relationship as a fraction: 20/36. This signifies the part (20) compared to the whole (36).
-
Convert to Decimal: Divide the numerator (20) by the denominator (36): 20 ÷ 36 ≈ 0.5556.
-
Convert to Percentage: Multiply the decimal by 100: 0.5556 x 100 ≈ 55.56%.
Therefore, 20 out of 36 is approximately 55.56%.
Alternative Calculation Methods
While the above method is the most common, other approaches exist, each offering a slightly different perspective:
-
Using Proportions: Set up a proportion: 20/36 = x/100. Solving for 'x' yields the percentage. Cross-multiply: 20 * 100 = 36 * x. Then, divide both sides by 36: x = (20 * 100) / 36 ≈ 55.56%.
-
Simplifying the Fraction: Before converting to a decimal, simplify the fraction 20/36. Both numerator and denominator are divisible by 4, resulting in 5/9. Then, divide 5 by 9 (≈ 0.5556) and multiply by 100 to get the percentage (≈ 55.56%). Simplifying first can sometimes make the calculation easier, particularly with larger numbers.
Rounding Percentages
In many instances, you'll need to round percentages to a specific number of decimal places. For example, 55.56% might be rounded to 55.6% or 56%, depending on the context and required precision. Rounding rules dictate that if the digit following the rounding place is 5 or greater, you round up; otherwise, you round down.
Practical Applications of Percentage Calculations
Percentage calculations are ubiquitous in everyday life:
-
Grades and Scores: Calculating your grade on a test or assignment involves determining the percentage of correct answers. For instance, if you answered 18 questions correctly out of 25, your percentage score would be (18/25) * 100 = 72%.
-
Discounts and Sales: Retail stores frequently advertise discounts as percentages. A 20% discount on a $100 item means you'll pay $80 ($100 - ($100 * 0.20)).
-
Taxes: Sales tax, income tax, and other taxes are often expressed as percentages of the base amount.
-
Tips and Gratuities: Calculating a tip in a restaurant involves determining a percentage of the bill. A 15% tip on a $50 meal is $7.50 ($50 * 0.15).
-
Interest Rates: Interest rates on loans and savings accounts are expressed as percentages.
-
Financial Analysis: Percentage changes are crucial for analyzing financial data, such as comparing year-over-year revenue growth or understanding stock market fluctuations. For example, if a company's revenue increased from $1 million to $1.2 million, the percentage increase is ((1.2 - 1) / 1) * 100 = 20%.
-
Science and Statistics: Percentages are fundamental in statistical analysis, representing probabilities, proportions within populations, and error margins.
-
Data Visualization: Charts and graphs often use percentages to present data clearly and concisely. Pie charts, for instance, visually represent percentages of a whole.
Beyond the Basics: Advanced Percentage Calculations
While calculating 20 out of 36 as a percentage is relatively straightforward, more complex scenarios might require a deeper understanding:
-
Percentage Increase/Decrease: Determining the percentage change between two values involves calculating the difference between the two values, dividing by the original value, and then multiplying by 100.
-
Finding the Original Value: If you know the final value after a percentage increase or decrease, you can work backward to find the original value. This often requires algebraic manipulation.
-
Compound Interest: Compound interest calculations involve applying interest to the principal amount plus accumulated interest over time, leading to exponential growth.
-
Percentage Points: It's important to distinguish between percentage points and percentages. A change from 20% to 25% is a 5 percentage point increase, but a 25% increase relative to the original 20%.
Using Technology for Percentage Calculations
Many tools can assist with percentage calculations, streamlining the process:
-
Calculators: Most calculators have a percentage function, simplifying the calculation significantly.
-
Spreadsheets: Spreadsheet software (like Microsoft Excel or Google Sheets) allows for efficient percentage calculations, especially with large datasets. Built-in functions like
=PERCENTAGE(numerator, denominator)can handle complex calculations with ease. -
Online Percentage Calculators: Numerous online calculators are specifically designed for percentage calculations, providing an easy-to-use interface for various scenarios.
Mastering Percentages: Tips and Practice
To truly master percentage calculations, consistent practice is key. Start with simple examples and gradually progress to more complex ones. Focus on understanding the underlying principles, not just memorizing formulas. Use various methods to solve problems, comparing results to ensure accuracy. Finally, consider applying your knowledge to real-world scenarios to solidify your understanding and make the learning process more engaging.
By understanding the fundamental principles of percentage calculations and practicing regularly, you'll confidently tackle any percentage-related problem, from the simple (like 20 out of 36) to the more complex. This comprehensive guide aims to equip you with the knowledge and tools necessary to master this essential skill. Remember to always double-check your calculations and consider using technology to aid in more complex scenarios. Consistent practice and a clear understanding of the core concepts are the keys to success in mastering percentages.
Latest Posts
Latest Posts
-
What Is The Area Of This Circle In Square Centimeters
May 12, 2025
-
Expanded Form With Powers Of 10
May 12, 2025
-
How To Find Commission Rate Without Percentage
May 12, 2025
-
How Many Days Is 200 Weeks
May 12, 2025
-
Cuantos Dias Faltan Para El 9 De Enero
May 12, 2025
Related Post
Thank you for visiting our website which covers about 20 Out Of 36 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.