20 Out Of 40 As A Percentage
Treneri
May 10, 2025 · 5 min read
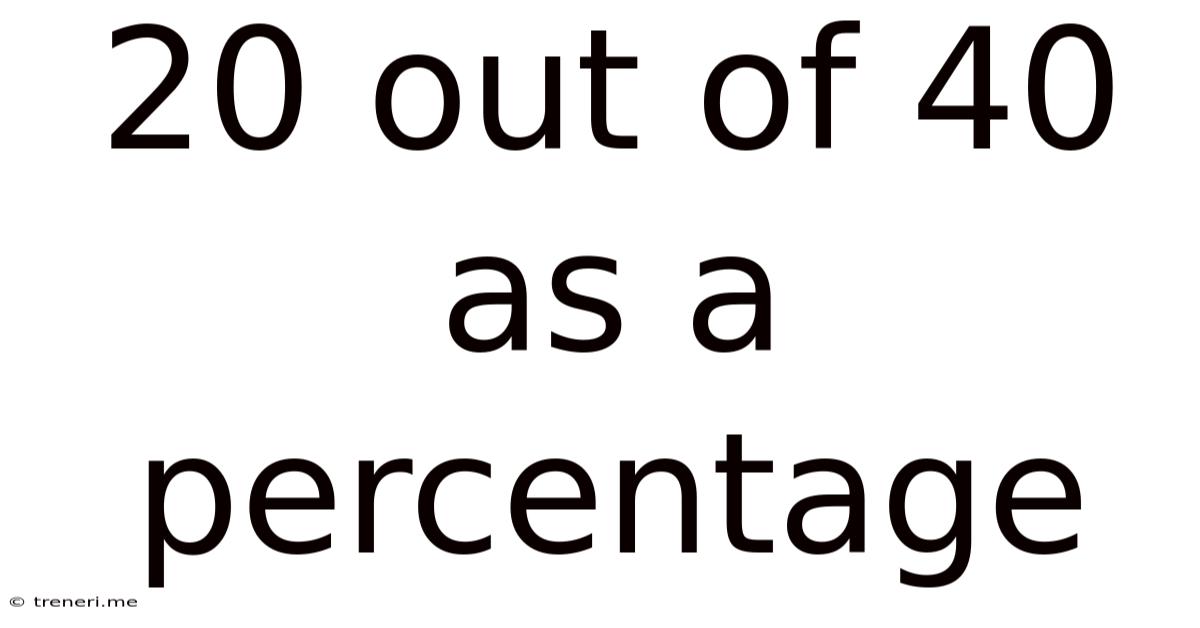
Table of Contents
20 out of 40 as a Percentage: A Comprehensive Guide
Calculating percentages is a fundamental skill applicable across various aspects of life, from academic assessments to financial transactions and everyday decision-making. Understanding how to convert fractions into percentages is crucial for interpreting data, analyzing performance, and making informed judgments. This comprehensive guide delves into the specifics of calculating "20 out of 40 as a percentage," exploring the process, its applications, and related concepts to provide a thorough understanding.
Understanding Percentages
A percentage represents a fraction or proportion out of 100. The term "percent" is derived from the Latin "per centum," meaning "out of one hundred." Percentages provide a standardized way to compare and express proportions, making them easily understandable and comparable across different contexts.
Calculating 20 out of 40 as a Percentage
The core process involves converting the fraction 20/40 into a percentage. Here's a step-by-step breakdown:
Step 1: Express as a Fraction:
The problem "20 out of 40" is directly represented as the fraction 20/40.
Step 2: Simplify the Fraction (Optional but Recommended):
Simplifying the fraction makes the calculation easier. 20/40 can be simplified by dividing both the numerator (20) and the denominator (40) by their greatest common divisor, which is 20. This simplifies the fraction to 1/2.
Step 3: Convert the Fraction to a Decimal:
To convert the simplified fraction 1/2 to a decimal, divide the numerator (1) by the denominator (2):
1 ÷ 2 = 0.5
Step 4: Convert the Decimal to a Percentage:
Multiply the decimal by 100 and add the percent symbol (%):
0.5 x 100 = 50%
Therefore, 20 out of 40 is equal to 50%.
Alternative Calculation Method: Direct Percentage Calculation
You can also calculate the percentage directly without simplifying the fraction:
(20/40) * 100% = 50%
This method yields the same result, demonstrating the flexibility in approaching percentage calculations.
Real-World Applications of Percentage Calculations
Understanding how to calculate percentages has widespread practical applications:
1. Academic Performance:
- Grade Calculation: Many grading systems use percentages to represent student performance. A score of 20 out of 40 on a test translates to a 50%, providing a clear understanding of the student's achievement.
- Class Average: Calculating the average performance of a class involves using percentages. Teachers often calculate average class scores to assess overall student understanding.
2. Financial Matters:
- Discounts: Retailers frequently offer discounts expressed as percentages. A "50% off" sale means you pay half the original price.
- Interest Rates: Interest rates on loans, savings accounts, and investments are expressed as percentages. Understanding percentage calculations is crucial for making informed financial decisions.
- Tax Calculation: Sales taxes and income taxes are calculated as percentages of the total amount.
3. Data Analysis and Statistics:
- Survey Results: Percentages are used to represent survey results and provide insights into public opinion or market trends.
- Data Representation: Graphs and charts often use percentages to visualize data proportions, making complex information easier to understand.
4. Everyday Life:
- Tip Calculation: Calculating a tip at a restaurant often involves determining a percentage of the bill amount.
- Ingredient Ratios: Recipes frequently use percentages to express the ratios of different ingredients.
Understanding Different Percentage Ranges
It's essential to interpret percentages within their context. A 50% score is considered average, while scores above 50% represent above-average performance. However, the significance of a percentage score depends heavily on the specific context:
- High-stakes exams: A 50% score on a critical exam might be considered failing, whereas in other situations, it might be acceptable or even excellent.
- Financial investments: A 50% return on investment is usually considered very good, while a 50% loss is disastrous.
Expanding Your Understanding: Related Concepts
To build a stronger foundation in percentage calculations, let's explore some related concepts:
1. Percentage Increase and Decrease:
These concepts describe the change in a value expressed as a percentage. For example, an increase from 20 to 30 represents a 50% increase, while a decrease from 30 to 20 represents a 33.33% decrease. The calculation involves finding the difference between the new and old values, dividing by the original value, and multiplying by 100%.
2. Percentage Points:
Percentage points represent the arithmetic difference between two percentages. For example, if the interest rate increases from 5% to 10%, it has increased by 5 percentage points, not 100%. This distinction is crucial for accurate interpretation of data.
3. Fractions, Decimals, and Percentages: The Interplay
It is vital to understand the inter-relationship between these three concepts. They are all different ways of representing the same value. A fraction can be converted to a decimal by division and then to a percentage by multiplying by 100. Similarly, a percentage can be converted to a decimal by dividing by 100 and then to a fraction by simplifying the resulting decimal.
Beyond the Basics: Advanced Percentage Applications
The principles discussed above form a foundation for more complex percentage calculations and applications:
- Compound Interest: Calculating compound interest involves repeated percentage calculations over time, showcasing the power of exponential growth.
- Statistical Analysis: Percentages are frequently used in various statistical measures, including mean, median, mode, and standard deviation.
- Financial Modeling: In finance, percentage calculations are crucial for discounted cash flow analysis, net present value, and other financial modeling techniques.
Conclusion
Calculating "20 out of 40 as a percentage" provides a simple yet powerful illustration of a fundamental mathematical concept. Mastering percentage calculations enhances one's ability to interpret data, make informed decisions, and effectively communicate quantitative information across various personal and professional contexts. By understanding the underlying principles and exploring the related concepts, one can build a strong foundation for handling more complex percentage applications in the future. Remember that consistent practice and applying these concepts to real-world scenarios are key to solidifying your understanding and enhancing your problem-solving skills. As you continue to practice, you'll find that percentage calculations become intuitive and effortless, enabling you to navigate numerical information with confidence and accuracy.
Latest Posts
Latest Posts
-
1 25 Rounded To The Nearest Hundredth
May 10, 2025
-
Complete The Slope Intercept Form Of This Line Y 4x
May 10, 2025
-
Time And A Half For 16 An Hour
May 10, 2025
-
Is Iu The Same As Mg
May 10, 2025
-
How To Find Lateral Area Of A Triangular Prism
May 10, 2025
Related Post
Thank you for visiting our website which covers about 20 Out Of 40 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.