200 Is What Percent Of 120
Treneri
May 13, 2025 · 4 min read
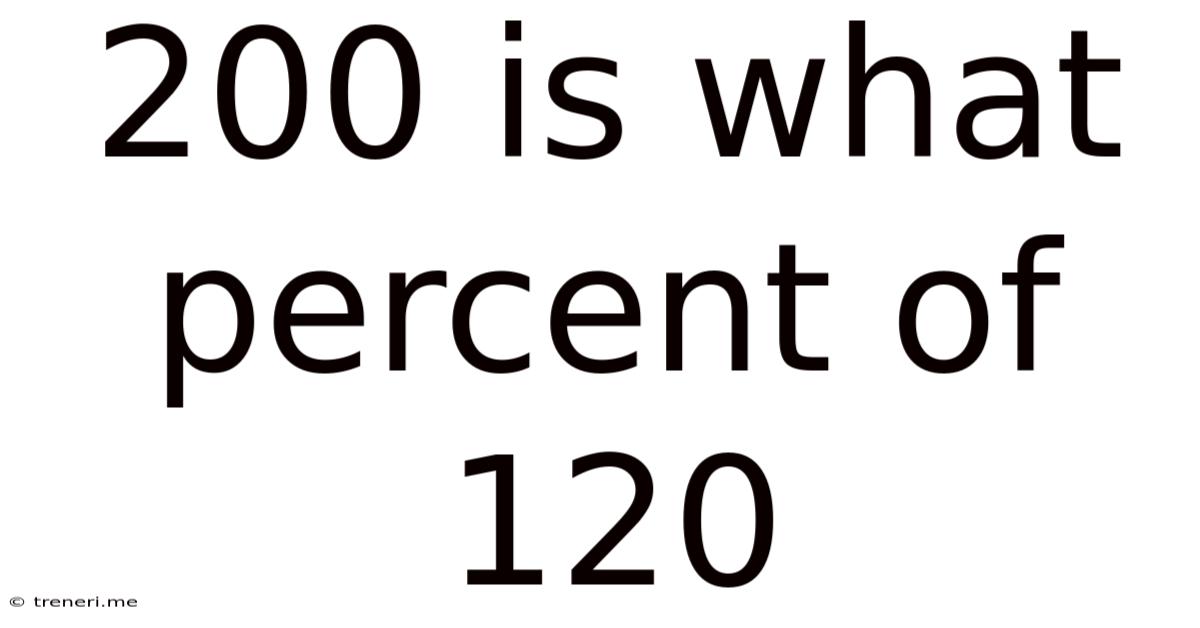
Table of Contents
200 is What Percent of 120? A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill applicable across various aspects of life, from calculating discounts and taxes to analyzing data and understanding financial reports. This article delves into the question, "200 is what percent of 120?", providing a comprehensive explanation of the calculation process, exploring different approaches, and highlighting the practical applications of percentage calculations. We will also touch upon related concepts and offer tips for mastering percentage problems.
Understanding the Basics of Percentages
Before tackling the specific problem, let's refresh our understanding of percentages. A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" represents "percent" or "per hundred." For instance, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5.
The core concept lies in expressing a part as a proportion of a whole. The whole is considered 100%, and any part is a percentage of that whole. This concept applies to various scenarios: discounts in a store, exam scores, growth rates, and more.
Calculating "200 is What Percent of 120?"
The question, "200 is what percent of 120?" is a bit counter-intuitive because the part (200) is larger than the whole (120). This indicates the result will be a percentage greater than 100%. Here's how we solve it using different methods:
Method 1: Using the Percentage Formula
The standard percentage formula is:
(Part / Whole) * 100% = Percentage
In our case:
- Part: 200
- Whole: 120
Substituting these values into the formula:
(200 / 120) * 100% = 166.67%
Therefore, 200 is 166.67% of 120. The result being greater than 100% confirms our initial observation that the part exceeds the whole.
Method 2: Setting up a Proportion
Another way to approach this problem is by setting up a proportion:
x / 100 = 200 / 120
Here, 'x' represents the percentage we're trying to find. To solve for 'x', we cross-multiply:
120x = 200 * 100
120x = 20000
x = 20000 / 120
x = 166.67%
Method 3: Using Decimal Conversion
We can also convert the fraction to a decimal and then multiply by 100%:
200 / 120 = 1.6667
1.6667 * 100% = 166.67%
Understanding the Result: Percentages Greater Than 100%
It's crucial to understand that percentages can exceed 100%. This simply indicates that the "part" is larger than the "whole." This scenario often arises when comparing changes or growth over time. For example:
- Sales Growth: If a company's sales increased from 120 units to 200 units, the growth is 166.67%.
- Population Increase: If a town's population grew from 120 to 200, the population increase is 166.67%.
- Investment Returns: If an investment of 120 dollars yielded a return of 200 dollars, the return on investment is 166.67%.
Practical Applications of Percentage Calculations
Percentage calculations are ubiquitous in various fields:
- Finance: Calculating interest rates, loan payments, investment returns, tax rates, discounts, and profit margins.
- Retail: Determining sale prices, calculating markups, analyzing sales data.
- Science: Representing experimental data, analyzing statistical results, expressing concentrations and proportions.
- Education: Grading exams, analyzing student performance, calculating GPA.
Tips for Mastering Percentage Problems
- Practice regularly: Consistent practice is key to mastering percentage calculations. Try different problem types and variations.
- Understand the concepts: Focus on grasping the core concept of percentages as a ratio out of 100.
- Use different methods: Familiarize yourself with multiple approaches (formula, proportion, decimal conversion) to solve percentage problems. This allows you to choose the method that best suits each problem.
- Check your answers: Always check your work to ensure accuracy. You can do this by reversing the calculation or using a different method to verify your result.
- Use online resources: Numerous online calculators and tutorials are available to help you practice and enhance your understanding of percentages.
Beyond the Basics: Advanced Percentage Calculations
While this article focuses on the basic percentage calculation of "200 is what percent of 120?", understanding percentages extends to more complex scenarios:
Percentage Change
Percentage change calculates the proportional change between an initial and a final value. The formula is:
[(Final Value - Initial Value) / Initial Value] * 100% = Percentage Change
For example, the percentage change from 120 to 200 is:
[(200 - 120) / 120] * 100% = 66.67% increase
Percentage Increase/Decrease
This specifically highlights whether the change represents an increase or decrease. We already touched upon this in the percentage change example above. Understanding whether a value increased or decreased is crucial for accurate interpretation.
Percentage Points
Percentage points represent the absolute difference between two percentages. For example, if the interest rate increases from 5% to 8%, the increase is 3 percentage points, not 60% (which would be the percentage change).
Conclusion
The calculation "200 is what percent of 120?" reveals that 200 represents 166.67% of 120. This highlights the versatility of percentage calculations and their applicability across numerous contexts. By understanding the fundamental principles and practicing various methods, you can confidently tackle percentage problems and apply this crucial skill to various aspects of your life and work. Remember that mastering percentages goes beyond simple calculations; it involves interpreting results, understanding context, and applying the knowledge to solve real-world problems effectively. Continual practice and exploration of more advanced concepts will further solidify your understanding and proficiency in this essential mathematical skill.
Latest Posts
Latest Posts
-
How Long Ago Was 1990 In Years
May 13, 2025
-
How Much Is 300 Mcg In Mg
May 13, 2025
-
2 Hour Half Marathon Pace Chart
May 13, 2025
-
How Many More Minutes Until 11 Am Today
May 13, 2025
-
How Much Is 2 5 Gallons In Quarts
May 13, 2025
Related Post
Thank you for visiting our website which covers about 200 Is What Percent Of 120 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.