200 Is What Percent Of 40
Treneri
May 14, 2025 · 5 min read
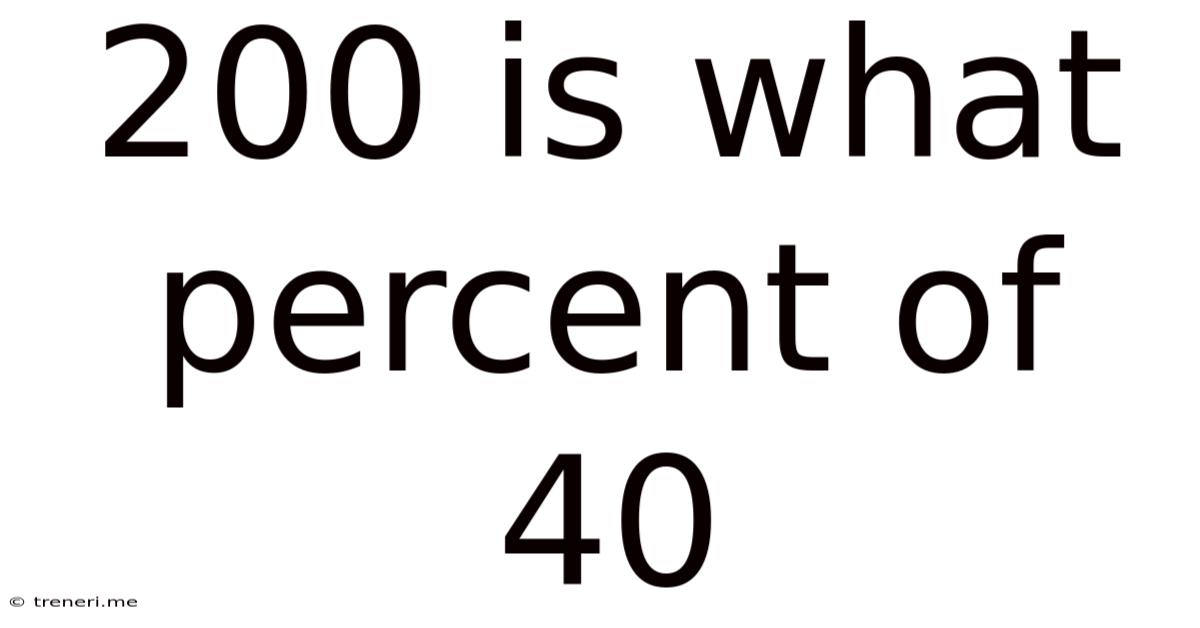
Table of Contents
200 is What Percent of 40? Understanding Percentage Calculations and Their Applications
This seemingly simple question, "200 is what percent of 40?", opens the door to understanding a fundamental mathematical concept with wide-ranging applications in various fields. While the answer might seem counterintuitive at first glance (because 200 is larger than 40), the process of solving it illuminates the mechanics of percentage calculations and their practical uses in everyday life, from calculating discounts and taxes to understanding statistical data and financial analyses. Let's delve into the solution, explore the underlying concepts, and uncover the diverse applications of percentage calculations.
Understanding Percentages: A Foundation
Before diving into the specific problem, let's establish a solid understanding of percentages. A percentage is a way of expressing a number as a fraction of 100. The word "percent" itself is derived from the Latin "per centum," meaning "out of one hundred." Therefore, 50% means 50 out of 100, or 50/100, which simplifies to 1/2 or 0.5.
Key Concepts:
- Part: This represents the number you're comparing (in our case, 200).
- Whole: This is the total number against which you're comparing the part (in our case, 40).
- Percentage: This is the fraction of the whole that the part represents, expressed as a number out of 100.
Solving the Problem: 200 is What Percent of 40?
The question "200 is what percent of 40?" can be expressed mathematically as:
x% of 40 = 200
To solve for 'x,' we need to perform the following steps:
-
Convert the percentage to a decimal: We represent 'x%' as 'x/100'.
-
Set up the equation: The equation becomes:
(x/100) * 40 = 200 -
Solve for x:
- Multiply both sides by 100:
x * 40 = 20000 - Divide both sides by 40:
x = 20000 / 40 - Simplify:
x = 500
- Multiply both sides by 100:
Therefore, 200 is 500% of 40.
This result highlights that a percentage can be greater than 100%. This simply means that the "part" (200) is more than the "whole" (40). This scenario frequently occurs in contexts involving growth, increase, or comparisons where the final value exceeds the initial value.
Practical Applications of Percentage Calculations
The ability to calculate percentages is essential in numerous real-world scenarios. Here are some key examples:
1. Finance and Budgeting:
- Interest Rates: Understanding interest rates on loans, savings accounts, and investments relies heavily on percentage calculations. For example, calculating simple interest involves multiplying the principal amount by the interest rate (as a decimal) and the time period.
- Discounts and Sales Tax: Retail stores frequently offer discounts expressed as percentages. Calculating the final price after a discount requires subtracting the percentage discount from the original price. Similarly, calculating sales tax involves adding a percentage of the price to the original cost.
- Investment Returns: Investors use percentage changes to track the performance of their investments. A positive percentage change indicates growth, while a negative percentage change represents a loss. Understanding compound interest, which involves earning interest on both the principal and accumulated interest, requires proficiency in percentage calculations.
2. Data Analysis and Statistics:
- Statistical Measures: Many statistical measures, such as percentages, proportions, and rates, are expressed as percentages. For example, calculating the percentage of students who passed an exam or the percentage change in unemployment rates involves percentage calculations.
- Data Representation: Percentages are frequently used to represent data in charts, graphs, and tables. For instance, pie charts visually display the proportion of different categories as percentages of a whole.
- Probability: Percentage calculations are integral to understanding and applying probability concepts. For example, expressing the probability of an event occurring as a percentage helps to understand the likelihood of that event happening.
3. Everyday Life:
- Tips and Gratuities: Calculating tips in restaurants or gratuities for services often involves determining a percentage of the total bill.
- Ingredient Ratios: Recipes frequently specify ingredient amounts as percentages of the total mixture. This is particularly useful for scaling recipes up or down.
- Comparisons and Proportions: Percentages allow for easy comparisons between different quantities or values. For example, comparing the percentage of market share held by different companies provides valuable insights into industry dynamics.
Advanced Percentage Calculations: Beyond the Basics
While the simple percentage calculation shown earlier provides a foundation, several more complex scenarios require additional techniques. These include:
-
Calculating percentage increase or decrease: This involves finding the percentage change between two values. The formula is:
[(New Value - Old Value) / Old Value] * 100%. For example, if a stock price increases from $10 to $12, the percentage increase is [(12-10)/10] * 100% = 20%. -
Finding the original value after a percentage increase or decrease: If you know the final value and the percentage change, you can work backward to find the original value. This often involves using algebraic manipulation of the percentage change formula.
-
Calculating compound interest: Compound interest involves earning interest on both the principal and accumulated interest. The formula for compound interest is:
A = P (1 + r/n)^(nt), where A is the final amount, P is the principal amount, r is the annual interest rate, n is the number of times interest is compounded per year, and t is the number of years. -
Solving percentage word problems: Many real-world applications of percentages involve translating word problems into mathematical equations. Careful reading and understanding of the problem's context are crucial for setting up the correct equation.
Conclusion: Mastering Percentage Calculations for Success
Understanding percentage calculations is a fundamental skill with far-reaching implications across diverse fields. From navigating financial decisions and analyzing data to understanding probability and making everyday comparisons, the ability to work with percentages effectively is essential for success in both personal and professional life. By mastering the basic concepts and exploring more advanced techniques, individuals can equip themselves with a powerful tool for solving problems and making informed decisions in a world saturated with numerical data. The seemingly simple question, "200 is what percent of 40?", ultimately serves as a gateway to unlocking a wealth of practical applications and deeper mathematical understanding.
Latest Posts
Latest Posts
-
What Is 80 Percent Of 200
May 14, 2025
-
3 To The Power Of 100
May 14, 2025
-
Density Of Water At 70 Degrees Fahrenheit
May 14, 2025
-
3 5 Cubic Feet To Cubic Inches
May 14, 2025
-
80 Trillion Divided By 8 Billion
May 14, 2025
Related Post
Thank you for visiting our website which covers about 200 Is What Percent Of 40 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.