21 Is What Percent Of 20
Treneri
May 10, 2025 · 4 min read
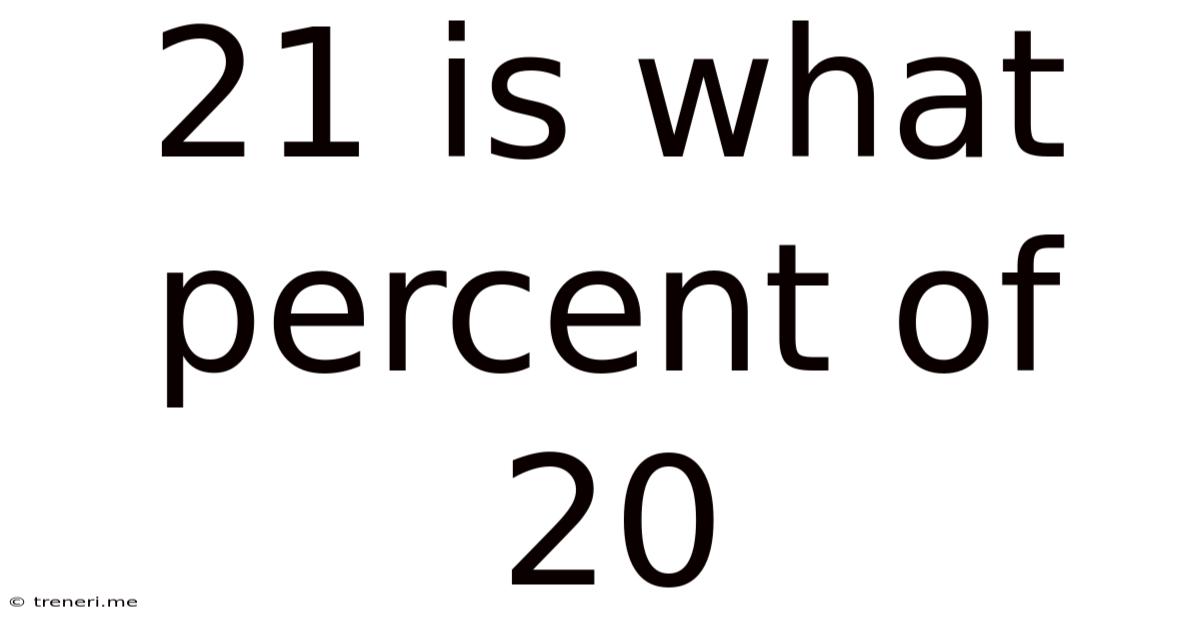
Table of Contents
21 is What Percent of 20? A Deep Dive into Percentage Calculations and Their Applications
The seemingly simple question, "21 is what percent of 20?" opens the door to a fascinating exploration of percentages, their practical applications, and the underlying mathematical principles. While a quick calculation might suffice for a simple answer, a deeper understanding reveals the power and versatility of percentage calculations across numerous fields. This article will not only provide the answer but also delve into the methodology, explore various applications, and offer practical tips for mastering percentage calculations.
Understanding Percentages: The Basics
Before we tackle the core question, let's solidify our understanding of percentages. A percentage is simply a fraction expressed as a number out of 100. The term "percent" itself comes from the Latin "per centum," meaning "out of one hundred." Therefore, 50% means 50 out of 100, or 50/100, which simplifies to 1/2 or 0.5.
This fundamental concept is crucial for understanding and solving percentage problems. Percentages are ubiquitously used to represent proportions, ratios, and changes in various contexts. From calculating discounts in a shopping mall to understanding economic growth rates, percentages are indispensable tools for interpreting data and making informed decisions.
Calculating "21 is What Percent of 20?"
Now, let's address the central question: "21 is what percent of 20?" To solve this, we can employ a simple formula:
(Part / Whole) * 100 = Percentage
In our case:
- Part: 21
- Whole: 20
Substituting these values into the formula, we get:
(21 / 20) * 100 = 105%
Therefore, 21 is 105% of 20. This result highlights an important point: percentages can exceed 100%. This occurs when the "part" is larger than the "whole," indicating a value greater than the reference point.
Beyond the Calculation: Understanding the Implication
The result of 105% is not just a numerical answer; it signifies a significant increase. This outcome could be interpreted in various contexts. For example:
- Sales Growth: If 20 represents last year's sales and 21 represents this year's sales, it indicates a 5% increase.
- Project Overrun: If 20 represents the budgeted amount for a project and 21 represents the actual cost, it signifies a 5% budget overrun.
- Population Increase: If 20 represents the initial population and 21 represents the population after a period, it signifies a 5% population growth.
Understanding the context in which the percentage is calculated is paramount to correctly interpreting and utilizing the result. The numerical answer alone may not fully convey the meaning and implication without considering the relevant context.
Practical Applications of Percentage Calculations
Percentage calculations find widespread application in numerous fields. Here are just a few examples:
- Finance: Calculating interest rates, returns on investments, loan payments, and tax rates.
- Business: Determining profit margins, sales growth, market share, and discounts.
- Science: Expressing concentrations, error margins, and statistical probabilities.
- Everyday Life: Calculating tips, sales tax, discounts, and nutritional values in food.
- Education: Evaluating student performance, calculating grades, and representing statistical data in research.
Mastering percentage calculations is essential for success in various professional and personal endeavors. The ability to quickly and accurately compute percentages provides a significant advantage in making informed decisions and interpreting data effectively.
Advanced Percentage Calculations: More Complex Scenarios
While the basic percentage calculation is straightforward, more complex scenarios require a deeper understanding. These might include:
- Calculating Percentage Increase or Decrease: These calculations involve determining the percentage change between two values. The formula is:
((New Value - Old Value) / Old Value) * 100 - Finding the Original Value: This involves working backward from a percentage to determine the original value.
- Solving Problems Involving Multiple Percentages: This could involve calculating consecutive percentage changes or combining different percentages.
These advanced techniques necessitate a strong grasp of algebraic manipulation and problem-solving skills.
Tips for Mastering Percentage Calculations
- Practice Regularly: Consistent practice is key to mastering any mathematical concept, including percentage calculations.
- Utilize Different Methods: Experiment with different approaches to solving percentage problems to find the method that works best for you.
- Use Visual Aids: Diagrams, charts, and other visual aids can help to visualize percentage relationships and make them easier to understand.
- Check Your Answers: Always double-check your calculations to ensure accuracy.
- Learn to Estimate: Developing the ability to quickly estimate percentages can be helpful in everyday situations.
Conclusion: The Significance of Understanding Percentages
The seemingly simple question, "21 is what percent of 20?" has led us on a journey into the world of percentages – their definition, calculation, applications, and their practical implications across diverse domains. Understanding percentages is not merely an academic exercise; it's a fundamental skill applicable to various aspects of life, from personal finance to professional success. By mastering percentage calculations, we equip ourselves with a powerful tool for interpreting data, making informed decisions, and navigating the complexities of the world around us. The 105% answer is more than just a number; it’s a gateway to a deeper understanding of quantitative reasoning and its crucial role in our daily lives. Continuous learning and practice will solidify this understanding, paving the way for greater confidence and competence in tackling various mathematical challenges.
Latest Posts
Latest Posts
-
What Size Of Wire For 100 Amps
May 11, 2025
-
How Big Is A 7 Inch Pizza
May 11, 2025
-
36 Feet Equals How Many Yards
May 11, 2025
-
How To Find Weight Of A Cylinder
May 11, 2025
-
Lowest Common Multiple Of 5 And 11
May 11, 2025
Related Post
Thank you for visiting our website which covers about 21 Is What Percent Of 20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.