22 5 As A Mixed Number
Treneri
May 13, 2025 · 4 min read
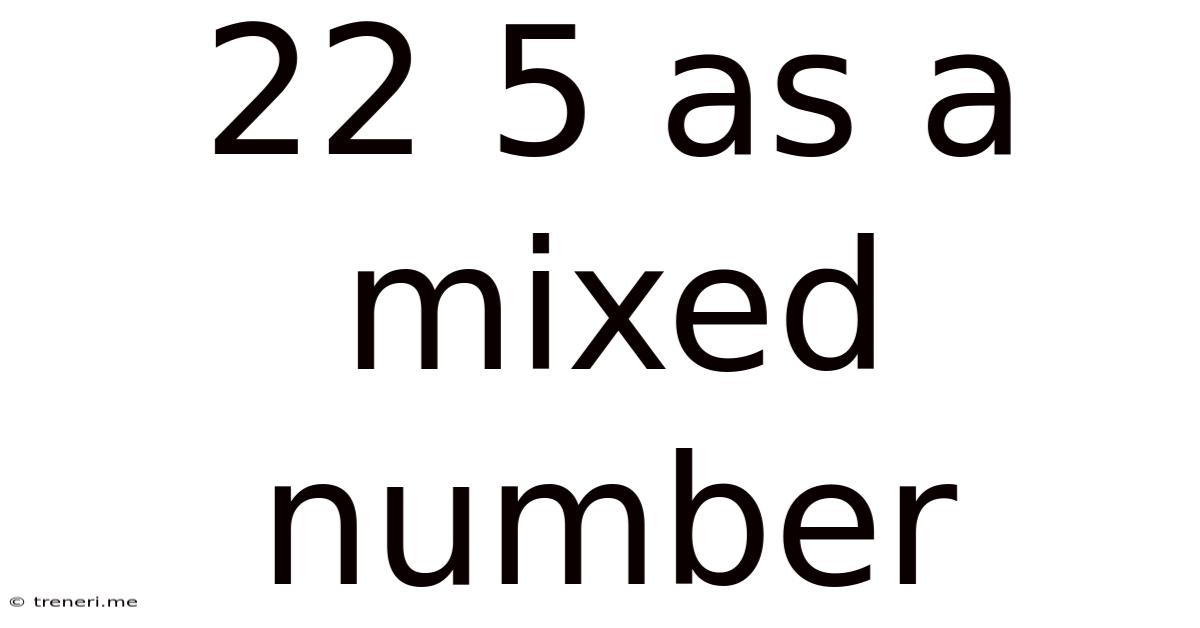
Table of Contents
22/5 as a Mixed Number: A Comprehensive Guide
Understanding fractions and their conversion is fundamental to mathematics. This comprehensive guide delves into the process of converting the improper fraction 22/5 into a mixed number, explaining the concept in detail and providing examples to solidify your understanding. We’ll also explore the broader context of fractions, mixed numbers, and their applications.
What are Improper Fractions and Mixed Numbers?
Before we dive into converting 22/5, let's clarify the terms "improper fraction" and "mixed number."
Improper Fraction: An improper fraction is a fraction where the numerator (the top number) is greater than or equal to the denominator (the bottom number). Examples include 7/4, 11/5, and, of course, 22/5. In essence, it represents a value greater than or equal to one.
Mixed Number: A mixed number combines a whole number and a proper fraction. A proper fraction is one where the numerator is less than the denominator (e.g., 3/4, 1/2, 2/5). Mixed numbers offer a more intuitive way to represent values greater than one. For example, 1 ¾ is a mixed number representing one whole and three-quarters.
Converting 22/5 to a Mixed Number: The Step-by-Step Process
The conversion of 22/5 to a mixed number involves dividing the numerator by the denominator. Here's the breakdown:
-
Divide the numerator by the denominator: Divide 22 by 5. 22 ÷ 5 = 4 with a remainder of 2.
-
The quotient becomes the whole number: The result of the division (4) becomes the whole number part of the mixed number.
-
The remainder becomes the numerator: The remainder (2) becomes the numerator of the fractional part.
-
The denominator remains the same: The denominator (5) stays the same.
Therefore, 22/5 as a mixed number is 4 2/5.
Visual Representation
Imagine you have 22 equally sized pieces of pizza. If each pizza has 5 slices, you can make 4 full pizzas (4 x 5 = 20 slices) and still have 2 slices left over. This leftover 2 slices represents the remaining fraction 2/5. So, you have 4 whole pizzas and 2/5 of a pizza. This visual representation perfectly mirrors the mathematical conversion.
Further Exploration: Working with Fractions and Mixed Numbers
Understanding the conversion from improper fractions to mixed numbers is crucial for various mathematical operations. Here are some key applications and related concepts:
Adding and Subtracting Fractions
When adding or subtracting fractions with different denominators, converting to mixed numbers can simplify the process. Let's consider an example:
Add 22/5 and 7/5. We already know 22/5 = 4 2/5. Then:
4 2/5 + 7/5 = 4 (2/5 + 7/5) = 4 (9/5)
Now, we convert 9/5 to a mixed number (1 4/5):
4 (1 4/5) = 5 4/5
Multiplication and Division of Fractions
While conversion to mixed numbers isn't strictly necessary for multiplication and division of fractions, it can sometimes improve clarity and simplify the calculation, especially when dealing with larger numbers. For example, multiplying 22/5 by 3/4 is easier to conceptualize if you think about multiplying 4 2/5 by 3/4.
Real-World Applications
The concept of mixed numbers is extensively used in various real-world scenarios:
-
Cooking and Baking: Recipes often involve measurements using fractions and mixed numbers (e.g., 2 ½ cups of flour).
-
Construction and Engineering: Precise measurements in construction and engineering frequently necessitate the use of fractions and mixed numbers.
-
Time Measurement: The time 2:30 (two and a half hours) is a mixed number representation (2 ½ hours).
Beyond 22/5: Practicing Fraction Conversion
Mastering fraction conversion requires practice. Here are some additional examples to work through:
- Convert 17/3 to a mixed number.
- Convert 29/6 to a mixed number.
- Convert 35/8 to a mixed number.
Remember the steps: Divide the numerator by the denominator, use the quotient as the whole number, the remainder as the new numerator, and keep the original denominator.
Troubleshooting Common Mistakes
A common mistake is incorrectly calculating the remainder during the division process. Double-check your division work to ensure accuracy. Another common error is forgetting to retain the original denominator in the final mixed number.
Conclusion: Mastering Fractions for Mathematical Proficiency
Understanding the conversion of improper fractions to mixed numbers, as illustrated with the example of 22/5, is a fundamental skill in mathematics. This process empowers you to work more efficiently with fractions, simplifying calculations and enhancing your problem-solving abilities. Regular practice and a clear understanding of the underlying concepts will strengthen your mathematical skills and broaden your capabilities in various quantitative fields. Remember to visualize the process, and always double-check your calculations for accuracy!
Latest Posts
Latest Posts
-
1 3 Cubic Yard Of Sand Weight
May 13, 2025
-
6 Cups Equal How Many Quarts
May 13, 2025
-
1 Lb Peanut Butter Equal Many Cups
May 13, 2025
-
Cuanto Equivale 5 Libras En Kilos
May 13, 2025
-
What Is A 8 9 Grade Percentage
May 13, 2025
Related Post
Thank you for visiting our website which covers about 22 5 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.