22.5 Is What Percent Of 90
Treneri
May 13, 2025 · 4 min read
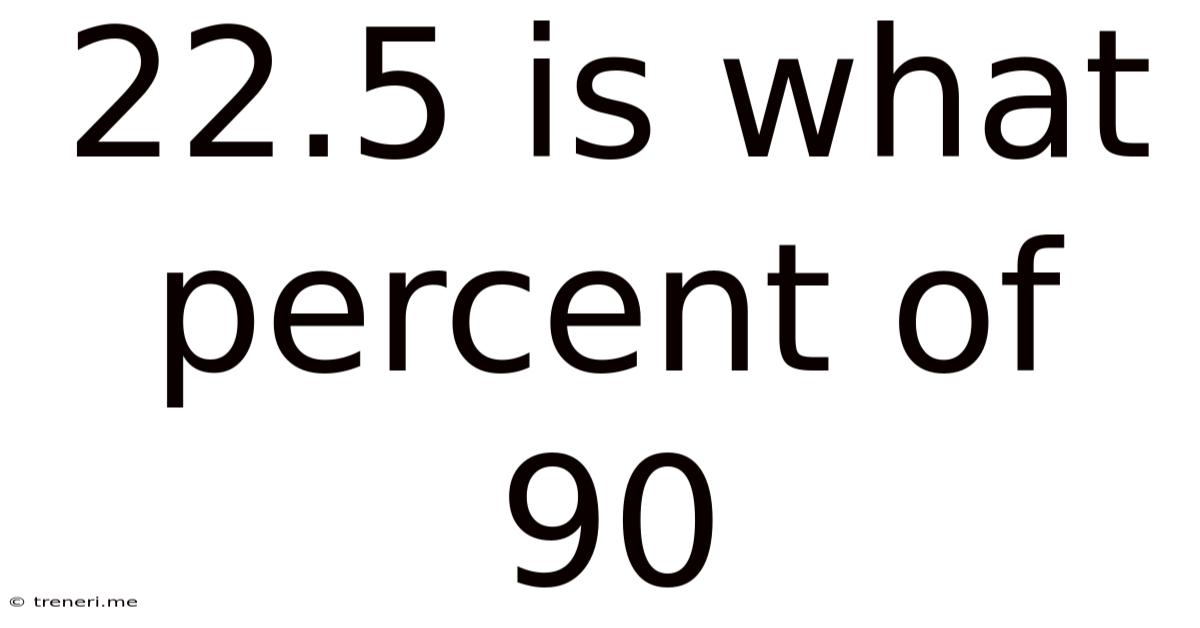
Table of Contents
22.5 is What Percent of 90: A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill in various aspects of life, from calculating discounts and taxes to analyzing data and understanding statistics. This article will delve deep into how to determine what percentage 22.5 represents of 90, explaining the process step-by-step and providing practical applications and extensions to help you master percentage calculations.
Understanding the Fundamentals of Percentages
Before tackling the specific problem of "22.5 is what percent of 90?", let's solidify our understanding of percentages. A percentage is simply a fraction expressed as a part of 100. The symbol "%" denotes percentage. For example, 50% means 50 out of 100, or 50/100, which simplifies to 1/2.
Key Concepts:
- Part: This represents the smaller quantity we're comparing to the whole. In our example, 22.5 is the part.
- Whole: This represents the larger quantity to which the part is being compared. In our example, 90 is the whole.
- Percentage: This represents the portion of the whole that the part constitutes, expressed as a value out of 100. This is what we aim to find.
Calculating the Percentage: Step-by-Step Solution
To determine what percentage 22.5 represents of 90, we'll follow these steps:
Step 1: Set up the equation:
We can represent this problem as a fraction: 22.5 / 90
Step 2: Convert the fraction to a decimal:
Divide the part (22.5) by the whole (90):
22.5 / 90 = 0.25
Step 3: Convert the decimal to a percentage:
Multiply the decimal by 100:
0.25 * 100 = 25
Step 4: Add the percentage symbol:
Therefore, 22.5 is 25% of 90.
Alternative Methods for Calculating Percentages
While the above method is straightforward, there are other ways to approach this type of problem:
Method 1: Using Proportions:
We can set up a proportion:
x/100 = 22.5/90
Cross-multiply:
90x = 2250
Solve for x:
x = 2250 / 90 = 25
Therefore, x = 25%, confirming our previous result.
Method 2: Using the Percentage Formula:
The general formula for calculating percentages is:
(Part / Whole) * 100 = Percentage
Substituting our values:
(22.5 / 90) * 100 = 25%
Real-World Applications of Percentage Calculations
Understanding percentage calculations is crucial in numerous real-world scenarios:
- Finance: Calculating interest rates, discounts, taxes, profits, and losses. For example, determining the interest earned on a savings account or the amount of discount on a sale item.
- Sales and Marketing: Analyzing sales data, tracking conversion rates, and measuring the effectiveness of marketing campaigns. Understanding market share and growth percentages.
- Science and Engineering: Expressing experimental results, calculating error margins, and representing data in graphs and charts.
- Everyday Life: Determining tips in restaurants, calculating sales tax, understanding nutritional information on food labels, and comparing prices.
Advanced Percentage Problems and their Solutions
Let's explore some more complex scenarios involving percentages:
Scenario 1: Finding the Whole when given the Part and Percentage:
-
Problem: 30% of a number is 60. What is the number?
-
Solution: Let the number be 'x'. We can set up the equation:
0.30x = 60
x = 60 / 0.30 = 200
Therefore, the number is 200.
Scenario 2: Finding the Part when given the Whole and Percentage:
-
Problem: What is 15% of 800?
-
Solution: We can calculate this directly:
0.15 * 800 = 120
Therefore, 15% of 800 is 120.
Scenario 3: Percentage Increase or Decrease:
-
Problem: A product's price increased from $50 to $60. What is the percentage increase?
-
Solution:
- Find the difference: $60 - $50 = $10
- Divide the difference by the original price: $10 / $50 = 0.2
- Multiply by 100 to get the percentage: 0.2 * 100 = 20%
Therefore, the price increased by 20%.
Tips and Tricks for Mastering Percentage Calculations
- Practice regularly: The more you practice, the more comfortable you'll become with these calculations.
- Use different methods: Experiment with various approaches to find the method that best suits your understanding.
- Understand the concept: Don't just memorize formulas; strive to understand the underlying principles of percentages.
- Check your work: Always double-check your calculations to ensure accuracy.
- Utilize online calculators: While understanding the process is key, online calculators can help verify your answers and provide additional practice.
Conclusion
Understanding how to calculate percentages is a valuable skill applicable across various fields. This article has provided a detailed explanation of how to determine that 22.5 is 25% of 90, along with alternative methods, real-world applications, and advanced scenarios. By mastering these techniques and practicing regularly, you can confidently tackle percentage problems and apply this knowledge to your daily life and professional endeavors. Remember that consistent practice and a solid understanding of the underlying principles are the keys to mastering percentage calculations.
Latest Posts
Latest Posts
-
1 3 9 To The 3rd Power
May 13, 2025
-
60 Days From July 30 2024
May 13, 2025
-
2 Tbsp Olive Oil In Grams
May 13, 2025
-
How To Get Y Intercept From 2 Points
May 13, 2025
-
30 Quarts Equals How Many Gallons
May 13, 2025
Related Post
Thank you for visiting our website which covers about 22.5 Is What Percent Of 90 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.