24 Is What Percent Of 27
Treneri
May 10, 2025 · 5 min read
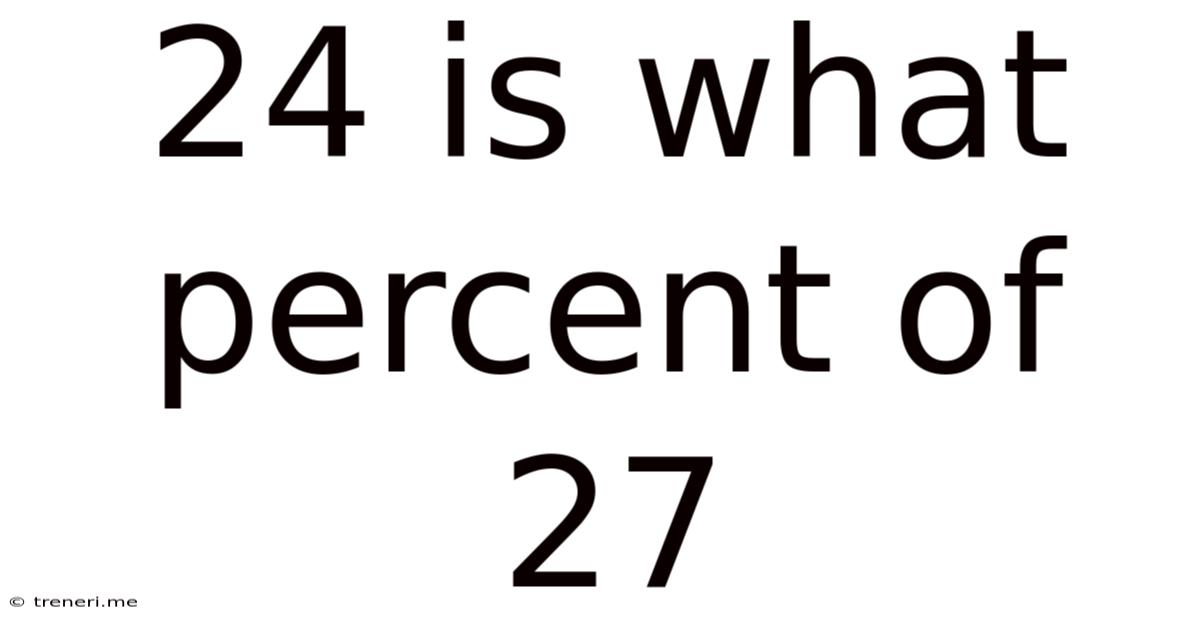
Table of Contents
24 is What Percent of 27? A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill applicable across numerous aspects of life, from calculating discounts and taxes to comprehending statistical data and financial reports. This comprehensive guide will not only answer the question "24 is what percent of 27?" but will also equip you with the knowledge and tools to confidently tackle similar percentage problems. We’ll explore various methods for solving such problems, delving into the underlying concepts and providing practical examples to solidify your understanding.
Understanding Percentages: The Basics
A percentage represents a fraction of 100. It's a way to express a proportion or ratio as a part of a whole, where the whole is always considered 100%. For instance, 50% means 50 out of 100, or one-half. The percentage symbol (%) is used to denote a percentage.
Method 1: Using the Percentage Formula
The most straightforward method to determine what percent 24 is of 27 involves utilizing the fundamental percentage formula:
(Part / Whole) x 100% = Percentage
In this scenario:
- Part: 24 (the number we want to express as a percentage)
- Whole: 27 (the total or reference number)
Substituting these values into the formula:
(24 / 27) x 100% = Percentage
Calculating this:
0.888... x 100% ≈ 88.89%
Therefore, 24 is approximately 88.89% of 27. The slight rounding is due to the recurring decimal in the calculation.
Method 2: Using Proportions
Another approach involves setting up a proportion. We can express the problem as a ratio:
24/27 = x/100
Where 'x' represents the percentage we're trying to find. To solve for 'x', we cross-multiply:
27x = 2400
Then, divide both sides by 27:
x = 2400 / 27
x ≈ 88.89%
This method reinforces the equivalence between fractions, ratios, and percentages.
Method 3: Step-by-Step Breakdown for Clarity
Let's break down the calculation step-by-step for improved understanding, especially for those less familiar with percentage calculations:
-
Divide the part by the whole: 24 / 27 = 0.888...
-
Convert the decimal to a percentage: Multiply the result by 100%: 0.888... x 100% = 88.888...%
-
Round to the desired precision: Rounding to two decimal places gives us 88.89%.
This approach simplifies the process, making it easier to follow each individual step.
Practical Applications of Percentage Calculations
Understanding percentage calculations is crucial in numerous real-world situations. Here are some examples:
-
Discounts: If a $50 item is discounted by 20%, you can calculate the discount amount (20% of $50) and the final price.
-
Taxes: Determining the amount of sales tax or income tax payable involves percentage calculations.
-
Tips: Calculating a restaurant tip based on a percentage of the bill total is a common application.
-
Grades and Scores: Converting raw scores or points obtained in an exam to a percentage score requires these calculations.
-
Financial Analysis: Percentage changes in stock prices, profits, or other financial metrics are essential for investment decisions.
-
Data Interpretation: Analyzing statistical data often involves working with percentages, allowing comparisons and interpretations of various datasets.
-
Sales and Marketing: Tracking conversion rates, click-through rates, and other key performance indicators (KPIs) in marketing frequently involves percentage calculations.
Advanced Percentage Calculations: Finding the Whole or the Part
While our primary focus is on finding the percentage, the same fundamental formula can be rearranged to solve for the whole or the part if those values are unknown:
- Finding the Whole: If you know the percentage and the part, you can find the whole using the formula:
Whole = (Part / Percentage) x 100
- Finding the Part: If you know the percentage and the whole, you can find the part using the formula:
Part = (Percentage / 100) x Whole
These variations of the formula allow you to solve a broader range of percentage problems.
Solving More Complex Percentage Problems
Let's consider some more intricate scenarios to further strengthen your understanding of percentage calculations:
Scenario 1: Successive Percentage Changes
Suppose you have a product initially priced at $100. It's first discounted by 10%, then further discounted by 5%. What's the final price?
-
Step 1: Calculate the first discount: 10% of $100 = $10. The price becomes $90.
-
Step 2: Calculate the second discount: 5% of $90 = $4.50. The final price is $90 - $4.50 = $85.50.
Note that successive percentage changes are not simply additive.
Scenario 2: Percentage Increase
If a company's revenue increases from $50,000 to $60,000, what's the percentage increase?
-
Step 1: Calculate the difference: $60,000 - $50,000 = $10,000.
-
Step 2: Express the difference as a percentage of the original revenue: ($10,000 / $50,000) x 100% = 20%.
The revenue increased by 20%.
Scenario 3: Percentage Points vs. Percentages
It's crucial to understand the distinction between percentage points and percentages. A change from 10% to 15% is a 5 percentage point increase, but a 50% increase relative to the original 10%.
Tips for Mastering Percentage Calculations
-
Practice regularly: The more you practice, the more comfortable you'll become with percentage calculations.
-
Use a calculator: Calculators can significantly speed up the process, especially for more complex problems.
-
Understand the underlying concepts: Don't just memorize formulas; understand why they work.
-
Break down complex problems: Divide complex problems into smaller, manageable steps.
-
Check your work: Always double-check your calculations to ensure accuracy.
Conclusion
Understanding percentages is a versatile skill with wide-ranging applications. By mastering the fundamental formula and its variations, along with practicing different problem-solving approaches, you'll be well-equipped to handle a variety of percentage calculations encountered in daily life and various professional fields. Remember, consistent practice and a firm grasp of the underlying concepts are key to achieving fluency in percentage calculations. The answer to "24 is what percent of 27?" is approximately 88.89%, but more importantly, you've now gained a deeper understanding of how to solve such problems independently.
Latest Posts
Latest Posts
-
3 2 Kilos In Pounds And Ounces
May 10, 2025
-
3 4 Cup Cooked Rice In Grams
May 10, 2025
-
Can A Hamster Live For 5 Years
May 10, 2025
-
What Is Time And A Half For 22 An Hour
May 10, 2025
-
28 Days From July 10 2024
May 10, 2025
Related Post
Thank you for visiting our website which covers about 24 Is What Percent Of 27 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.