25 24 As A Mixed Number
Treneri
May 10, 2025 · 4 min read
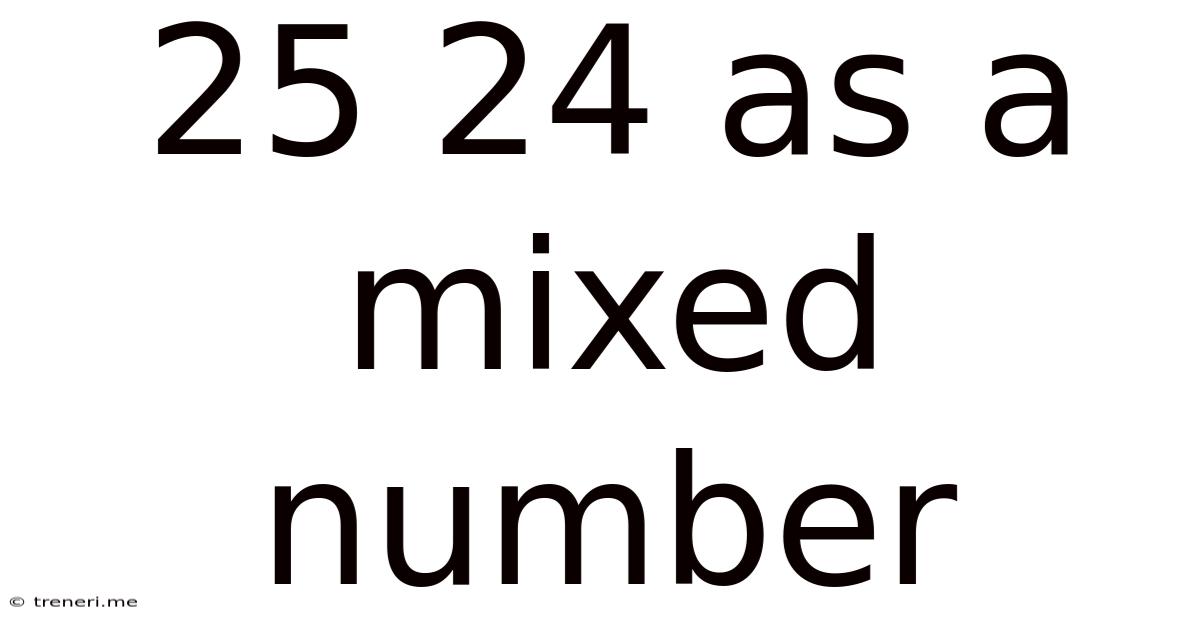
Table of Contents
25/24 as a Mixed Number: A Comprehensive Guide
Understanding fractions and mixed numbers is fundamental to mathematics. This comprehensive guide delves into the process of converting the improper fraction 25/24 into a mixed number, exploring the underlying concepts and providing practical examples to solidify your understanding. We'll also cover related topics like simplifying fractions and solving real-world problems involving mixed numbers.
Understanding Improper Fractions and Mixed Numbers
Before diving into the conversion, let's clarify the terminology:
-
Improper Fraction: An improper fraction is a fraction where the numerator (the top number) is greater than or equal to the denominator (the bottom number). 25/24 is an example of an improper fraction because 25 > 24.
-
Mixed Number: A mixed number combines a whole number and a proper fraction. A proper fraction has a numerator smaller than the denominator. For instance, 1 1/2 is a mixed number.
Converting an improper fraction to a mixed number involves determining how many times the denominator goes into the numerator and expressing the remainder as a fraction.
Converting 25/24 to a Mixed Number: Step-by-Step
The conversion of 25/24 to a mixed number follows these simple steps:
-
Divide the numerator by the denominator: Divide 25 by 24.
25 ÷ 24 = 1 with a remainder of 1.
-
The quotient becomes the whole number: The result of the division (1) becomes the whole number part of the mixed number.
-
The remainder becomes the numerator of the fraction: The remainder (1) becomes the numerator of the fraction part of the mixed number.
-
The denominator remains the same: The denominator of the mixed number remains the same as the denominator of the original improper fraction (24).
Therefore, 25/24 as a mixed number is 1 1/24.
Visualizing the Conversion
Imagine you have 25 slices of pizza, and each pizza has 24 slices. You can make one whole pizza (24 slices) and have 1 slice remaining. This visually represents the mixed number 1 1/24.
Working with Mixed Numbers: Addition and Subtraction
Mixed numbers are frequently used in everyday calculations. Let's explore how to perform basic arithmetic operations with mixed numbers, using examples relevant to our 1 1/24 result.
Addition:
Let's add 1 1/24 to another mixed number, say 2 3/8. To add mixed numbers, we need to find a common denominator for the fractions:
-
Find a common denominator: The least common multiple (LCM) of 24 and 8 is 24.
-
Convert fractions to equivalent fractions with the common denominator:
3/8 becomes 9/24 (multiply both numerator and denominator by 3)
-
Add the whole numbers and the fractions separately:
1 + 2 = 3 1/24 + 9/24 = 10/24
-
Combine the results:
3 + 10/24 = 3 10/24
-
Simplify the fraction (if possible):
10/24 can be simplified to 5/12 by dividing both numerator and denominator by 2.
Therefore, 1 1/24 + 2 3/8 = 3 5/12.
Subtraction:
Subtracting mixed numbers follows a similar process. Let's subtract 1 1/24 from 3 1/6:
-
Find a common denominator: The LCM of 24 and 6 is 24.
-
Convert fractions to equivalent fractions with the common denominator:
1/6 becomes 4/24
-
Subtract the whole numbers and the fractions separately:
3 - 1 = 2 4/24 - 1/24 = 3/24
-
Combine the results:
2 + 3/24 = 2 3/24
-
Simplify the fraction:
3/24 simplifies to 1/8
Therefore, 3 1/6 - 1 1/24 = 2 1/8.
Real-World Applications of Mixed Numbers
Mixed numbers are prevalent in various real-world situations:
-
Cooking and Baking: Recipes often use mixed numbers for ingredient measurements, like 1 1/2 cups of flour or 2 1/4 teaspoons of baking powder.
-
Construction and Engineering: Measurements in construction and engineering frequently involve mixed numbers, such as 2 3/4 inches or 5 1/2 feet.
-
Time: Time is often expressed using mixed numbers, for example, 1 hour and 15 minutes (1 1/4 hours).
-
Finance: Calculating interest or dividing profits might involve working with mixed numbers.
Further Exploration: Simplifying Fractions
Simplifying fractions, also known as reducing fractions to their lowest terms, is crucial for working with mixed numbers efficiently. It involves finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by the GCD.
For example, in the addition problem above, we simplified 10/24 to 5/12 by dividing both by their GCD, which is 2.
Conclusion: Mastering Mixed Numbers
Converting improper fractions to mixed numbers is a fundamental skill in mathematics. Understanding this process, combined with the ability to perform basic arithmetic operations with mixed numbers, is essential for various applications in everyday life and academic pursuits. By mastering these concepts and practicing regularly, you'll develop a strong foundation in fractional arithmetic. Remember to always simplify your fractions to their lowest terms for the most efficient and accurate results. This comprehensive guide has equipped you with the tools and understanding to confidently tackle problems involving mixed numbers and improper fractions. Remember to practice consistently to solidify your understanding and improve your speed and accuracy in solving such problems.
Latest Posts
Latest Posts
-
How Much Is 200 G In Ounces
May 11, 2025
-
What Is 5 Percent Of 90
May 11, 2025
-
How Many Days Away Is May 17
May 11, 2025
-
3 1 2 1 1 4
May 11, 2025
-
How Many Days Since April 30 2023
May 11, 2025
Related Post
Thank you for visiting our website which covers about 25 24 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.