25.4 X 10 To The Power Of 4
Treneri
May 09, 2025 · 6 min read
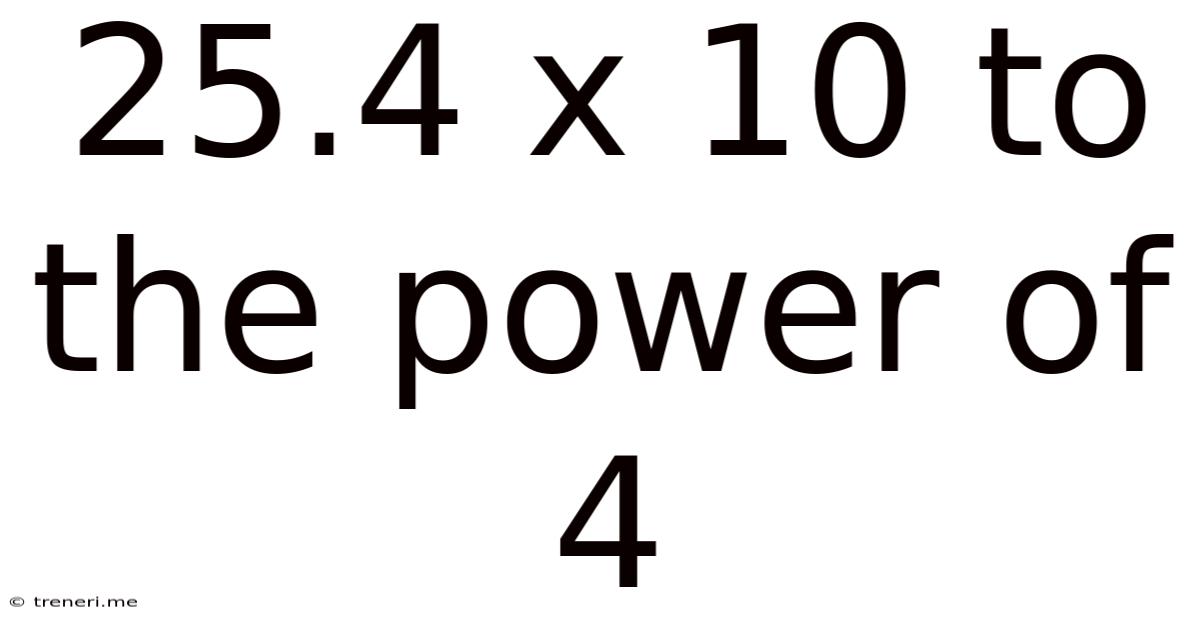
Table of Contents
Decoding 25.4 x 10<sup>4</sup>: Exploring Scientific Notation and its Applications
The seemingly simple expression "25.4 x 10<sup>4</sup>" hides a world of scientific significance. This article delves deep into understanding this notation, exploring its practical applications across various fields, and showcasing how it simplifies complex calculations and data representation. We'll also examine the importance of scientific notation in data analysis, computer science, and even everyday life.
Understanding Scientific Notation
Scientific notation, also known as standard form or exponential notation, is a concise way to represent very large or very small numbers. It's based on powers of 10, making it ideal for handling numbers that would be cumbersome to write in standard decimal form. The general form is:
a x 10<sup>b</sup>
Where:
- 'a' is a number between 1 and 10 (but not including 10). This is often called the coefficient or mantissa.
- 'b' is an integer representing the exponent or power of 10. A positive exponent signifies a large number, while a negative exponent signifies a small number.
In our case, 25.4 x 10<sup>4</sup>, 'a' is 25.4 and 'b' is 4.
Converting 25.4 x 10<sup>4</sup> to Standard Form
To convert this scientific notation to standard decimal form, we simply multiply 25.4 by 10<sup>4</sup>. This means moving the decimal point four places to the right:
25.4 x 10<sup>4</sup> = 254000
Therefore, 25.4 x 10<sup>4</sup> is equivalent to 254,000.
Applications of Scientific Notation:
Scientific notation is not just a mathematical quirk; it's a fundamental tool used across numerous disciplines:
1. Physics and Engineering:
Physics and engineering deal with extremely large and small quantities constantly. Imagine trying to express the distance to the sun (approximately 149,600,000,000 meters) or the size of an atom (on the order of 10<sup>-10</sup> meters) without scientific notation. It would be incredibly cumbersome and error-prone. Scientific notation simplifies these representations significantly, allowing for easier calculations and comparisons. For instance, calculations involving gravitational forces, electrical charges, or wave frequencies are significantly simplified using scientific notation. The use of scientific notation ensures accuracy and precision, vital in complex engineering projects and scientific research.
2. Astronomy and Cosmology:
Astronomy and cosmology grapple with astronomical distances and incredibly massive objects. The distances between stars, galaxies, and other celestial bodies are best expressed using scientific notation. Similarly, the mass of stars and black holes is often orders of magnitude greater than anything we encounter on Earth. Using scientific notation streamlines calculations related to orbital mechanics, stellar evolution, and cosmological models. Without it, the sheer scale of these phenomena would be incredibly difficult to manage and analyze.
3. Chemistry and Biology:
In chemistry, we frequently encounter Avogadro's number (approximately 6.022 x 10<sup>23</sup>), representing the number of atoms or molecules in one mole of a substance. This number is far too large to express comfortably in standard form. Scientific notation becomes essential for calculations involving molar mass, stoichiometry, and reaction rates. In biology, we deal with extremely small quantities, such as the size of viruses or bacteria, which are conveniently expressed using negative exponents in scientific notation. Understanding these microscopic scales is critical for numerous biological processes and research.
4. Computer Science:
Computer science also heavily relies on scientific notation. Computers store and process data in binary format, but representing extremely large or small numbers in binary can be inefficient. Scientific notation provides a more compact and efficient way for computers to handle these values, leading to faster computations and reduced memory usage. Furthermore, scientific notation plays a critical role in algorithms and data structures used in large-scale data analysis and machine learning.
5. Finance and Economics:
While less obvious, scientific notation finds its place in finance and economics as well. National budgets, international trade figures, and global financial markets involve numbers that could easily run into trillions or even quadrillions. Expressing these figures in scientific notation allows for a clearer understanding of their scale and facilitates comparative analysis. Furthermore, algorithms in high-frequency trading and financial modeling rely heavily on efficient numerical representation, and scientific notation contributes to this efficiency.
6. Data Analysis and Statistics:
In data analysis and statistics, dealing with vast datasets is common. Scientific notation helps in summarizing and presenting these large quantities of data in a meaningful way. It simplifies the interpretation of summary statistics, such as means, standard deviations, and correlation coefficients, particularly when these values involve extremely large or small numbers. Moreover, statistical software packages often use scientific notation to display results efficiently, preventing output from being overwhelmingly long or unreadable.
Significance of the Exponent in 25.4 x 10<sup>4</sup>
The exponent, 4, in 25.4 x 10<sup>4</sup> indicates the order of magnitude of the number. It signifies that the number is on the order of 10<sup>4</sup>, or ten thousand. This conveys a quick sense of the size of the number without having to process the full decimal representation. This is particularly useful when comparing several numbers expressed in scientific notation. For instance, comparing 25.4 x 10<sup>4</sup> with 3.2 x 10<sup>5</sup> becomes easy because we can directly compare the exponents and get a sense of the relative magnitude. The latter is an order of magnitude larger.
Practical Calculations with Scientific Notation:
Performing calculations with numbers in scientific notation involves some simple rules:
Multiplication: Multiply the coefficients and add the exponents.
Example: (2.5 x 10<sup>3</sup>) x (4 x 10<sup>2</sup>) = (2.5 x 4) x 10<sup>(3+2)</sup> = 10 x 10<sup>5</sup> = 1 x 10<sup>6</sup>
Division: Divide the coefficients and subtract the exponents.
Example: (6 x 10<sup>5</sup>) / (3 x 10<sup>2</sup>) = (6/3) x 10<sup>(5-2)</sup> = 2 x 10<sup>3</sup>
Addition and Subtraction: The exponents must be the same before performing the operation. Adjust the numbers accordingly, then add or subtract the coefficients, retaining the common exponent.
Example: (2.5 x 10<sup>3</sup>) + (4 x 10<sup>2</sup>) = (2.5 x 10<sup>3</sup>) + (0.4 x 10<sup>3</sup>) = 2.9 x 10<sup>3</sup>
Converting to and from Scientific Notation:
Converting a number from standard form to scientific notation involves identifying the coefficient and determining the exponent. The coefficient is a number between 1 and 10, obtained by moving the decimal point. The exponent is the number of places the decimal point was moved. A rightward move indicates a negative exponent; a leftward move indicates a positive exponent.
For example:
- 0.000052 becomes 5.2 x 10<sup>-5</sup> (decimal moved five places to the right)
- 12345000 becomes 1.2345 x 10<sup>7</sup> (decimal moved seven places to the left)
Conclusion:
25.4 x 10<sup>4</sup>, while appearing simple at first glance, exemplifies the power and utility of scientific notation. This concise method of representing numbers streamlines calculations, improves data presentation, and makes it possible to grapple with extremely large or small values across diverse scientific, engineering, and computational domains. Understanding and utilizing scientific notation is a crucial skill for anyone working with quantitative data. Its widespread application ensures clarity, accuracy, and efficiency in various fields, making it a cornerstone of modern science and technology. As we continue to explore and understand the universe around us, from the smallest subatomic particles to the vast expanse of the cosmos, scientific notation will remain an indispensable tool for researchers and scientists alike.
Latest Posts
Latest Posts
-
14000 Steps Burns How Many Calories
May 09, 2025
-
4 1 2 1 1 2
May 09, 2025
-
3 4 Cup Of Milk In Oz
May 09, 2025
-
How Many Days Is 41 Hours
May 09, 2025
-
How Many Seconds Are There In 10 Mins
May 09, 2025
Related Post
Thank you for visiting our website which covers about 25.4 X 10 To The Power Of 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.