25 Out Of 120 As A Percentage
Treneri
May 15, 2025 · 5 min read
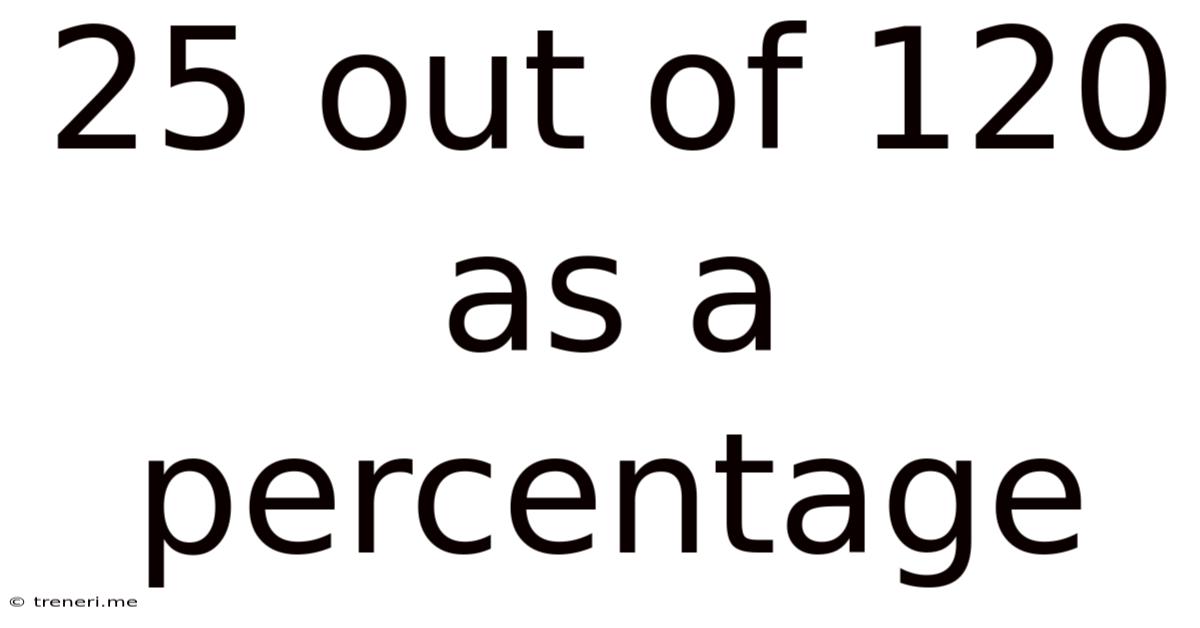
Table of Contents
25 out of 120 as a Percentage: A Comprehensive Guide
Calculating percentages is a fundamental skill with widespread applications in various aspects of life, from academic assessments to financial transactions and everyday decision-making. Understanding how to express a portion of a whole as a percentage is crucial for interpreting data, comparing values, and making informed choices. This article delves into the specific calculation of 25 out of 120 as a percentage, providing a detailed explanation, practical examples, and exploring the broader context of percentage calculations.
Understanding Percentages
A percentage is a fraction or ratio expressed as a number out of 100. The term "percent" literally means "out of one hundred." The symbol % is used to denote percentages. For instance, 50% represents 50 out of 100, or one-half. Percentages provide a standardized way to compare proportions, regardless of the initial values involved. They make it easier to understand and interpret data at a glance.
Calculating 25 out of 120 as a Percentage
To determine the percentage that 25 represents of 120, we need to follow a straightforward calculation:
-
Set up the Fraction: Express the given values as a fraction: 25/120. This fraction represents the portion (25) relative to the whole (120).
-
Convert the Fraction to a Decimal: Divide the numerator (25) by the denominator (120): 25 ÷ 120 = 0.208333...
-
Convert the Decimal to a Percentage: Multiply the decimal by 100: 0.208333... × 100 = 20.8333...%
-
Round the Percentage (if necessary): Depending on the required level of precision, round the percentage to a suitable number of decimal places. Commonly, percentages are rounded to one or two decimal places. In this case, rounding to two decimal places gives us 20.83%.
Therefore, 25 out of 120 is 20.83%.
Practical Applications: Real-World Examples
The calculation of percentages finds application in diverse scenarios:
1. Academic Performance:
Imagine a student scoring 25 marks out of a total of 120 marks in a test. Their percentage score is 20.83%, providing a clear indication of their performance relative to the maximum possible score. This allows for easy comparison with other students and helps assess overall class performance.
2. Financial Calculations:
Consider a scenario where a business made a profit of $25,000 on a total investment of $120,000. The return on investment (ROI) can be expressed as a percentage: 20.83%. This percentage helps investors understand the profitability of the investment. Similarly, discounts, interest rates, and tax calculations frequently involve percentage computations.
3. Statistical Analysis:
In statistical analysis, percentages are fundamental for representing proportions within datasets. For instance, if a survey of 120 people reveals that 25 prefer a particular product, the percentage of respondents preferring that product is 20.83%. This percentage provides a concise summary of the survey results.
4. Sales and Marketing:
In the realm of sales and marketing, percentages are indispensable for analyzing sales figures, tracking conversion rates, and assessing the effectiveness of marketing campaigns. A company might track the percentage of leads that convert into sales or the percentage increase in sales year over year.
5. Everyday Life:
Percentages permeate everyday life in various subtle ways. Tips in restaurants are often calculated as percentages of the bill, while sales discounts are usually presented as percentage reductions from the original price. Understanding percentages empowers us to make informed decisions in these everyday situations.
Beyond the Basics: Advanced Percentage Calculations
While the calculation of 25 out of 120 is a relatively simple example, understanding percentage calculations extends to more complex scenarios:
1. Calculating Percentage Increase or Decrease:
Determining the percentage change between two values requires a slightly different approach. The formula for percentage change is:
Percentage Change = [(New Value - Old Value) / Old Value] × 100
For example, if a value increases from 100 to 125, the percentage increase is: [(125 - 100) / 100] × 100 = 25%.
2. Finding the Original Value:
If you know the percentage and the resulting value, you can calculate the original value. For instance, if a sale price is $75 after a 20% discount, the original price can be found using the following formula:
Original Value = Sale Price / (1 - Discount Percentage)
In this case, the original price would be $75 / (1 - 0.20) = $93.75.
3. Working with Multiple Percentages:
When dealing with successive percentages (e.g., applying a discount and then a tax), it's crucial to remember that the percentages are applied sequentially, not additively. Simply adding the percentages will give an incorrect result. Each percentage should be applied to the intermediate result.
Tips and Tricks for Accurate Percentage Calculations:
-
Use a Calculator: For complex calculations or to ensure accuracy, a calculator is a valuable tool. Many calculators have a percentage function that simplifies the process.
-
Check Your Work: Always double-check your calculations to avoid errors. A minor mistake in the initial steps can lead to a significantly inaccurate final result.
-
Understand the Context: Always pay attention to the context of the problem to ensure you are applying the correct formula and interpreting the results correctly.
-
Practice Regularly: The best way to master percentage calculations is through consistent practice. Work through various examples and problems to build your confidence and proficiency.
Conclusion
Understanding how to calculate percentages is an essential life skill. This article has comprehensively covered the calculation of 25 out of 120 as a percentage (20.83%), explored practical applications in various fields, and provided insights into more advanced percentage calculations. By mastering these techniques, you'll be well-equipped to handle percentage-related problems with confidence and accuracy, improving your ability to interpret data, make informed decisions, and succeed in various aspects of your personal and professional life. Remember to practice regularly and utilize available tools like calculators to enhance your accuracy and efficiency. The ability to confidently work with percentages will undoubtedly prove to be a valuable asset in your journey.
Latest Posts
Latest Posts
-
How Much Is 20 Miles Of Gas
May 15, 2025
-
37 8 As A Mixed Number
May 15, 2025
-
What Uv Is Good For Tanning Outside
May 15, 2025
-
1 2 To The Power Of 4 As A Fraction
May 15, 2025
-
How Many Minutes Is 2400 Seconds
May 15, 2025
Related Post
Thank you for visiting our website which covers about 25 Out Of 120 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.