25 Out Of 32 As A Percentage
Treneri
May 13, 2025 · 5 min read
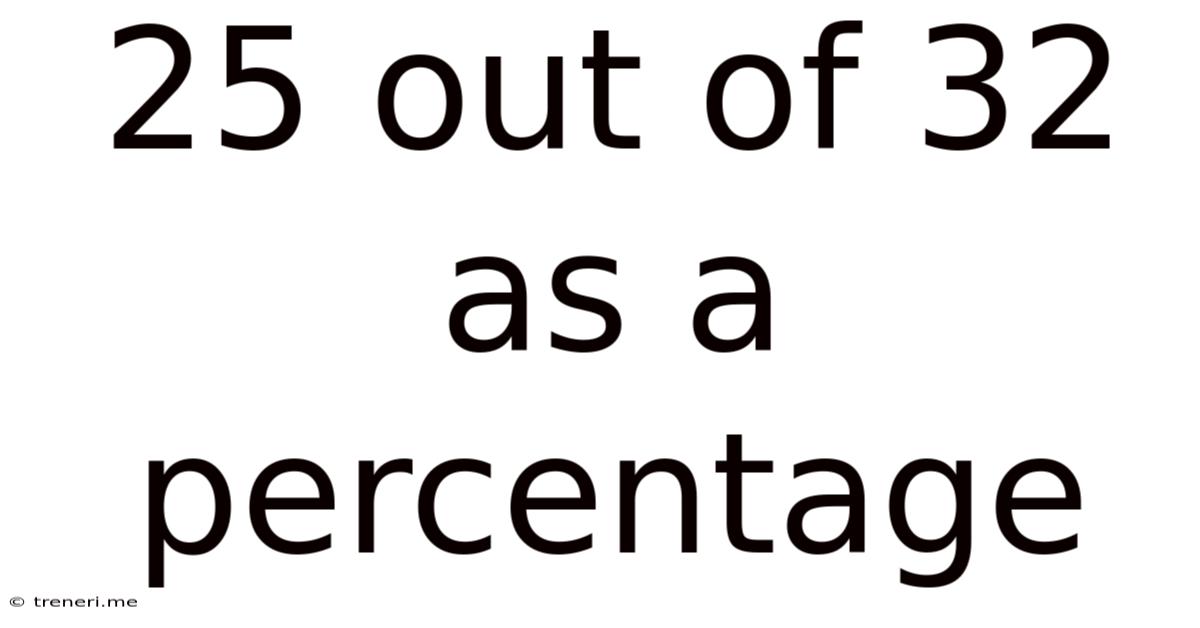
Table of Contents
25 out of 32 as a Percentage: A Comprehensive Guide
Calculating percentages is a fundamental skill applicable across numerous fields, from everyday budgeting to complex scientific research. Understanding how to convert fractions to percentages is crucial for interpreting data, making informed decisions, and communicating results effectively. This article will delve into the specifics of calculating 25 out of 32 as a percentage, providing a step-by-step guide and exploring various related concepts. We'll also discuss the importance of percentage calculations and how to apply this knowledge in different contexts.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "out of one hundred." Therefore, 50% means 50 out of 100, or 50/100, which simplifies to 1/2. This fundamental understanding is key to converting fractions into percentages.
Calculating 25 out of 32 as a Percentage: The Method
To calculate 25 out of 32 as a percentage, we follow these steps:
Step 1: Express the values as a fraction.
25 out of 32 can be written as the fraction 25/32.
Step 2: Convert the fraction to a decimal.
To convert the fraction to a decimal, divide the numerator (25) by the denominator (32):
25 ÷ 32 = 0.78125
Step 3: Convert the decimal to a percentage.
To convert a decimal to a percentage, multiply the decimal by 100 and add the "%" symbol:
0.78125 × 100 = 78.125%
Therefore, 25 out of 32 is equal to 78.125%.
Rounding Percentages
Often, you'll need to round your percentage to a specific number of decimal places. This depends on the context and the level of precision required. For example:
- 78.1%: Rounded to one decimal place. This is suitable for many everyday applications where high accuracy isn't critical.
- 78%: Rounded to the nearest whole number. This is appropriate when a general estimate is sufficient.
- 78.13%: Rounded to two decimal places. This offers more precision than rounding to one decimal place.
The choice of rounding depends on the situation. In scientific contexts, more decimal places might be necessary to maintain accuracy. For simple presentations, rounding to one or two decimal places is often enough.
Applications of Percentage Calculations
Percentage calculations are used extensively in various fields:
1. Finance and Business
- Profit margins: Businesses use percentages to calculate profit margins, comparing profit to revenue.
- Interest rates: Banks and financial institutions use percentages to express interest rates on loans and savings accounts.
- Discounts and sales: Retailers utilize percentages to advertise discounts and sales on products.
- Tax calculations: Governments use percentages to determine tax rates on income, goods, and services.
- Investment returns: Investors use percentages to track the performance of their investments.
2. Education
- Grades and scores: Schools and universities use percentages to represent student grades and test scores.
- Attendance rates: Educational institutions track attendance rates using percentages.
3. Science and Statistics
- Data analysis: Scientists and statisticians use percentages to express and analyze data, represent proportions, and draw conclusions.
- Experimental results: Research often involves calculating percentages to analyze experimental results and determine statistical significance.
4. Everyday Life
- Tips and gratuities: People calculate tips and gratuities as percentages of a bill.
- Shopping discounts: Consumers frequently encounter percentage-based discounts in stores.
- Surveys and polls: Public opinion surveys and polls often represent results as percentages.
Understanding the Context: Why it Matters
The context in which you're calculating 25 out of 32 as a percentage significantly impacts interpretation. For instance:
- 25 out of 32 students passed a test: This means 78.125% of the students passed. This percentage allows for easy comparison with other classes or tests.
- 25 out of 32 attempts were successful: Again, 78.125% success rate. This gives a clear picture of the success ratio.
- 25 out of 32 components are functioning: This indicates 78.125% functionality. This is useful for assessing the reliability of a system.
Understanding the context allows for meaningful interpretation of the calculated percentage, enabling informed decision-making based on the data.
Advanced Percentage Calculations: Related Concepts
While the calculation of 25 out of 32 is straightforward, several related concepts build on this basic understanding:
- Percentage change: This calculation determines the percentage increase or decrease between two values. For example, if a value increases from 20 to 25, the percentage change is calculated as [(25-20)/20] * 100 = 25%.
- Percentage points: This refers to the absolute difference between two percentages. For instance, if interest rates increase from 5% to 10%, the increase is 5 percentage points, not 100%.
- Compound interest: This involves calculating interest not only on the principal amount but also on accumulated interest. This is a more complex calculation but essential in finance.
- Proportions and ratios: Percentage calculations are closely related to proportions and ratios, which express the relative size of different quantities.
Mastering these related concepts expands your ability to analyze and interpret data effectively in various situations.
Practical Tips for Accurate Percentage Calculations
- Use a calculator: While simple calculations can be done manually, a calculator ensures accuracy, especially with more complex percentages or decimal places.
- Check your work: Always double-check your calculations to minimize errors. Simple mistakes can lead to incorrect conclusions.
- Understand the context: Always consider the context of your calculation to ensure you interpret the results accurately.
- Round appropriately: Round percentages to a suitable number of decimal places based on the context and required precision.
Conclusion
Calculating 25 out of 32 as a percentage—resulting in 78.125%—is a fundamental skill with broad applications. Understanding this calculation and the related concepts of percentages, fractions, and decimals allows for effective data analysis and informed decision-making across diverse fields. By mastering these concepts and practicing accurate calculations, you can enhance your problem-solving abilities and confidently navigate numerous situations requiring percentage calculations. Remember to always consider the context and choose appropriate rounding methods for clear and accurate communication of your findings.
Latest Posts
Latest Posts
-
How Big Is 30 Square Meters
May 14, 2025
-
4 Light Years In Earth Years
May 14, 2025
-
How Much Compost Per Square Foot
May 14, 2025
-
4 Ft 7 Inches To Inches
May 14, 2025
-
What Is A 14 Out Of 20 Grade
May 14, 2025
Related Post
Thank you for visiting our website which covers about 25 Out Of 32 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.