26 Divided By 3 With Remainder
Treneri
May 15, 2025 · 5 min read
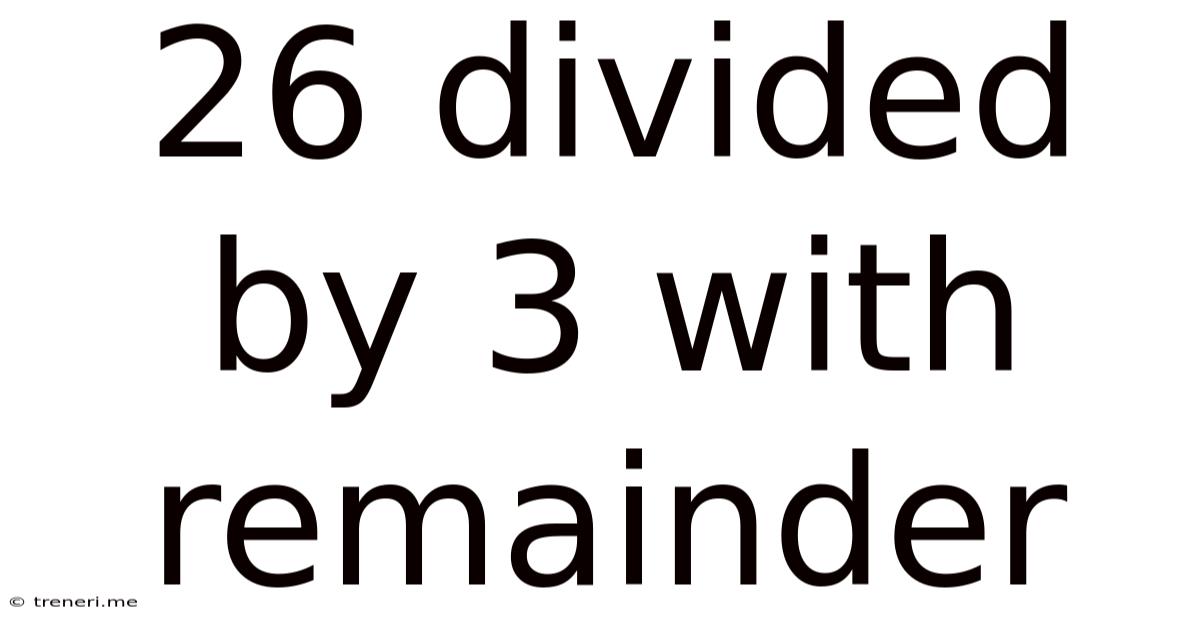
Table of Contents
26 Divided by 3 with Remainder: A Deep Dive into Division and Modular Arithmetic
Division is a fundamental arithmetic operation, and understanding its nuances, including remainders, is crucial for various mathematical applications. This article delves into the seemingly simple problem of dividing 26 by 3, exploring the concept of remainders, their significance, and their applications in different mathematical contexts. We'll also look at how to represent this division using different notations and explore the broader mathematical concepts it relates to.
Understanding Division and Remainders
Division involves splitting a quantity into equal parts. When dividing two integers, we often encounter a situation where the division is not exact, leaving a remaining amount. This remaining amount is called the remainder. In the context of 26 divided by 3, we are essentially asking: "How many times does 3 fit entirely into 26, and what's left over?"
The standard notation for division is:
Dividend ÷ Divisor = Quotient + Remainder/Divisor
Or, using the example of 26 divided by 3:
26 ÷ 3 = 8 R 2
Here:
- 26 is the dividend (the number being divided).
- 3 is the divisor (the number we are dividing by).
- 8 is the quotient (the number of times the divisor goes into the dividend entirely).
- 2 is the remainder (the amount left over after the division).
The remainder is always less than the divisor. If the remainder were equal to or greater than the divisor, it would mean we could have fit the divisor in at least one more time.
Calculating the Remainder
Several methods can be used to calculate the remainder when 26 is divided by 3.
-
Long Division: The traditional method involves performing long division. We find how many times 3 goes into 26 (8 times), multiply 3 by 8 (24), and subtract this from 26, leaving a remainder of 2.
-
Repeated Subtraction: We can repeatedly subtract the divisor (3) from the dividend (26) until we reach a number less than the divisor. This number is the remainder. 26 - 3 = 23; 23 - 3 = 20; 20 - 3 = 17; 17 - 3 = 14; 14 - 3 = 11; 11 - 3 = 8; 8 - 3 = 5; 5 - 3 = 2. The remainder is 2.
-
Modular Arithmetic: This branch of number theory focuses on remainders. The remainder when dividing a by n is written as a mod n. Therefore, 26 mod 3 = 2. This notation elegantly expresses the remainder directly.
Significance of the Remainder
The remainder, seemingly a small detail, holds significant importance in various mathematical and computational contexts:
-
Even and Odd Numbers: Determining whether a number is even or odd involves checking if the remainder is 0 or 1 when divided by 2. Even numbers have a remainder of 0, while odd numbers have a remainder of 1.
-
Cyclic Patterns: Remainders are crucial in identifying cyclic patterns and repeating sequences. For example, the remainders when powers of a number are divided by a particular number often form a cycle.
-
Cryptography: Modular arithmetic and remainders are fundamental to many cryptographic algorithms, ensuring data security and privacy.
-
Hashing: In computer science, hashing functions use modular arithmetic to map large data sets into smaller, fixed-size data structures. The remainder plays a key role in determining the hash value.
-
Computer Science: Remainders are extensively used in algorithms and data structures such as hashing, modular exponentiation, and various other computations.
-
Calendar Calculations: Determining the day of the week for a specific date involves calculating remainders.
-
Number Theory: Remainders form the basis of several crucial concepts in number theory, such as congruence relations and modular arithmetic. The study of remainders provides insights into the properties of numbers and their relationships.
Extending the Concept: Divisibility Rules
Understanding remainders is closely linked to divisibility rules. Divisibility rules offer shortcuts to determine if a number is divisible by another without performing long division. For example:
-
Divisibility by 3: A number is divisible by 3 if the sum of its digits is divisible by 3. In the case of 26, the sum of the digits (2 + 6 = 8) is not divisible by 3, confirming that 26 is not divisible by 3.
-
Divisibility by 9: A number is divisible by 9 if the sum of its digits is divisible by 9.
-
Divisibility by 2: A number is divisible by 2 if its last digit is even (0, 2, 4, 6, or 8).
These divisibility rules are essentially based on understanding the remainder when a number is divided by a specific divisor.
Applications in Real-World Scenarios
The concept of remainders extends beyond theoretical mathematics and finds practical applications in everyday life:
-
Sharing Items: If you have 26 candies to distribute equally among 3 friends, each friend receives 8 candies, and you have 2 candies left over.
-
Scheduling: Suppose you have a task that takes 3 hours to complete, and you have 26 hours available. You can complete the task 8 times within the available time, with 2 hours remaining.
-
Resource Allocation: Distributing resources equally, such as assigning tasks to team members or allocating materials in construction projects often involves considering remainders to ensure efficient allocation.
Conclusion: The Importance of Remainders
The seemingly simple problem of 26 divided by 3, resulting in a quotient of 8 and a remainder of 2, unveils a rich tapestry of mathematical concepts and practical applications. Understanding remainders is not just about performing basic arithmetic but about grasping fundamental principles that underpin various branches of mathematics and computer science. From the elegance of modular arithmetic to the practicality of divisibility rules and real-world applications, the concept of remainders provides a crucial foundation for numerous mathematical and computational processes. The remainder is more than just leftover; it's a key element unlocking deeper understanding in the world of numbers.
Latest Posts
Latest Posts
-
88 83 Is What Percent Of 21
May 15, 2025
-
Cuantas Semanas Tiene Un Ano De 365 Dias
May 15, 2025
-
How Many Ounce In A Kilogram
May 15, 2025
-
How Many Cubic Feet Is 55 Quarts Of Potting Soil
May 15, 2025
-
What Is The Gcf For 18 And 32
May 15, 2025
Related Post
Thank you for visiting our website which covers about 26 Divided By 3 With Remainder . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.