27 16 As A Mixed Number
Treneri
May 13, 2025 · 4 min read
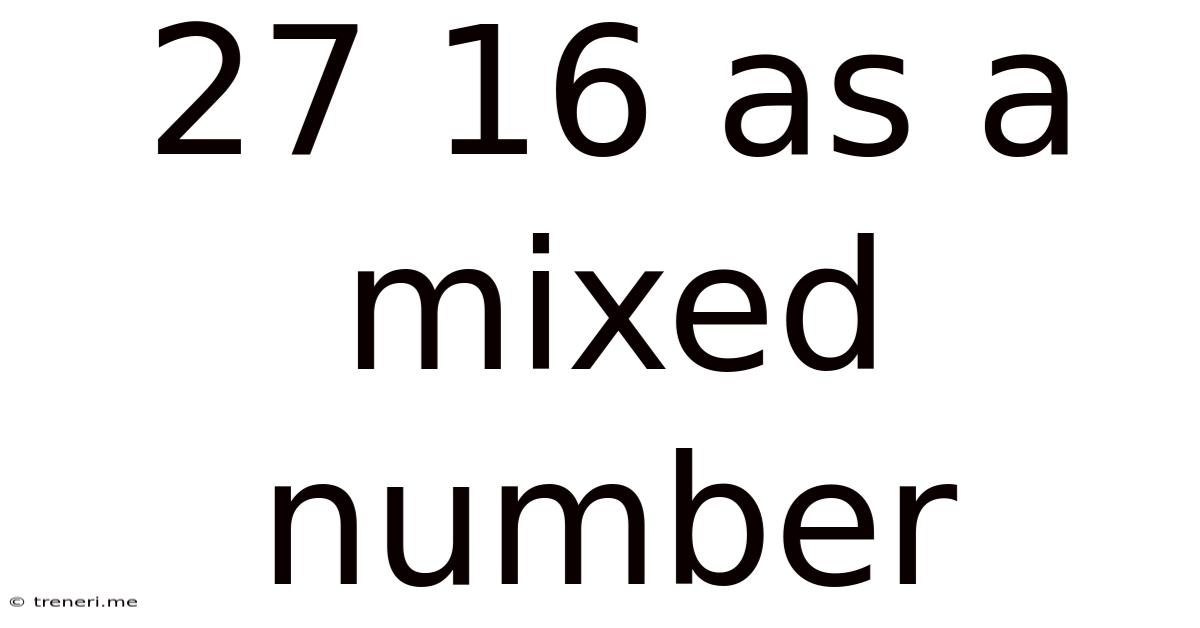
Table of Contents
27/16 as a Mixed Number: A Comprehensive Guide
Converting improper fractions, like 27/16, into mixed numbers is a fundamental skill in mathematics. Understanding this process is crucial for various applications, from baking to engineering. This comprehensive guide will walk you through the conversion of 27/16 to a mixed number, explain the underlying principles, and offer various practical examples. We'll also explore related concepts and provide tips for mastering fraction manipulation.
Understanding Improper Fractions and Mixed Numbers
Before diving into the conversion, let's clarify the terms:
-
Improper Fraction: An improper fraction is a fraction where the numerator (the top number) is greater than or equal to the denominator (the bottom number). 27/16 is an example of an improper fraction because 27 > 16.
-
Mixed Number: A mixed number combines a whole number and a proper fraction. A proper fraction is a fraction where the numerator is less than the denominator. The mixed number equivalent of 27/16 will have a whole number part and a fractional part.
Converting 27/16 to a Mixed Number
The process of converting an improper fraction to a mixed number involves dividing the numerator by the denominator. Let's apply this to 27/16:
-
Divide the numerator by the denominator: 27 ÷ 16 = 1 with a remainder of 11.
-
The whole number part of the mixed number is the quotient: The quotient is 1.
-
The fractional part of the mixed number is the remainder over the original denominator: The remainder is 11, and the original denominator is 16. Therefore, the fractional part is 11/16.
-
Combine the whole number and the fraction: The mixed number is 1 11/16.
Therefore, 27/16 expressed as a mixed number is 1 11/16.
Visualizing the Conversion
Imagine you have 27 slices of pizza, and each pizza has 16 slices. You can form one complete pizza (16 slices) and have 11 slices remaining. This visually represents the mixed number 1 11/16.
Practical Applications of Mixed Numbers
Mixed numbers are incredibly useful in everyday life and various fields:
-
Cooking and Baking: Recipes often use mixed numbers to represent quantities of ingredients, such as 2 1/2 cups of flour or 1 3/4 teaspoons of baking powder.
-
Measurement: Measurements of length, weight, and volume often involve mixed numbers, particularly in imperial units (inches, feet, pounds, etc.).
-
Construction and Engineering: Precise measurements are crucial in these fields, and mixed numbers provide a clear and concise way to represent these measurements.
-
Data Analysis: When dealing with fractional data, representing the results as mixed numbers can provide a more easily understandable format.
Further Exploration of Fractions
Let's delve deeper into related fractional concepts to enhance your understanding:
Simplifying Fractions
While 11/16 is already in its simplest form (the greatest common divisor of 11 and 16 is 1), it's important to understand how to simplify fractions. Simplifying a fraction means reducing it to its lowest terms by dividing both the numerator and the denominator by their greatest common divisor (GCD). For example, if you had 12/18, you'd find the GCD (which is 6), and simplify to 2/3.
Adding and Subtracting Fractions
To add or subtract fractions, they must have a common denominator. If the denominators are different, you'll need to find the least common multiple (LCM) of the denominators and convert the fractions to equivalent fractions with the LCM as the denominator.
For example, to add 1/2 and 1/4, the LCM is 4. We convert 1/2 to 2/4, and then add 2/4 + 1/4 = 3/4.
Multiplying and Dividing Fractions
Multiplying fractions is straightforward: multiply the numerators together and the denominators together. For example, (1/2) * (1/3) = 1/6.
Dividing fractions involves inverting the second fraction (the divisor) and then multiplying. For example, (1/2) ÷ (1/3) = (1/2) * (3/1) = 3/2 = 1 1/2.
Mastering Fraction Manipulation: Tips and Tricks
-
Practice Regularly: Consistent practice is key to mastering fraction manipulation. Work through numerous examples, starting with simpler fractions and gradually increasing the complexity.
-
Use Visual Aids: Visual aids, such as diagrams or physical objects, can help you understand the concepts more clearly.
-
Utilize Online Resources: Many online resources, including educational websites and videos, offer interactive exercises and explanations of fraction concepts.
-
Check Your Work: Always check your answers to ensure accuracy. You can do this by converting your mixed numbers back to improper fractions or by using a calculator to verify your calculations.
Conclusion: The Significance of Understanding Fractions
The ability to convert improper fractions to mixed numbers, and to work confidently with fractions in general, is a cornerstone of mathematical literacy. It's not just an abstract concept; it has practical applications in various aspects of daily life and numerous professions. By mastering these skills, you'll enhance your problem-solving abilities and open doors to a wider range of mathematical challenges. Remember to practice regularly and utilize available resources to build your understanding and confidence in working with fractions. The conversion of 27/16 to 1 11/16 is a small but significant step in this journey. Continue to explore the world of fractions, and you will discover their inherent elegance and practical utility.
Latest Posts
Latest Posts
-
Circumference Of A 20 Foot Diameter Circle
May 14, 2025
-
90 Days After May 22 2024
May 14, 2025
-
Cuanto Es 85 Kg En Libras
May 14, 2025
-
90 Days From September 30 2023
May 14, 2025
-
How Many Days Until June 1 Countdown
May 14, 2025
Related Post
Thank you for visiting our website which covers about 27 16 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.