27 Out Of 36 As A Percentage
Treneri
May 10, 2025 · 4 min read
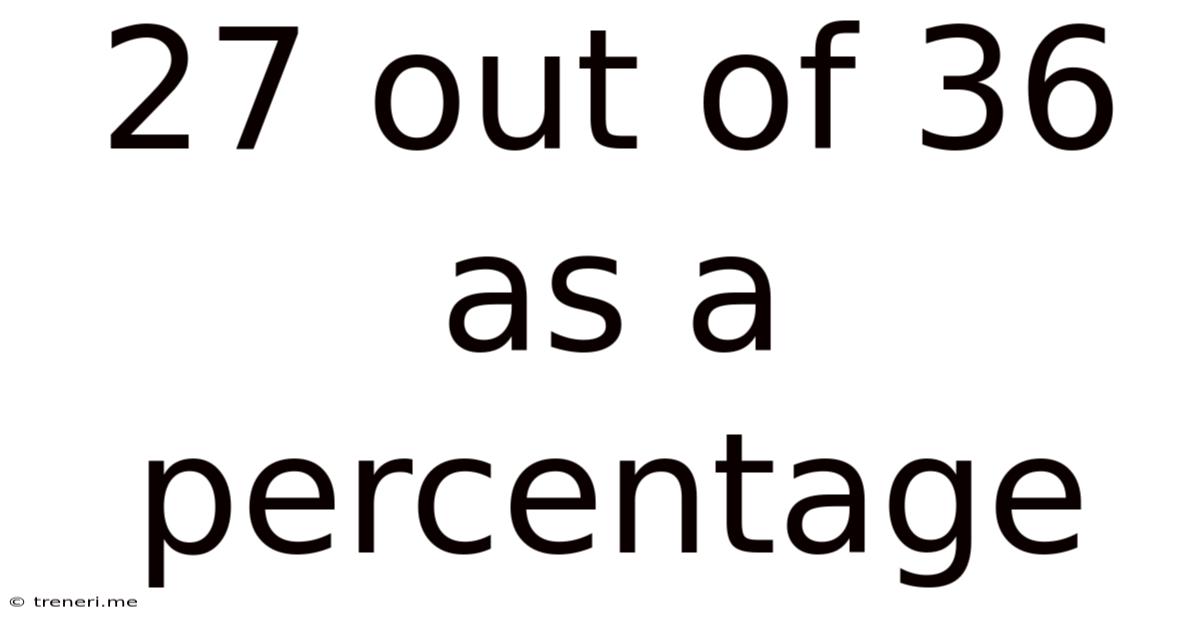
Table of Contents
27 out of 36 as a Percentage: A Comprehensive Guide to Percentage Calculations
Calculating percentages is a fundamental skill with applications across numerous fields, from everyday budgeting and shopping to complex scientific research and financial analysis. Understanding how to express fractions as percentages is crucial for interpreting data, making informed decisions, and communicating information effectively. This comprehensive guide will delve into the calculation of 27 out of 36 as a percentage, and then broaden the scope to provide a robust understanding of percentage calculations in general.
Understanding Percentages:
A percentage is simply a fraction expressed as a number out of 100. The symbol "%" denotes percentage. Essentially, it represents a proportion of a whole. For example, 50% means 50 out of 100, or one half. Understanding this basic concept is key to mastering percentage calculations.
Calculating 27 out of 36 as a Percentage:
The most straightforward method involves converting the fraction 27/36 into a decimal and then multiplying by 100.
Step 1: Convert the Fraction to a Decimal:
To convert a fraction to a decimal, divide the numerator (the top number) by the denominator (the bottom number):
27 ÷ 36 = 0.75
Step 2: Multiply the Decimal by 100:
Multiply the resulting decimal by 100 to express it as a percentage:
0.75 x 100 = 75
Therefore, 27 out of 36 is 75%.
Alternative Method: Simplification and Equivalence
Before resorting to decimal conversion, we can simplify the fraction 27/36. Both 27 and 36 are divisible by 9:
27 ÷ 9 = 3 36 ÷ 9 = 4
This simplifies the fraction to 3/4. We know that 1/4 is 25%, therefore, 3/4 is 3 * 25% = 75%. This method offers a quicker route for certain fractions.
Beyond the Basics: More Complex Percentage Problems
While calculating 27 out of 36 is relatively straightforward, many percentage problems involve more complex scenarios. Let's explore some common variations:
1. Finding the Percentage Increase or Decrease:
These problems typically involve comparing two values to determine the percentage change. The formula is:
[(New Value - Old Value) / Old Value] x 100
For instance, if a price increases from $50 to $60, the percentage increase is:
[(60 - 50) / 50] x 100 = 20%
Similarly, if the price decreases from $60 to $50, the percentage decrease is:
[(50 - 60) / 60] x 100 = -16.67% (Note the negative sign indicating a decrease)
2. Finding a Percentage of a Number:
This involves calculating a portion of a given value. The formula is:
(Percentage / 100) x Number
For example, finding 20% of 150:
(20 / 100) x 150 = 30
3. Finding the Original Value After a Percentage Change:
If you know the final value and the percentage change, you can work backward to find the original value. This requires a slightly different approach. Let's say a price increased by 10% to reach $110. To find the original price:
Let x be the original price. Then, x + 0.1x = 110 1.1x = 110 x = 110 / 1.1 = $100
4. Calculating Percentage Composition:
This is crucial in many contexts, including chemistry and finance. Imagine a mixture containing 27 grams of substance A and 9 grams of substance B. To calculate the percentage composition of substance A:
Total mass = 27 + 9 = 36 grams Percentage of substance A = (27 / 36) x 100 = 75%
Practical Applications of Percentage Calculations:
The ability to calculate percentages is vital in various aspects of life:
- Finance: Calculating interest rates, taxes, discounts, profits, and losses.
- Retail: Determining markups, discounts, and sales tax.
- Science: Expressing experimental results, analyzing data, and comparing measurements.
- Statistics: Representing proportions, analyzing surveys, and conducting statistical analyses.
- Everyday Life: Calculating tips, understanding sales, and budgeting effectively.
Improving your Percentage Calculation Skills:
Mastering percentage calculations involves consistent practice and a solid grasp of the underlying mathematical principles. Here are some helpful tips:
- Practice Regularly: Solve a variety of percentage problems to build confidence and fluency.
- Use Different Methods: Experiment with different approaches to find the most efficient method for each problem.
- Check Your Work: Always verify your calculations to avoid errors.
- Understand the Concepts: Focus on understanding the underlying principles rather than just memorizing formulas.
- Utilize Online Resources: Numerous online calculators and tutorials can provide additional support and practice.
Conclusion:
Calculating 27 out of 36 as a percentage—which equals 75%—is a simple yet illustrative example of a fundamental mathematical concept with wide-ranging applications. By understanding the various methods for calculating percentages and their diverse applications, you can enhance your problem-solving skills and navigate numerous real-world scenarios with confidence. Remember that consistent practice and a solid grasp of the underlying principles are key to mastering percentage calculations and leveraging their power in diverse fields. From simple everyday tasks to complex professional analyses, the ability to work confidently with percentages is a valuable skill that will serve you well throughout your life.
Latest Posts
Latest Posts
-
What Is The Least Common Multiple Of 4 6 9
May 10, 2025
-
What Is 15 Rounded To The Nearest 10
May 10, 2025
-
How Much Is 6 Cups Of Water In Ounces
May 10, 2025
-
Board Foot To Linear Foot Conversion
May 10, 2025
-
Greatest Common Factor Of 27 45 And 63
May 10, 2025
Related Post
Thank you for visiting our website which covers about 27 Out Of 36 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.