2895 Divided By 229 With Remainder
Treneri
May 10, 2025 · 5 min read
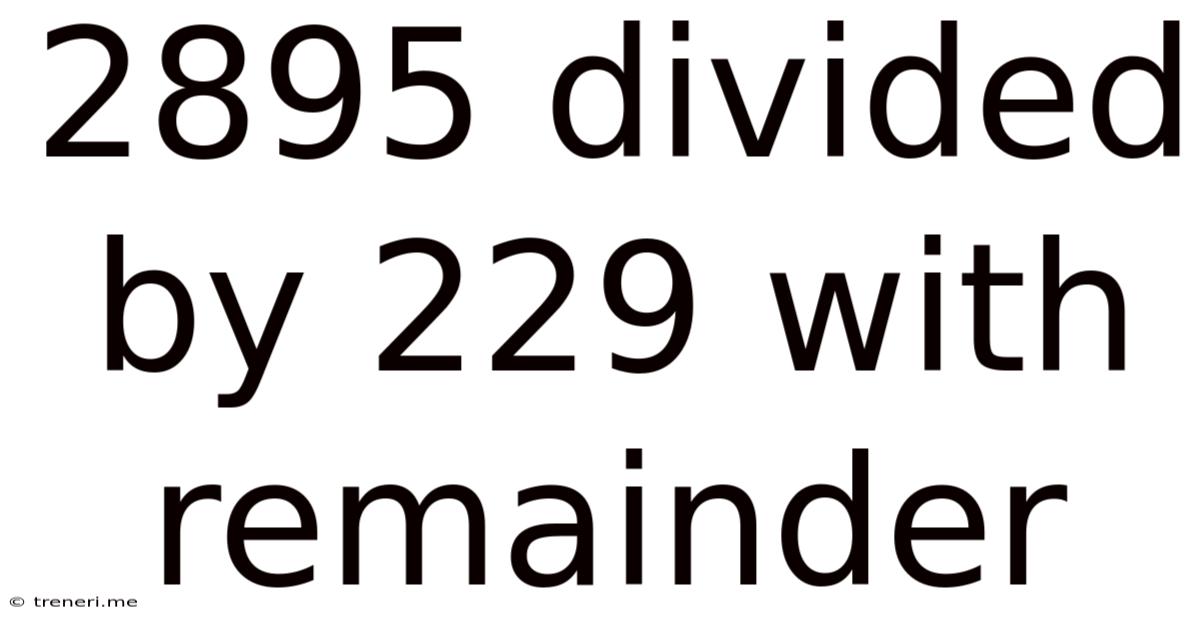
Table of Contents
2895 Divided by 229 with Remainder: A Deep Dive into Division and Its Applications
Dividing 2895 by 229 isn't just a simple arithmetic problem; it's a gateway to understanding fundamental mathematical concepts and their real-world applications. This comprehensive guide will not only solve the problem but also explore the underlying principles, various methods of division, and practical examples where such calculations are crucial.
Understanding the Problem: 2895 ÷ 229
The problem asks us to find the quotient and remainder when 2895 is divided by 229. In simpler terms, we want to determine how many times 229 goes into 2895 completely, and what's left over. This involves the fundamental concept of Euclidean division, which states that for any two integers (a dividend and a divisor), there exist unique integers (a quotient and a remainder) such that:
Dividend = (Divisor × Quotient) + Remainder
Where the remainder is always less than the divisor. In our case:
- Dividend (a): 2895
- Divisor (b): 229
We need to find the quotient (q) and the remainder (r).
Methods for Solving the Problem
Several methods can be used to find the quotient and remainder of 2895 ÷ 229. Let's explore the most common approaches:
1. Long Division
Long division is a classic method that provides a step-by-step breakdown of the division process. It's particularly useful for understanding the underlying mechanics:
-
Set up the problem: Write 2895 inside the long division symbol and 229 outside.
-
Divide: How many times does 229 go into 289? It goes in once (1 x 229 = 229). Write "1" above the 8 in 2895.
-
Multiply: Multiply the quotient (1) by the divisor (229): 1 x 229 = 229.
-
Subtract: Subtract 229 from 289: 289 - 229 = 60.
-
Bring down: Bring down the next digit from the dividend (5), resulting in 605.
-
Repeat: How many times does 229 go into 605? It goes in twice (2 x 229 = 458). Write "2" above the 5 in 2895.
-
Multiply and Subtract: 2 x 229 = 458. Subtract 458 from 605: 605 - 458 = 147.
-
Remainder: The final result is a quotient of 12 and a remainder of 147.
Therefore, 2895 ÷ 229 = 12 with a remainder of 147.
2. Using a Calculator
While less insightful than long division, a calculator provides a quick solution. Most calculators will directly give the quotient and remainder (often represented as a decimal part). However, interpreting the decimal part might require converting it back to a remainder.
For instance, 2895 ÷ 229 ≈ 12.64. The integer part (12) is the quotient. To get the remainder, subtract the quotient from the original number and then multiply by the divisor: (12.64 - 12) * 229 ≈ 147. This confirms our previous result.
Verifying the Result
We can verify our answer using the formula from Euclidean division:
Dividend = (Divisor × Quotient) + Remainder
2895 = (229 × 12) + 147
2895 = 2748 + 147
2895 = 2895
The equation holds true, confirming that our quotient of 12 and remainder of 147 are correct.
Practical Applications of Division with Remainders
Division with remainders isn't just an academic exercise; it has numerous practical applications across various fields:
1. Resource Allocation
Imagine you have 2895 apples to distribute equally among 229 students. The quotient (12) tells you each student receives 12 apples, and the remainder (147) represents the number of apples left over.
2. Scheduling and Time Management
Suppose a task takes 229 minutes to complete, and you have 2895 minutes available. The quotient (12) shows you can complete the task 12 times, with 147 minutes remaining.
3. Manufacturing and Packaging
If you need to package 2895 items into boxes that hold 229 items each, you'll need 12 boxes, and you'll have 147 items left unpackaged.
4. Computer Science and Data Processing
Division with remainders plays a vital role in algorithms for tasks like hashing, modular arithmetic (used in cryptography), and data structures.
5. Geometry and Measurement
Imagine dividing a 2895-meter-long road into sections of 229 meters each. The calculation will reveal the number of sections and the length of the remaining section.
Advanced Concepts Related to Division
Understanding the basic division is a foundation for grasping more advanced mathematical concepts:
-
Modular Arithmetic: The remainder obtained from division is the key element in modular arithmetic, used extensively in cryptography and number theory. The remainder when 2895 is divided by 229 (which is 147) is the result of the modular operation 2895 mod 229.
-
Congruence Relations: Two numbers are congruent modulo n if they have the same remainder when divided by n. For example, 2895 and 147 are congruent modulo 229.
-
Prime Numbers and Divisibility: Understanding remainders helps determine divisibility rules and identify prime numbers. Analysis of remainders is often used in primality testing algorithms.
-
Greatest Common Divisor (GCD): The Euclidean algorithm, a method for finding the GCD of two numbers, relies heavily on repeated division with remainders.
Conclusion
The seemingly simple problem of dividing 2895 by 229 provides a rich learning opportunity. We've explored multiple methods for solving the problem, verified the result, and discussed diverse practical applications. Furthermore, we've touched upon advanced mathematical concepts that build upon the foundational understanding of division and remainders. This illustrates how a single mathematical operation can unlock understanding across various disciplines and pave the way for more complex mathematical explorations. Remember, mastering basic arithmetic operations forms the cornerstone of more sophisticated mathematical endeavors.
Latest Posts
Latest Posts
-
5 Is What Percent Of 20
May 10, 2025
-
How Many Ounces In 3000 Ml
May 10, 2025
-
Cuanto Es 30 Grados Fahrenheit En Celsius
May 10, 2025
-
What Is 6 12 Roof Pitch
May 10, 2025
-
Greater Than Less Than Calculator Decimals
May 10, 2025
Related Post
Thank you for visiting our website which covers about 2895 Divided By 229 With Remainder . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.