3 2/3 X 2 3/4 As A Fraction
Treneri
May 10, 2025 · 5 min read
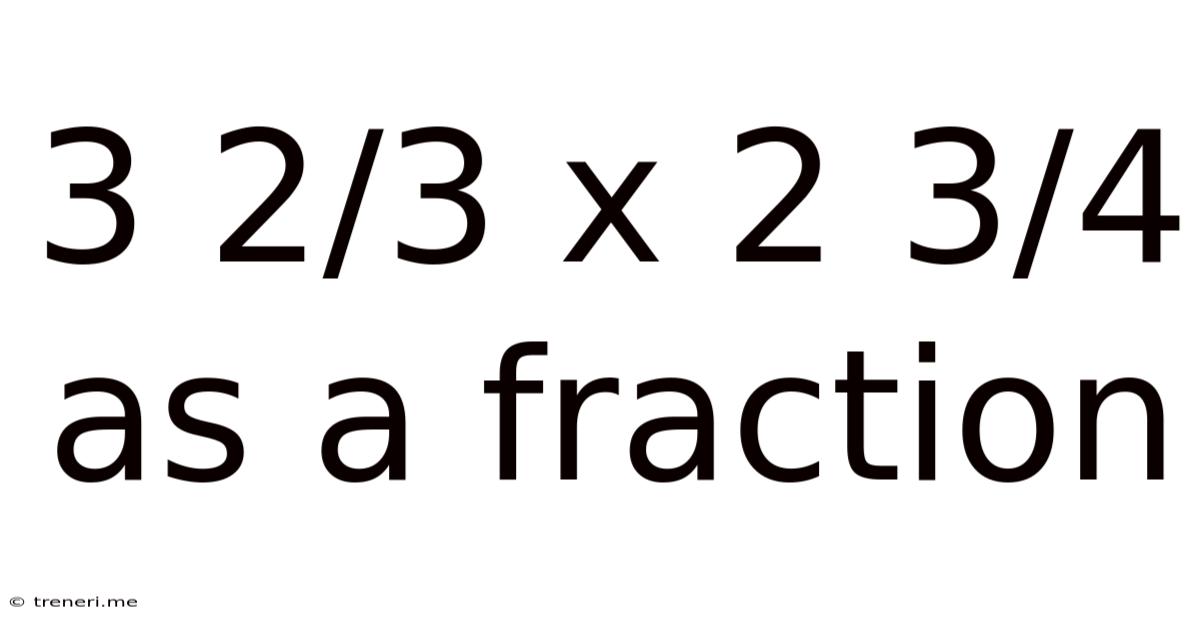
Table of Contents
3 2/3 x 2 3/4 as a Fraction: A Comprehensive Guide
Multiplying mixed numbers might seem daunting, but with a structured approach, it becomes straightforward. This comprehensive guide will walk you through calculating 3 2/3 x 2 3/4 as a fraction, explaining each step in detail and offering valuable insights into working with mixed numbers and fractions. We’ll also explore related concepts and provide practical tips to enhance your understanding.
Understanding Mixed Numbers and Improper Fractions
Before diving into the multiplication, let's solidify our understanding of mixed numbers and improper fractions. A mixed number combines a whole number and a proper fraction (a fraction where the numerator is smaller than the denominator). For example, 3 2/3 represents 3 whole units and 2/3 of another unit.
An improper fraction, conversely, has a numerator larger than or equal to the denominator. It represents a value greater than or equal to one. To convert a mixed number to an improper fraction, we multiply the whole number by the denominator, add the numerator, and keep the same denominator.
Let's convert 3 2/3 to an improper fraction:
(3 x 3) + 2 = 11
The improper fraction is therefore 11/3.
Similarly, let's convert 2 3/4 to an improper fraction:
(2 x 4) + 3 = 11
The improper fraction is 11/4.
Multiplying Improper Fractions: The Core Calculation
Now that we have converted our mixed numbers into improper fractions, we can proceed with the multiplication. Multiplying fractions is relatively simple: we multiply the numerators together and the denominators together.
Our calculation becomes:
11/3 x 11/4 = (11 x 11) / (3 x 4) = 121/12
Converting the Result Back to a Mixed Number
The result, 121/12, is an improper fraction. To make it more understandable and interpretable, we'll convert it back into a mixed number. We do this by performing a division:
121 ÷ 12 = 10 with a remainder of 1
This means that 121/12 is equivalent to 10 whole units and 1/12 of a unit. Therefore, the mixed number representation of 121/12 is 10 1/12.
Step-by-Step Breakdown: 3 2/3 x 2 3/4
Let's recap the entire process step-by-step:
-
Convert Mixed Numbers to Improper Fractions:
- 3 2/3 = 11/3
- 2 3/4 = 11/4
-
Multiply the Improper Fractions:
- 11/3 x 11/4 = 121/12
-
Convert the Resulting Improper Fraction to a Mixed Number:
- 121 ÷ 12 = 10 with a remainder of 1
- Therefore, 121/12 = 10 1/12
Alternative Methods: Exploring Different Approaches
While the method described above is the most straightforward, there are other approaches you could use. These alternative methods can be useful for understanding the underlying principles or for handling more complex calculations.
Method 2: Distributive Property
You can also utilize the distributive property to multiply mixed numbers. This involves expanding the mixed numbers and then performing the multiplication. However, this method can be more complex and prone to errors, especially with larger numbers. Let's illustrate:
3 2/3 x 2 3/4 = (3 + 2/3) x (2 + 3/4)
Expanding this would require using the FOIL method (First, Outer, Inner, Last):
(3 x 2) + (3 x 3/4) + (2/3 x 2) + (2/3 x 3/4)
This calculation leads to: 6 + 9/4 + 4/3 + 6/12
Simplifying this further requires finding a common denominator, which adds extra steps to the calculation. While it demonstrates a different approach, this method is generally less efficient than converting to improper fractions.
Practical Applications and Real-World Examples
Understanding how to multiply mixed numbers is crucial in various real-world scenarios. Consider these examples:
-
Baking: A recipe calls for 2 1/2 cups of flour and you need to double the recipe. Multiplying 2 1/2 by 2 helps you determine the total flour needed.
-
Construction: Calculating the area of a rectangular room with dimensions of 3 1/2 meters by 4 3/4 meters requires multiplying mixed numbers.
-
Sewing: Determining the amount of fabric required for a project often involves calculations with mixed numbers.
-
Finance: Calculating compound interest or determining the total cost after adding sales tax can involve multiplying mixed numbers.
Troubleshooting Common Mistakes and Tips for Success
When working with fractions and mixed numbers, several common mistakes can occur. Here are some tips to avoid errors:
-
Double-check your conversions: Ensure accurate conversion from mixed numbers to improper fractions and vice-versa.
-
Simplify fractions: Always simplify your fractions to their lowest terms.
-
Use a common denominator when adding or subtracting: This is essential for accurate results when adding or subtracting fractions.
-
Practice regularly: The more you practice, the more comfortable and confident you'll become with these calculations.
Expanding Your Knowledge: Further Exploration
This guide provides a comprehensive understanding of multiplying mixed numbers. To deepen your understanding, you might want to explore these additional topics:
-
Working with more complex mixed numbers: Practice with larger mixed numbers and more complex fractions.
-
Dividing mixed numbers: Learn how to divide mixed numbers using similar conversion techniques.
-
Operations with decimals and fractions: Integrate your understanding of mixed numbers with decimal calculations.
-
Applying these techniques in word problems: Practice solving real-world problems that involve multiplying mixed numbers.
By mastering the techniques presented in this guide and consistently practicing, you'll confidently tackle any problem involving the multiplication of mixed numbers, such as 3 2/3 x 2 3/4, and many other similar mathematical challenges. Remember, consistent practice and a clear understanding of the underlying principles are key to success in mastering fractions and mixed number operations.
Latest Posts
Latest Posts
-
Best Size Mirror For 48 Inch Vanity
May 10, 2025
-
How Much Is 3 Ml Of Water
May 10, 2025
-
Cuanto Falta Para El 21 De Noviembre
May 10, 2025
-
What Is A 27 Out Of 31
May 10, 2025
-
How Is True Shooting Percentage Calculated
May 10, 2025
Related Post
Thank you for visiting our website which covers about 3 2/3 X 2 3/4 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.