3/2 Divided By 9/4 As A Fraction
Treneri
May 11, 2025 · 4 min read
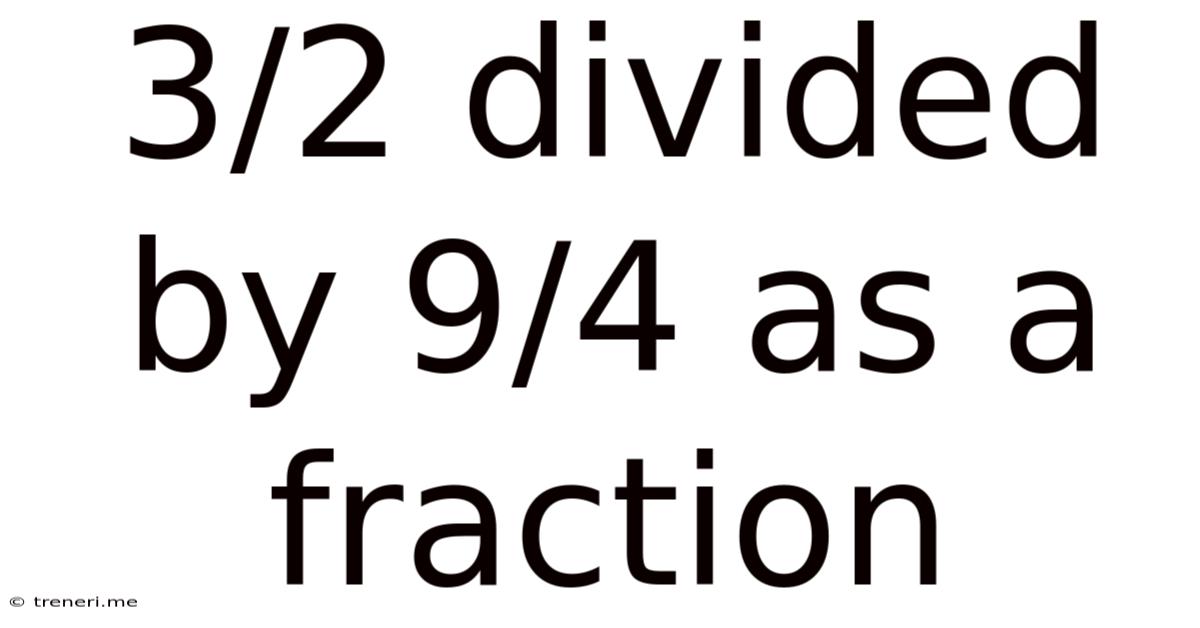
Table of Contents
3/2 Divided by 9/4 as a Fraction: A Comprehensive Guide
Dividing fractions can seem daunting, but with a clear understanding of the process, it becomes straightforward. This article will delve into the division of 3/2 by 9/4, explaining the steps involved, the underlying principles, and providing you with a solid foundation for tackling similar problems. We'll also explore related concepts and offer practical tips to enhance your fractional arithmetic skills.
Understanding Fraction Division
Before diving into the specific problem of 3/2 ÷ 9/4, let's establish a fundamental understanding of fraction division. The core concept revolves around the idea of reciprocals. The reciprocal of a fraction is simply the fraction flipped upside down. For example, the reciprocal of 2/3 is 3/2.
Dividing by a fraction is equivalent to multiplying by its reciprocal. This is the crucial step that transforms a potentially complex division problem into a simpler multiplication problem.
The Formula:
The general formula for dividing fractions is:
(a/b) ÷ (c/d) = (a/b) x (d/c)
Where 'a', 'b', 'c', and 'd' represent numbers, and 'b' and 'c' are not zero (division by zero is undefined).
Solving 3/2 Divided by 9/4
Now, let's apply this formula to our specific problem: 3/2 ÷ 9/4.
Step 1: Identify the Reciprocals
First, we need to find the reciprocal of the second fraction (the divisor), which is 9/4. The reciprocal of 9/4 is 4/9.
Step 2: Convert the Division to Multiplication
Now, we can rewrite the division problem as a multiplication problem:
3/2 ÷ 9/4 = 3/2 x 4/9
Step 3: Multiply the Numerators and Denominators
Next, we multiply the numerators (the top numbers) together and the denominators (the bottom numbers) together:
(3 x 4) / (2 x 9) = 12/18
Step 4: Simplify the Fraction
Finally, we simplify the resulting fraction by finding the greatest common divisor (GCD) of the numerator and the denominator. The GCD of 12 and 18 is 6. Dividing both the numerator and the denominator by 6 gives us the simplified fraction:
12/18 = (12 ÷ 6) / (18 ÷ 6) = 2/3
Therefore, 3/2 divided by 9/4 is equal to 2/3.
Alternative Methods and Considerations
While the method above is the standard approach, there are other ways to solve this problem. Let's explore a couple of them:
Method 2: Simplifying Before Multiplication
We can simplify the fractions before performing the multiplication. Notice that both the numerator of the first fraction (3) and the denominator of the second fraction (9) share a common factor of 3. Similarly, the denominator of the first fraction (2) and the numerator of the second fraction (4) share a common factor of 2. We can cancel these common factors before multiplying:
(3/2) x (4/9) = (3/3) x (4/2) x (1/9) = 1 x 2/1 x (1/3) = 2/3
This approach reduces the complexity of the multiplication and simplifies the final fraction.
Method 3: Using Decimal Conversion (Less Preferred)
While generally less preferred for maintaining accuracy, you can convert the fractions to decimals and then divide. However, this method might lead to rounding errors, particularly with more complex fractions.
3/2 = 1.5 9/4 = 2.25 1.5 ÷ 2.25 = 0.666... ≈ 2/3
Practical Applications and Real-World Examples
Understanding fraction division is crucial in various fields and everyday situations. Here are some examples:
-
Baking: If a recipe calls for 3/2 cups of flour and you want to make 9/4 of the recipe, you'll need to calculate (3/2) ÷ (9/4) * (3/2) cups of flour, which simplifies to 1.5 cups of flour.
-
Sewing: If you have 3/2 yards of fabric and each item requires 9/4 yards of fabric, how many items can you make? The answer is found by dividing (3/2) by (9/4), resulting in 2/3 of an item.
-
Construction: Calculating the amount of materials needed for a project often involves fractional arithmetic.
-
Engineering: Many engineering calculations rely heavily on fraction division.
-
Finance: Determining proportional shares or calculating interest often requires working with fractions.
Expanding Your Knowledge: Further Exploration
To further solidify your understanding of fraction division and related concepts, consider exploring these topics:
- Mixed numbers: Learn how to convert mixed numbers (like 1 ½) into improper fractions before dividing.
- Complex fractions: Understand how to simplify fractions where the numerator or denominator (or both) contain fractions themselves.
- Ratio and proportion: These concepts are closely related to fractions and are essential for solving various problems in different contexts.
- Decimal fractions: Master the conversion between fractions and decimals, and learn how to perform operations with both.
Conclusion: Mastering Fraction Division
Mastering fraction division is a fundamental skill with wide-ranging applications. By understanding the concept of reciprocals, applying the correct formula, and practicing regularly, you can confidently tackle fraction division problems. Remember to always simplify your answer to its lowest terms for the most accurate and efficient solution. The methods outlined in this article, combined with further exploration of related topics, will equip you with the tools to confidently handle any fractional division challenge. Keep practicing, and you'll find that what initially seemed daunting will become second nature.
Latest Posts
Latest Posts
-
Kernels In A Bushel Of Corn
May 12, 2025
-
285 Rounded To The Nearest Hundred
May 12, 2025
-
Cuanto Falta Para El 5 De Febrero
May 12, 2025
-
How Much Is 130 Minutes In Hours
May 12, 2025
-
Como Sacar La Raiz Cuadrada De 8
May 12, 2025
Related Post
Thank you for visiting our website which covers about 3/2 Divided By 9/4 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.