3/2 Divided By 9 As A Fraction
Treneri
May 12, 2025 · 5 min read
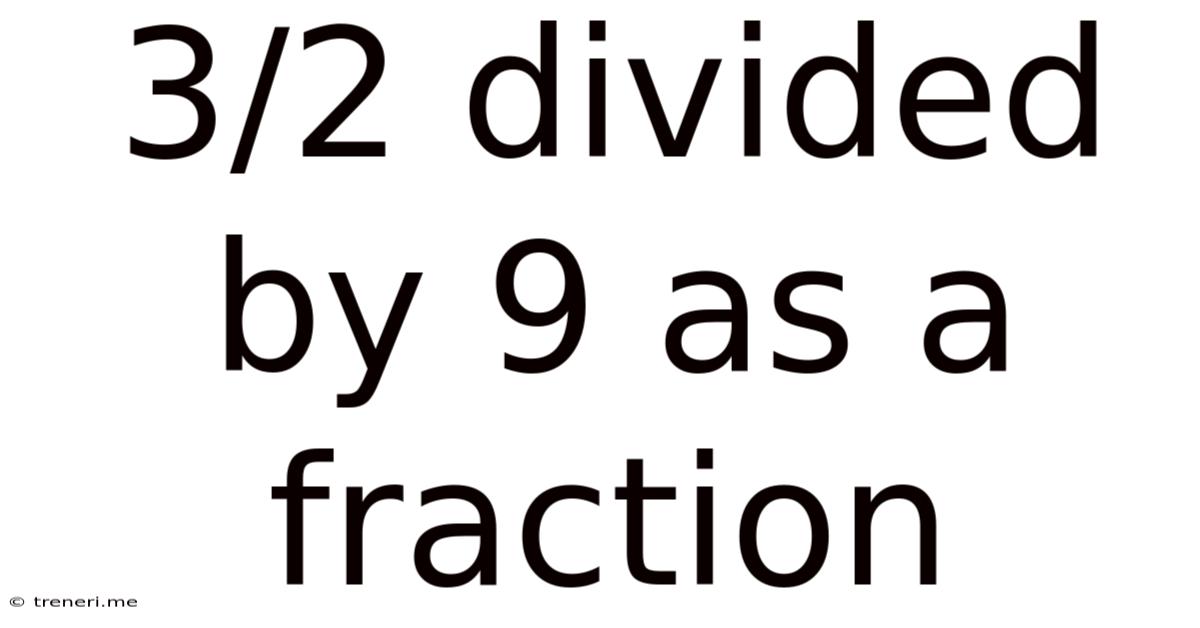
Table of Contents
3/2 Divided by 9: A Comprehensive Guide to Fraction Division
Dividing fractions can seem daunting, but with a clear understanding of the process, it becomes straightforward. This article will delve into the detailed solution of 3/2 divided by 9, explaining the underlying principles and offering practical tips for tackling similar problems. We'll explore various methods, ensuring you gain a comprehensive grasp of fraction division and build confidence in your mathematical abilities.
Understanding Fraction Division
Before we tackle the specific problem of 3/2 divided by 9, let's establish a solid foundation in fraction division. The core concept involves inverting (reciprocating) the second fraction (the divisor) and then multiplying the two fractions. This method elegantly simplifies the division process into a multiplication problem.
The Reciprocal: The Key to Fraction Division
The reciprocal of a fraction is simply the fraction flipped upside down. For instance, the reciprocal of 2/3 is 3/2. The reciprocal of a whole number is that number expressed as a fraction with a denominator of 1. For example, the reciprocal of 9 is 1/9.
The Multiplication Step: Combining Fractions
Once you have the reciprocal of the divisor, the division problem transforms into a multiplication problem. Multiply the numerators (top numbers) together and the denominators (bottom numbers) together. Simplify the resulting fraction to its lowest terms if possible.
Solving 3/2 Divided by 9: A Step-by-Step Approach
Now, let's apply these principles to solve 3/2 divided by 9.
Step 1: Express 9 as a Fraction
First, rewrite the whole number 9 as a fraction: 9/1. This step is crucial for maintaining consistency in our calculations.
Step 2: Find the Reciprocal of the Divisor
The divisor in this problem is 9/1. Its reciprocal is 1/9.
Step 3: Convert Division to Multiplication
The problem now becomes: (3/2) * (1/9)
Step 4: Multiply the Numerators and Denominators
Multiply the numerators: 3 * 1 = 3 Multiply the denominators: 2 * 9 = 18
This gives us the fraction: 3/18
Step 5: Simplify the Fraction
The fraction 3/18 can be simplified. Both the numerator and the denominator are divisible by 3.
3 ÷ 3 = 1 18 ÷ 3 = 6
Therefore, the simplified fraction is 1/6.
Therefore, 3/2 divided by 9 is equal to 1/6.
Alternative Methods for Solving Fraction Division Problems
While the reciprocal method is the most common and widely used, other methods can also be employed to solve fraction division problems. Understanding these alternative methods can enhance your mathematical flexibility and problem-solving skills.
Method 1: Using a Common Denominator
This method involves finding a common denominator for both fractions before performing the division. This approach can be particularly useful for visualizing the division process. However, it's generally less efficient than the reciprocal method, especially for complex fractions.
Let's illustrate this with our example:
- Convert to common denominator: To divide 3/2 by 9, we first need a common denominator. Since 9 can be expressed as 18/2 (9 * 2 = 18), the problem becomes (3/2) ÷ (18/2).
- Divide the numerators: Now, we simply divide the numerators: 3 ÷ 18 = 1/6.
Method 2: Converting to Decimals (Less Precise)
Converting fractions to decimals before performing division is another approach, though it's less precise as it may introduce rounding errors. This method is usually avoided when dealing with fractions for maintaining accuracy. It's best reserved for situations where an approximate answer is sufficient.
In our example:
- Convert to decimals: 3/2 = 1.5 and 9 = 9.0
- Perform division: 1.5 ÷ 9 = 0.16666... (repeating decimal)
- Convert back to fraction (if necessary): This decimal can then be converted back to a fraction, which would be approximately 1/6. However, this approach may lose accuracy compared to directly working with fractions.
Practical Applications and Real-World Examples of Fraction Division
Fraction division isn't just an abstract mathematical concept; it has numerous practical applications in various fields. Understanding how to solve these types of problems is vital for success in many areas.
-
Cooking and Baking: Scaling recipes up or down often involves fraction division. For example, if a recipe calls for 3/2 cups of flour and you want to halve the recipe, you'd need to calculate (3/2) ÷ 2 = 3/4 cups of flour.
-
Construction and Engineering: Calculations involving dimensions, materials, and quantities frequently involve fractions and their division. Precise calculations are crucial for accuracy and safety in these fields.
-
Finance and Budgeting: Dividing resources or allocating funds often requires working with fractions and proportions.
-
Data Analysis and Statistics: Fraction division plays a crucial role in data interpretation and statistical analysis, especially when dealing with proportions and percentages.
Expanding Your Understanding: Further Exploration of Fractions
Mastering fraction division opens doors to more advanced mathematical concepts. Here are some avenues to explore:
-
Complex Fractions: These fractions have fractions within fractions. Understanding fraction division is essential for simplifying and solving these complex expressions.
-
Mixed Numbers: These numbers combine a whole number and a fraction. Learning how to convert between mixed numbers and improper fractions is crucial for handling division problems involving these number types.
-
Algebraic Fractions: These involve variables in the numerator or denominator, demanding a deeper understanding of both algebraic manipulation and fraction operations.
Conclusion: Mastering Fraction Division for Enhanced Problem-Solving Skills
This comprehensive guide has explored the solution to 3/2 divided by 9, explained the underlying principles of fraction division, and showcased alternative methods. By understanding these concepts and practicing regularly, you'll significantly improve your mathematical skills and enhance your ability to solve a wide range of problems involving fractions. Remember, practice is key! The more you work with fractions, the more comfortable and confident you'll become. So, grab a pencil and paper, and continue practicing your fraction division skills!
Latest Posts
Latest Posts
-
How Much Is 9 Ounces In Cups
May 14, 2025
-
What Is The Length Of Segment Xy
May 14, 2025
-
27 Out Of 36 As A Grade
May 14, 2025
-
How Much Is 34 Acres Worth
May 14, 2025
-
How Long Is 25 000 Minutes
May 14, 2025
Related Post
Thank you for visiting our website which covers about 3/2 Divided By 9 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.