3 4 Divided By 1 3 As A Fraction
Treneri
May 12, 2025 · 4 min read
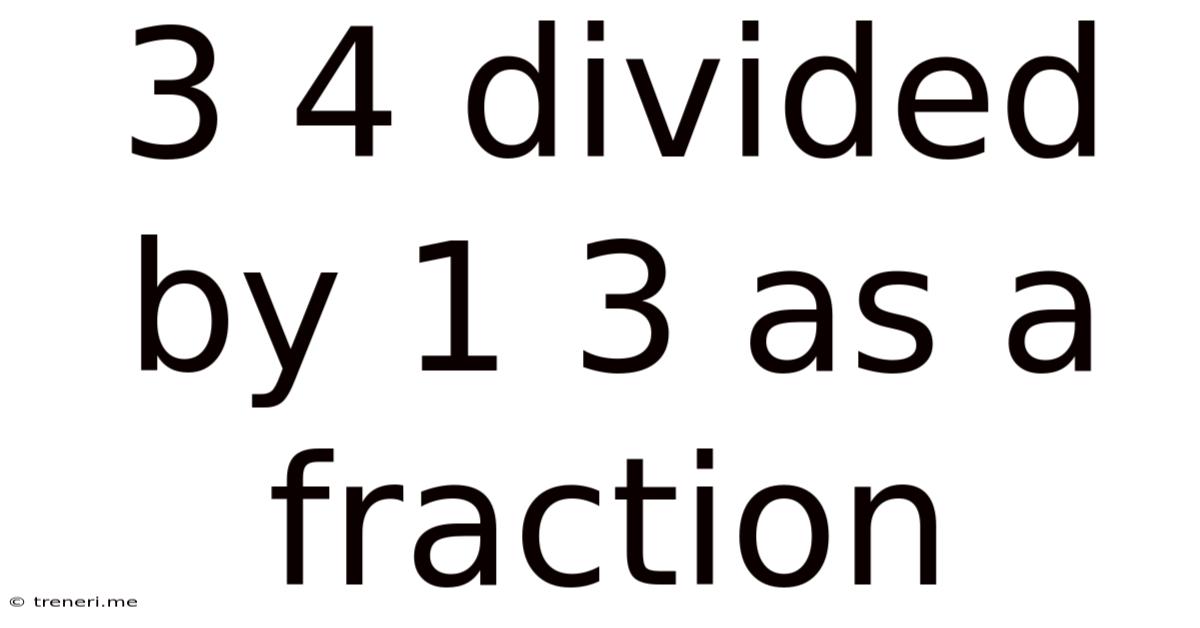
Table of Contents
3 4/13 as a Fraction: A Comprehensive Guide
The seemingly simple question of representing the mixed number 3 4/13 as a fraction might appear straightforward, but understanding the underlying principles and exploring the various methods for solving it can reveal valuable insights into fractional arithmetic. This comprehensive guide dives deep into the process, explaining the concepts, demonstrating multiple approaches, and highlighting potential applications.
Understanding Mixed Numbers and Improper Fractions
Before we tackle the conversion, let's clarify the terminology. A mixed number combines a whole number and a proper fraction (a fraction where the numerator is smaller than the denominator). In our case, 3 4/13 is a mixed number: 3 represents the whole number part, and 4/13 represents the fractional part.
An improper fraction, conversely, has a numerator that is greater than or equal to its denominator. Converting a mixed number to an improper fraction is the core of solving our problem. Improper fractions are valuable because they represent a quantity larger than one whole unit, making them suitable for various calculations.
Method 1: Converting to an Improper Fraction Directly
This is the most common and arguably the most efficient method. It involves multiplying the whole number by the denominator and then adding the numerator. The result becomes the new numerator, while the denominator remains the same.
Steps:
- Multiply the whole number by the denominator: 3 * 13 = 39
- Add the numerator: 39 + 4 = 43
- Keep the denominator the same: 13
Therefore, 3 4/13 as an improper fraction is 43/13.
Method 2: Visual Representation
For a more intuitive understanding, let's visualize the process. Imagine you have three whole units, each divided into 13 equal parts. This represents 3 * 13 = 39 parts. Adding the additional 4/13 gives us a total of 39 + 4 = 43 parts, still out of 13 equal parts per unit. Hence, we again arrive at 43/13.
Method 3: Breaking Down the Mixed Number
We can also break down the mixed number into its component parts and then add them. This method helps solidify the conceptual understanding.
- Separate the whole number and the fraction: 3 + 4/13
- Convert the whole number to a fraction with the same denominator: 3 can be represented as 39/13 (because 39 ÷ 13 = 3).
- Add the fractions: 39/13 + 4/13 = (39 + 4)/13 = 43/13
This method, though slightly more involved, reinforces the idea of common denominators crucial in fraction addition.
Simplifying the Fraction (If Possible)
In this case, 43/13 is already in its simplest form. A fraction is simplified when the greatest common divisor (GCD) of the numerator and denominator is 1. Since 43 is a prime number (only divisible by 1 and itself), and 13 is also a prime number, their GCD is 1. Therefore, no further simplification is possible.
Applications of Improper Fractions
Improper fractions are incredibly useful in various mathematical contexts:
- Division Problems: Improper fractions naturally arise when dividing quantities. For example, if you divide 43 items equally among 13 people, each person gets 43/13 items.
- Complex Fraction Calculations: When working with complex fractions (fractions within fractions), converting to improper fractions often simplifies the calculation.
- Algebraic Expressions: In algebra, improper fractions frequently appear when solving equations or manipulating expressions involving fractions.
- Real-World Scenarios: Numerous real-world situations involve splitting quantities into parts, leading to improper fractions. Imagine sharing 43 pizzas amongst 13 friends – each friend gets 43/13 of a pizza.
Further Exploration: Decimal Representation
While 43/13 is the correct fractional representation, it can also be expressed as a decimal. Performing the division (43 ÷ 13) yields approximately 3.3077. This decimal representation offers a different perspective on the magnitude of the quantity but lacks the precision and clarity of the fraction, particularly in contexts requiring exact values.
Addressing Potential Common Mistakes
A common mistake is incorrectly adding the whole number and numerator and keeping the original denominator. Remember, the whole number must first be converted to a fraction with the same denominator before addition. Always follow the steps outlined above to ensure accuracy.
Conclusion: Mastering Fraction Conversion
Converting a mixed number like 3 4/13 to an improper fraction (43/13) is a fundamental skill in mathematics. Understanding the underlying concepts and mastering the various methods not only helps in solving specific problems but also builds a stronger foundation for more advanced mathematical concepts. The ability to confidently work with fractions is crucial for success in various fields, from everyday calculations to complex scientific and engineering problems. This comprehensive guide provides a clear and thorough explanation of this vital process, enhancing understanding and promoting proficiency in fractional arithmetic. Remember to practice consistently to fully grasp these concepts and develop fluency in handling fractions. By understanding the "why" behind the methods, you build a more robust and lasting comprehension of this core mathematical principle. The practical applications presented offer further context and illustrate the real-world relevance of converting mixed numbers to improper fractions.
Latest Posts
Latest Posts
-
One Teaspoon Of Cough Syrup Has A Volume Of 5
May 14, 2025
-
4 4 5 As An Improper Fraction
May 14, 2025
-
1 3 Minus 1 2 In Fraction Form
May 14, 2025
-
How To Go From Molarity To Grams
May 14, 2025
-
What Is 90 Percent Of 30
May 14, 2025
Related Post
Thank you for visiting our website which covers about 3 4 Divided By 1 3 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.