3/4 X 5 As A Fraction
Treneri
May 10, 2025 · 5 min read
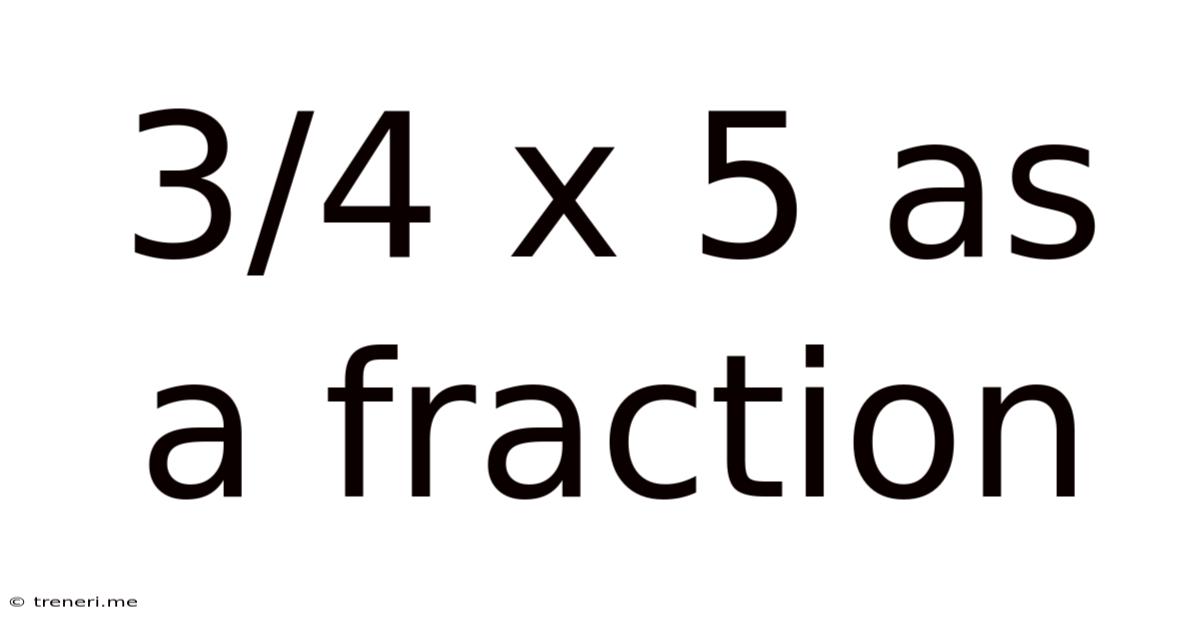
Table of Contents
3/4 x 5 as a Fraction: A Comprehensive Guide
Multiplying fractions can seem daunting at first, but with a clear understanding of the process, it becomes straightforward. This comprehensive guide will walk you through multiplying the fraction 3/4 by the whole number 5, explaining the process step-by-step and exploring various related concepts. We'll also delve into the practical applications of this type of calculation and offer tips for mastering fraction multiplication.
Understanding Fractions and Whole Numbers
Before diving into the multiplication, let's refresh our understanding of fractions and whole numbers.
Fractions: A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). The numerator indicates the number of parts you have, while the denominator indicates the total number of equal parts the whole is divided into. For example, in the fraction 3/4, 3 is the numerator and 4 is the denominator. This means we have 3 out of 4 equal parts.
Whole Numbers: Whole numbers are simply the counting numbers (0, 1, 2, 3, and so on). They represent complete units without any fractional parts. In our problem, 5 is a whole number.
Multiplying a Fraction by a Whole Number
To multiply a fraction (like 3/4) by a whole number (like 5), we follow these steps:
Step 1: Rewrite the Whole Number as a Fraction
Every whole number can be expressed as a fraction by placing the whole number over 1. So, 5 can be written as 5/1.
Step 2: Multiply the Numerators
Multiply the numerators of the two fractions together. In our case:
3 (numerator of 3/4) * 5 (numerator of 5/1) = 15
Step 3: Multiply the Denominators
Multiply the denominators of the two fractions together. In our case:
4 (denominator of 3/4) * 1 (denominator of 5/1) = 4
Step 4: Form the Resulting Fraction
Combine the results from steps 2 and 3 to create the resulting fraction:
15/4
This fraction, 15/4, is an improper fraction because the numerator (15) is larger than the denominator (4).
Converting Improper Fractions to Mixed Numbers
Improper fractions are often converted to mixed numbers for easier understanding and interpretation. A mixed number consists of a whole number and a proper fraction. To convert 15/4 to a mixed number, we perform division:
15 ÷ 4 = 3 with a remainder of 3.
The quotient (3) becomes the whole number part of the mixed number. The remainder (3) becomes the numerator of the fractional part, and the divisor (4) remains the denominator. Therefore, 15/4 is equivalent to 3 ¾.
Visualizing the Multiplication
Imagine a pizza cut into 4 equal slices. The fraction 3/4 represents 3 slices of that pizza. Multiplying by 5 means we have 5 pizzas, each with 3/4 slices. In total, we have 5 * 3 = 15 slices. Since each pizza has 4 slices, we have 15/4, or 3 ¾ pizzas.
Practical Applications
Understanding fraction multiplication is crucial in various real-life scenarios:
- Cooking and Baking: Scaling recipes up or down often involves multiplying fractions. If a recipe calls for 1/2 cup of flour and you want to double the recipe, you multiply 1/2 by 2.
- Measurement and Construction: In construction and other fields involving precise measurements, you'll frequently encounter scenarios requiring fraction multiplication for accurate calculations.
- Finance and Budgeting: Calculating percentages, interest rates, and portions of budgets often involves working with fractions.
- Data Analysis: In statistics and data analysis, fractions and their manipulations are essential for representing and interpreting data.
- Geometry and other mathematical fields: Fractions are foundational in many advanced mathematical concepts, making their mastery critical for understanding more complex topics.
Advanced Concepts and Related Topics
Let's explore some related concepts to enhance your understanding of fraction multiplication:
- Simplifying Fractions: Before and after multiplication, it's beneficial to simplify fractions by finding common factors in the numerator and denominator. For example, 6/8 can be simplified to 3/4 by dividing both the numerator and the denominator by 2.
- Multiplying More Than Two Fractions: The process extends to multiplying more than two fractions. Simply multiply all the numerators together and all the denominators together.
- Reciprocal of a Fraction: The reciprocal of a fraction is obtained by switching the numerator and denominator. For example, the reciprocal of 3/4 is 4/3. This concept is important in division of fractions.
- Fraction Division: Dividing by a fraction is the same as multiplying by its reciprocal. For instance, 3/4 ÷ 2/5 is the same as 3/4 * 5/2.
Tips for Mastering Fraction Multiplication
- Practice Regularly: The more you practice, the more comfortable you'll become with the process.
- Visual Aids: Use visual aids like diagrams or physical objects to help visualize the multiplication process.
- Break Down Complex Problems: If you face a complicated problem, break it down into smaller, more manageable steps.
- Check Your Work: Always check your answers to ensure accuracy.
- Use Online Resources: Utilize online calculators or educational websites to verify your answers and explore interactive exercises.
Conclusion
Multiplying fractions, such as 3/4 x 5, is a fundamental mathematical skill with broad applications. By understanding the steps involved and practicing regularly, you can confidently tackle fraction multiplication problems and apply this knowledge to various real-world situations. Remember to convert improper fractions to mixed numbers for easier interpretation and to simplify fractions whenever possible for efficiency. With consistent practice and a clear understanding of the underlying concepts, mastering fraction multiplication will significantly enhance your mathematical abilities. This foundational skill empowers you to confidently approach more complex mathematical challenges and successfully apply fractional calculations in everyday life. From baking a cake to analyzing financial data, the ability to multiply fractions is a valuable asset that will serve you well in numerous contexts.
Latest Posts
Latest Posts
-
What Is The Next Perfect Square After 36
May 10, 2025
-
Cuantos Dias Han Pasado Del 2024
May 10, 2025
-
30 Days From Nov 8 2024
May 10, 2025
-
Time In A Half For 18
May 10, 2025
-
98 Rounded To The Nearest Ten
May 10, 2025
Related Post
Thank you for visiting our website which covers about 3/4 X 5 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.