3/5 + 1/4 As A Fraction
Treneri
May 14, 2025 · 5 min read
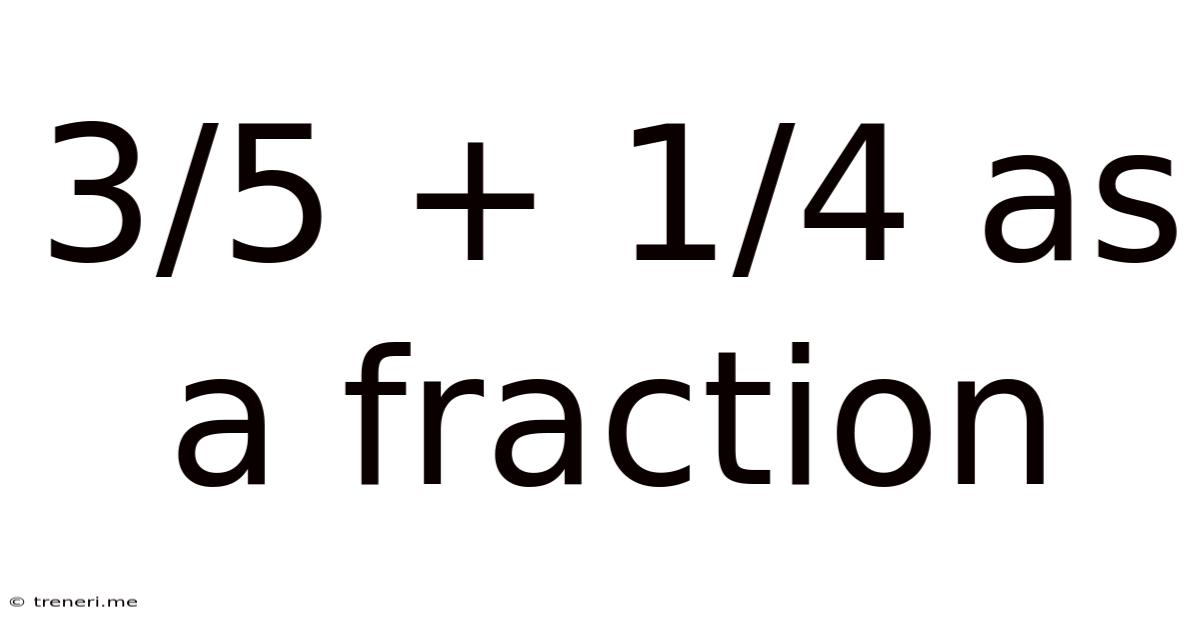
Table of Contents
3/5 + 1/4 as a Fraction: A Comprehensive Guide
Adding fractions might seem like a simple arithmetic task, but mastering it is crucial for various mathematical applications. This comprehensive guide will delve into the process of adding 3/5 and 1/4, explaining the underlying principles and providing a step-by-step solution. We'll also explore common misconceptions and offer practical tips to improve your fraction addition skills. By the end, you'll not only understand how to solve this specific problem but also possess a solid foundation for tackling any fraction addition challenge.
Understanding the Basics of Fraction Addition
Before tackling the problem of 3/5 + 1/4, let's refresh our understanding of fraction fundamentals. A fraction represents a part of a whole. It's composed of two key elements:
- Numerator: The top number represents the number of parts you have.
- Denominator: The bottom number indicates the total number of equal parts the whole is divided into.
Adding fractions involves combining these parts. However, a crucial rule governs fraction addition: you can only add fractions with the same denominator. This is because you need a common unit of measurement to accurately combine the parts.
Finding the Least Common Denominator (LCD)
Since 3/5 and 1/4 have different denominators (5 and 4), we must find their least common denominator (LCD). The LCD is the smallest number that both 5 and 4 can divide into evenly. There are several ways to find the LCD:
Method 1: Listing Multiples
List the multiples of each denominator until you find a common multiple:
- Multiples of 5: 5, 10, 15, 20, 25, 30...
- Multiples of 4: 4, 8, 12, 16, 20, 24...
The smallest common multiple is 20. Therefore, the LCD of 5 and 4 is 20.
Method 2: Prime Factorization
This method is particularly useful for larger denominators. Break down each denominator into its prime factors:
- 5: 5 (5 is a prime number)
- 4: 2 x 2
The LCD is found by taking the highest power of each prime factor present in the denominators: 2² x 5 = 20.
Converting Fractions to Equivalent Fractions
Once we have the LCD (20), we need to convert both 3/5 and 1/4 into equivalent fractions with a denominator of 20. To do this, we multiply both the numerator and the denominator of each fraction by the appropriate factor:
-
3/5: To get a denominator of 20, we multiply both the numerator and denominator by 4 (20/5 = 4): (3 x 4) / (5 x 4) = 12/20
-
1/4: To get a denominator of 20, we multiply both the numerator and denominator by 5 (20/4 = 5): (1 x 5) / (4 x 5) = 5/20
Adding the Fractions
Now that both fractions have the same denominator (20), we can add them by simply adding the numerators and keeping the denominator the same:
12/20 + 5/20 = (12 + 5) / 20 = 17/20
Simplifying the Fraction (If Necessary)
In this case, 17/20 is already in its simplest form. A fraction is in its simplest form when the greatest common divisor (GCD) of the numerator and denominator is 1. Since 17 is a prime number and doesn't divide evenly into 20, we cannot simplify further.
The Complete Solution: 3/5 + 1/4 = 17/20
Therefore, the sum of 3/5 and 1/4 is 17/20.
Common Mistakes to Avoid
Several common mistakes can hinder accurate fraction addition:
- Forgetting to find the LCD: This is the most frequent error. Always ensure your fractions have the same denominator before adding.
- Incorrectly converting to equivalent fractions: Double-check your multiplication when converting fractions to the LCD. Remember to multiply both the numerator and the denominator.
- Adding the denominators: Only the numerators are added; the denominator remains the same.
- Failing to simplify: Always simplify your answer to its lowest terms for a complete and accurate solution.
Practical Tips for Mastering Fraction Addition
- Practice regularly: Consistent practice is key to mastering any mathematical concept. Work through various examples, gradually increasing the complexity of the fractions.
- Visual aids: Use diagrams or models (like pie charts) to visualize the addition process. This can make the concept more intuitive.
- Use online resources: Many websites and apps offer interactive exercises and tutorials on fraction addition.
- Break down complex problems: If you encounter a problem with multiple fractions, break it down into smaller, manageable steps.
Beyond the Basics: Expanding Your Knowledge
The principles of adding fractions extend to more complex scenarios, including:
- Adding mixed numbers: Mixed numbers (a whole number and a fraction, e.g., 2 1/2) require converting them to improper fractions before adding.
- Adding fractions with variables: Algebra introduces fractions with variables, requiring similar steps, but with algebraic manipulation.
- Adding more than two fractions: The process remains consistent; find the LCD for all the fractions involved and then add the numerators.
Mastering fraction addition is a fundamental skill. By understanding the underlying principles, avoiding common mistakes, and practicing regularly, you'll build a strong foundation for more advanced mathematical concepts. Remember, the key is to find the least common denominator, convert to equivalent fractions, add the numerators, and simplify the result. With consistent effort, you'll confidently tackle any fraction addition problem that comes your way. The journey to mastering fractions is rewarding, opening doors to a deeper understanding of mathematics and its many applications in everyday life.
Latest Posts
Latest Posts
-
3 Out Of 50 As A Percentage
May 15, 2025
-
How To Find Perimeter Of A Octagon
May 15, 2025
-
0 16666 As A Fraction In Simplest Form
May 15, 2025
-
Circumference Of A 12 Foot Circle
May 15, 2025
-
How To Turn A Number Into A Radical
May 15, 2025
Related Post
Thank you for visiting our website which covers about 3/5 + 1/4 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.