3/5 Divided By 1/6 As A Fraction
Treneri
May 12, 2025 · 5 min read
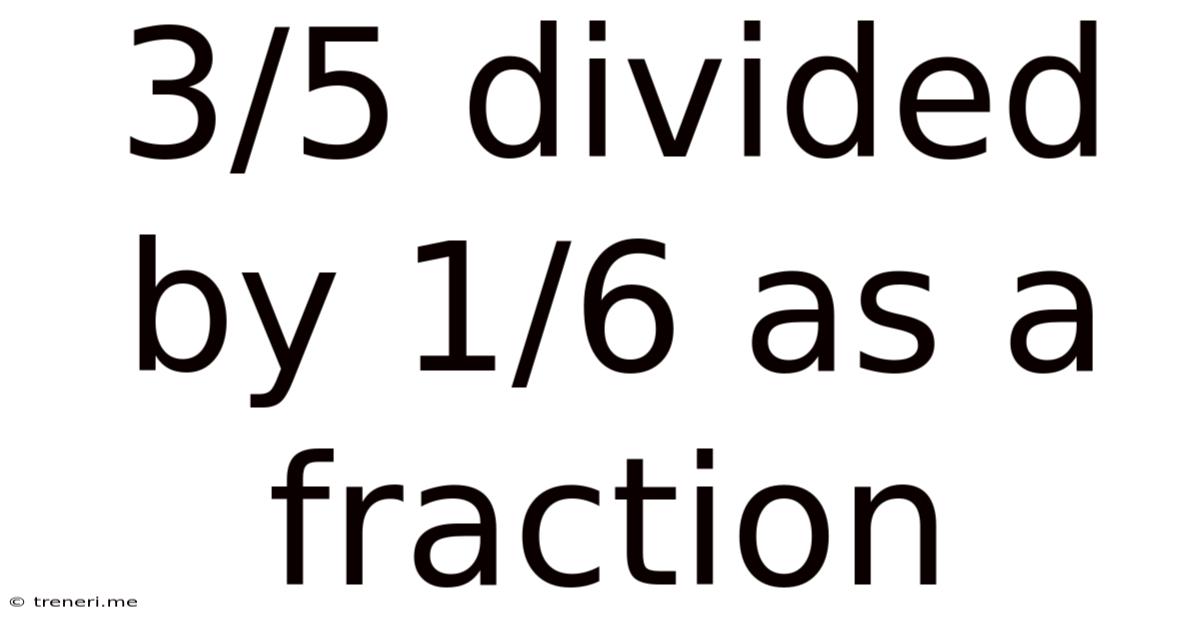
Table of Contents
3/5 Divided by 1/6 as a Fraction: A Comprehensive Guide
Dividing fractions can seem daunting, but with a clear understanding of the process, it becomes straightforward. This comprehensive guide will walk you through dividing 3/5 by 1/6, explaining the underlying principles and providing various methods to arrive at the solution. We'll explore the concept of reciprocals, demonstrate the step-by-step calculations, and delve into practical applications to solidify your understanding.
Understanding Fraction Division
Before diving into the specific problem of 3/5 divided by 1/6, let's establish a foundational understanding of fraction division. The core principle revolves around the concept of reciprocals.
What is a Reciprocal?
The reciprocal of a fraction is simply the fraction flipped upside down. For instance, the reciprocal of 1/6 is 6/1 (or simply 6). This concept is crucial because dividing by a fraction is equivalent to multiplying by its reciprocal.
This seemingly simple switch transforms a division problem into a multiplication problem, which is generally easier to manage.
The Rule of Fraction Division
The fundamental rule for dividing fractions is as follows:
To divide a fraction by another fraction, multiply the first fraction by the reciprocal of the second fraction.
This rule forms the bedrock of solving our problem: 3/5 divided by 1/6.
Solving 3/5 Divided by 1/6
Now, let's apply the rule to solve our problem: 3/5 ÷ 1/6
Step 1: Identify the Reciprocal
The reciprocal of 1/6 is 6/1 or simply 6.
Step 2: Rewrite as Multiplication
Following the rule, we rewrite the division problem as a multiplication problem:
3/5 × 6/1
Step 3: Perform the Multiplication
Multiply the numerators (top numbers) together and the denominators (bottom numbers) together:
(3 × 6) / (5 × 1) = 18/5
Step 4: Simplify the Result (If Necessary)
In this case, 18/5 is an improper fraction (the numerator is larger than the denominator). We can simplify it into a mixed number:
18 ÷ 5 = 3 with a remainder of 3. Therefore, 18/5 can be written as 3 3/5.
Therefore, 3/5 divided by 1/6 equals 18/5 or 3 3/5.
Alternative Methods and Visualizations
While the reciprocal method is the most efficient, let's explore alternative approaches to reinforce understanding.
Visual Representation using Area Models
Imagine a rectangle representing one whole unit. Divide this rectangle into 5 equal parts, and shade 3 of them to represent 3/5. Now, consider dividing this shaded area into 6 equal parts. Each of these smaller parts would represent (3/5) / 6 which is equivalent to (3/5) * (1/6) and simplifies to 3/30, or 1/10. Thinking in terms of area models will help you to visualize the multiplication and division.
Using Decimal Conversion
We can convert the fractions to decimals and then perform the division:
- 3/5 = 0.6
- 1/6 ≈ 0.1667
Then, 0.6 ÷ 0.1667 ≈ 3.6
While this approach yields an approximate answer due to rounding in the decimal conversion of 1/6, it provides an alternative perspective on the problem.
Understanding the "Why" Behind the Reciprocal Method
Why does flipping the second fraction work? Let's consider a simpler example: 2 ÷ 1/2. This asks, "How many halves are there in 2?" Intuitively, we know there are four halves in two. Notice that this is equivalent to 2 * 2 = 4. This illustrates the essence of the reciprocal method – it essentially counts how many times the divisor fits into the dividend.
Real-World Applications of Fraction Division
Fraction division isn't just an abstract mathematical concept; it has numerous practical applications in everyday life. Consider these examples:
-
Cooking and Baking: Scaling recipes up or down frequently involves dividing fractions. If a recipe calls for 1/2 cup of flour and you want to make only 1/3 of the recipe, you need to calculate (1/2) ÷ 3 = 1/6 cup of flour.
-
Sewing and Tailoring: Cutting fabric accurately requires precise measurements, often involving fraction division. If you need to divide a piece of fabric measuring 3/4 of a yard into 5 equal strips, you would calculate (3/4) ÷ 5 = 3/20 yards for each strip.
-
Construction and Engineering: Dividing materials for projects necessitates fraction division. Imagine dividing a 5/8 inch piece of wood into 3 equal pieces. Each piece would measure (5/8) ÷ 3 = 5/24 inches.
-
Data Analysis: Many situations in data analysis involve calculating proportions and ratios which often use fraction division.
Advanced Concepts and Extensions
While we've focused on dividing simple fractions, the principles extend to more complex scenarios:
-
Dividing Mixed Numbers: To divide mixed numbers, first convert them into improper fractions, then apply the reciprocal method.
-
Dividing Fractions with Variables: The same principles apply when dealing with fractions containing variables (algebraic expressions).
-
Complex Fractions: Complex fractions involve fractions within fractions, requiring multiple steps of simplification.
Conclusion: Mastering Fraction Division
Dividing fractions, while initially appearing complex, simplifies significantly with a solid grasp of reciprocals and the fundamental rule. By understanding the underlying principles and practicing various methods, you can confidently tackle fraction division problems in diverse contexts. Remember to always simplify your final answer, and don't hesitate to utilize visual aids or alternative approaches to solidify your understanding. With consistent practice, fraction division will become second nature, empowering you to tackle real-world challenges that require this essential mathematical skill. This comprehensive guide aims to provide you with the necessary tools and understanding to confidently perform fraction division. Practice consistently, explore diverse problem types, and you will master this important mathematical concept.
Latest Posts
Latest Posts
-
What Is 12 4 In Simplest Form
May 13, 2025
-
Calories Burned In An Hour Of Swimming
May 13, 2025
-
Convert Liters Per Min To Gpm
May 13, 2025
-
How Many Gallons Are In 7 L
May 13, 2025
-
How Do You Calculate The Volume Of A Room
May 13, 2025
Related Post
Thank you for visiting our website which covers about 3/5 Divided By 1/6 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.