3/8 + 1/3 As A Fraction
Treneri
May 13, 2025 · 5 min read
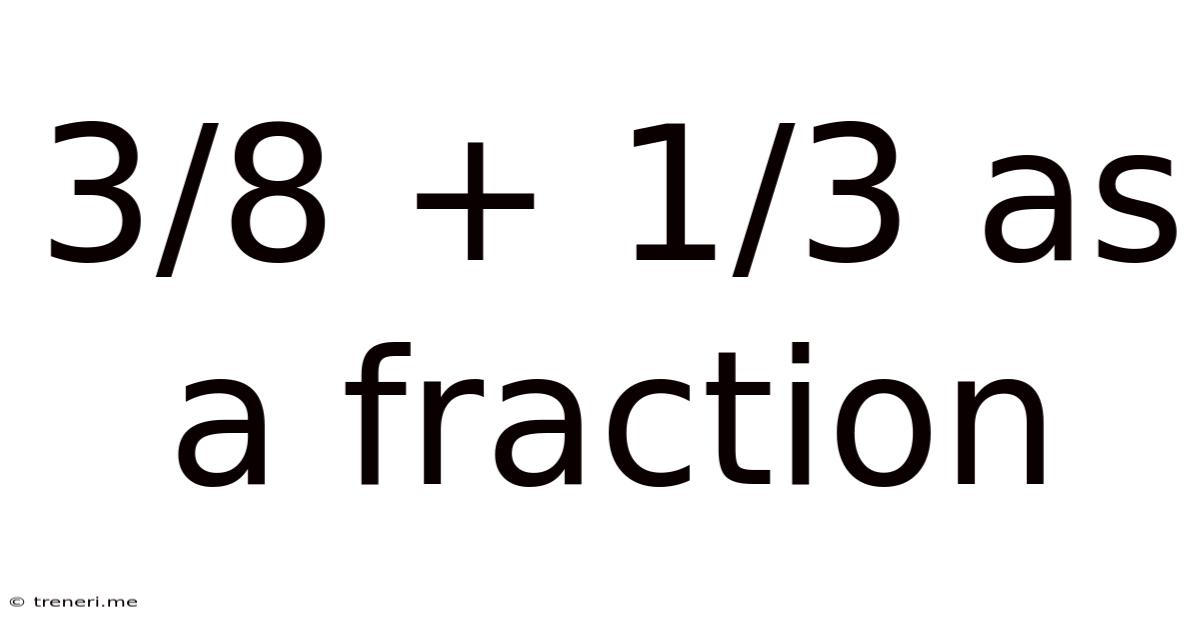
Table of Contents
3/8 + 1/3 as a Fraction: A Comprehensive Guide
Adding fractions might seem like a simple arithmetic task, but understanding the underlying principles and mastering the techniques is crucial for various applications in mathematics and beyond. This comprehensive guide delves into the addition of 3/8 and 1/3, explaining the process step-by-step, exploring different approaches, and highlighting the importance of simplifying fractions to their lowest terms. We'll also touch upon real-world applications where this seemingly basic calculation finds its use.
Understanding Fractions
Before we tackle the addition of 3/8 and 1/3, let's refresh our understanding of fractions. A fraction represents a part of a whole. It consists of two main components:
- Numerator: The top number represents the number of parts we have.
- Denominator: The bottom number represents the total number of equal parts the whole is divided into.
For example, in the fraction 3/8, 3 is the numerator and 8 is the denominator. This means we have 3 out of 8 equal parts.
Adding Fractions with Different Denominators
Adding fractions with the same denominator is straightforward; simply add the numerators and keep the denominator the same. However, adding fractions with different denominators, like 3/8 and 1/3, requires a crucial step: finding a common denominator.
A common denominator is a number that is a multiple of both denominators. The most efficient common denominator is the least common multiple (LCM). Let's find the LCM of 8 and 3.
Finding the Least Common Multiple (LCM)
There are several ways to find the LCM of two numbers. Here are two common methods:
-
Listing Multiples: List the multiples of each number until you find a common multiple.
- Multiples of 8: 8, 16, 24, 32, 40...
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27...
- The least common multiple is 24.
-
Prime Factorization: Break down each number into its prime factors. The LCM is the product of the highest powers of all prime factors present in the numbers.
- 8 = 2 x 2 x 2 = 2³
- 3 = 3
- LCM = 2³ x 3 = 24
Converting Fractions to Equivalent Fractions
Now that we have the LCM (24), we need to convert both fractions, 3/8 and 1/3, into equivalent fractions with a denominator of 24. We do this by multiplying both the numerator and the denominator of each fraction by the appropriate factor.
-
For 3/8: To get a denominator of 24, we multiply both the numerator and denominator by 3 (because 8 x 3 = 24). This gives us (3 x 3) / (8 x 3) = 9/24.
-
For 1/3: To get a denominator of 24, we multiply both the numerator and denominator by 8 (because 3 x 8 = 24). This gives us (1 x 8) / (3 x 8) = 8/24.
Adding the Equivalent Fractions
Now that both fractions have the same denominator, we can add them:
9/24 + 8/24 = (9 + 8) / 24 = 17/24
Therefore, 3/8 + 1/3 = 17/24.
Simplifying Fractions
The final step is to simplify the resulting fraction to its lowest terms. A fraction is in its lowest terms when the greatest common divisor (GCD) of the numerator and denominator is 1. In this case, the GCD of 17 and 24 is 1, meaning the fraction 17/24 is already in its simplest form.
Alternative Methods
While the LCM method is generally preferred for its efficiency, other methods can also be used to add fractions with different denominators. One such method involves finding a common denominator by simply multiplying the two denominators together. However, this method often results in a larger denominator than necessary, requiring further simplification.
For example, multiplying the denominators of 3/8 and 1/3 gives us a common denominator of 24 (8 x 3 = 24). This leads to the same result as the LCM method, but it might involve more simplification later on if a larger common multiple is chosen.
Real-World Applications
Adding fractions isn't just an abstract mathematical concept; it has many practical applications in everyday life. Here are a few examples:
-
Cooking and Baking: Recipes often require fractions of ingredients. Adding fractions helps determine the total amount of an ingredient needed when combining different recipes or adjusting serving sizes.
-
Construction and Engineering: Accurate measurements are crucial in construction and engineering. Adding fractions ensures precise calculations for distances, material quantities, and other vital aspects of a project.
-
Finance: Managing finances often involves dealing with fractions of money (cents). Adding fractions is essential for calculating budgets, debts, and investment returns.
-
Data Analysis: Representing and manipulating data often involves fractions and proportions. Adding fractions helps in analyzing data sets and drawing meaningful conclusions.
Conclusion
Adding fractions like 3/8 and 1/3 might seem trivial at first glance, but a deep understanding of the process, including finding the least common multiple, converting to equivalent fractions, and simplifying the result, is vital for various mathematical and real-world applications. Mastering these techniques builds a strong foundation for more advanced mathematical concepts and problem-solving skills. By using the LCM method, we efficiently arrive at the simplified answer of 17/24, demonstrating the importance of using the most efficient mathematical tools at our disposal. Remember to always simplify your fractions to their lowest terms for clarity and accuracy. Practice is key to developing fluency and confidence in performing these calculations. The more you practice, the easier and more intuitive the process will become.
Latest Posts
Latest Posts
-
How Many Ounces Is In 3 Pounds
May 13, 2025
-
What Is A 60 As A Grade
May 13, 2025
-
Cuanto Es 100 Gramos En Cups
May 13, 2025
-
How Long Is 44 Days In Months
May 13, 2025
-
A Wave Of Frequency Of 1000 Hertz Vibrates At
May 13, 2025
Related Post
Thank you for visiting our website which covers about 3/8 + 1/3 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.