3 Is 1 Of What Amount
Treneri
May 14, 2025 · 5 min read
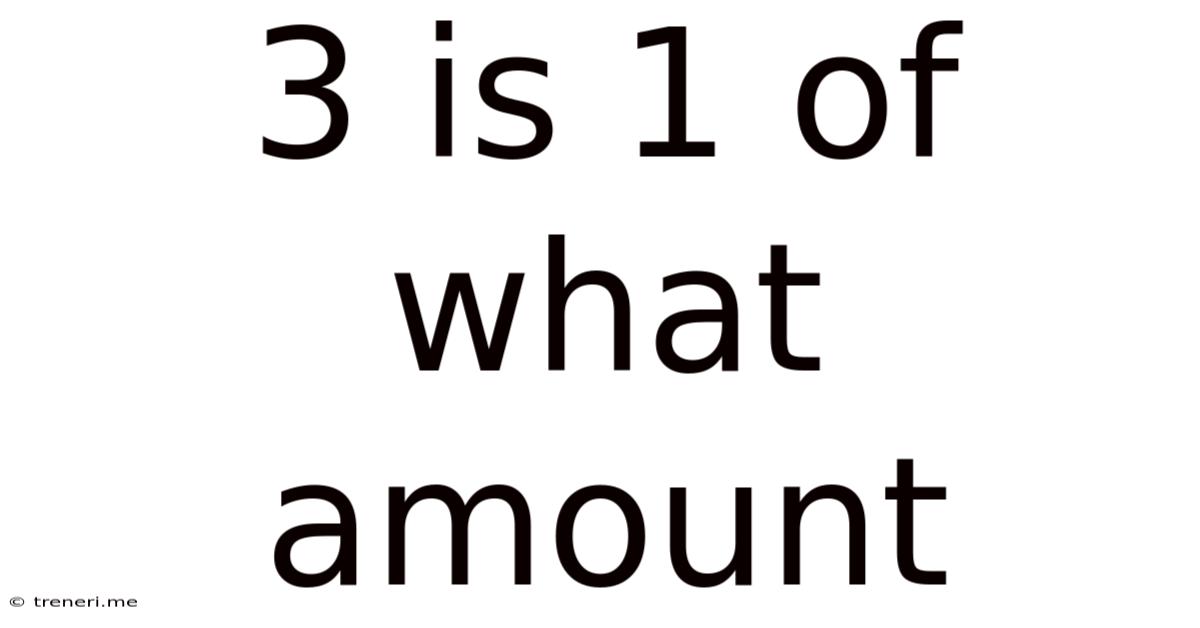
Table of Contents
3 is 1/x of what amount? Solving Percentage Problems
Understanding percentages is a fundamental skill applicable across numerous fields, from everyday budgeting to complex financial analyses. This article delves into the question: "3 is 1/x of what amount?" We'll explore different approaches to solving this type of problem, highlighting the underlying mathematical principles and providing practical examples to solidify your understanding. We'll also cover related concepts and offer tips for tackling similar percentage problems.
Deconstructing the Problem: Understanding the Fundamentals
The core of the problem lies in translating the verbal statement "3 is 1/x of what amount?" into a mathematical equation. Let's break it down step by step:
- "3 is": This translates directly to "3 =".
- "1/x of": This represents a fraction of an unknown quantity. "Of" in mathematical terms means multiplication. So, "1/x of what amount" becomes (1/x) * y, where 'y' is the unknown amount we're trying to find.
Therefore, the complete equation becomes:
3 = (1/x) * y
This equation highlights the key variables:
- 3: The known value or part.
- x: A fraction representing the percentage part.
- y: The unknown total amount (the "what amount" part).
Solving for 'y' (The Unknown Amount): Different Approaches
Depending on the value of 'x', we can solve for 'y' using several methods. Let's explore some scenarios:
Scenario 1: Solving when 'x' is known
If 'x' is a known number, the solution is straightforward. Let's assume x = 3. Our equation now becomes:
3 = (1/3) * y
To solve for 'y', we follow these steps:
-
Multiply both sides by 3: This eliminates the fraction on the right side. 3 * 3 = (1/3) * y * 3 which simplifies to 9 = y.
-
Therefore, y = 9. In this case, 3 is one-third of 9.
Scenario 2: Solving when 'x' is unknown, but the relationship is given
Sometimes, the problem might state the relationship between 3 and the unknown amount in different terms. For example:
"3 represents 25% of what amount?"
Here, the fraction 1/x is implicitly defined as 25%, or 0.25. The equation becomes:
3 = 0.25 * y
To solve:
-
Divide both sides by 0.25: 3 / 0.25 = y
-
Therefore, y = 12. 3 is 25% of 12.
Scenario 3: Solving when 'x' is represented by another variable or expression
The complexity increases if 'x' is itself an expression or another variable. For example:
"3 is 1/(2z + 1) of what amount?"
Here, 'x' is represented by (2z + 1). The equation becomes:
3 = [1/(2z + 1)] * y
Solving this requires knowing the value of 'z'. If z = 1, the equation simplifies to:
3 = (1/3) * y
Following the steps in Scenario 1, we get y = 9.
Practical Applications and Real-World Examples
Understanding this type of percentage problem is crucial in many real-world situations:
-
Finance: Calculating interest earned, determining discounts, analyzing investment returns, and understanding loan payments. For example, if you earned $3 interest and that's 1/10th of your total interest earnings, you can easily calculate your total interest earnings.
-
Business: Analyzing sales figures (e.g., determining the total sales if a specific product accounts for a certain percentage of overall revenue), managing inventory, and calculating profit margins.
-
Everyday Life: Determining tips, calculating sale prices, understanding discounts offered, splitting bills, and working with recipes (e.g., scaling a recipe up or down). For example, if 3 cups of flour make up 1/4 of a recipe, you can calculate the total amount of flour needed.
-
Science: Analyzing data sets, understanding proportions in experiments, calculating concentrations, and interpreting statistical results.
-
Data Analysis: Calculating percentages in various statistical representations. A sample of 3 respondents may represent 1/10th of the total surveyed.
Expanding Your Understanding: Related Percentage Concepts
To master percentage problems, it's beneficial to understand related concepts:
-
Percentage Increase/Decrease: Calculating the increase or decrease in a value relative to its original amount.
-
Percentage Change: Determining the overall percentage change between two values.
-
Compound Interest: Calculating interest that earns interest over time.
-
Ratios and Proportions: Understanding the relationship between two or more quantities.
Tips for Solving Percentage Problems
-
Identify the known variables: Carefully read the problem statement to determine the given information (such as the percentage, the part, or the total).
-
Translate the problem into an equation: Use mathematical symbols to represent the words in the problem.
-
Solve the equation: Utilize algebraic techniques to isolate and solve for the unknown variable.
-
Check your answer: Once you have solved for the unknown, check your answer by plugging it back into the original equation to ensure it satisfies the conditions of the problem.
-
Practice regularly: The more you practice solving percentage problems, the more confident and proficient you will become. Try working through various examples with different levels of complexity.
Conclusion: Mastering Percentage Calculations
The seemingly simple question "3 is 1/x of what amount?" reveals a fundamental aspect of percentage calculations. By understanding the underlying mathematical principles and applying the various solution approaches outlined in this article, you can confidently tackle a wide range of percentage problems in diverse contexts. Remember to break down the problem into smaller steps, translate the words into equations, and practice regularly to solidify your skills. The ability to solve percentage problems is a powerful tool that enhances your analytical skills and provides a significant advantage in both academic and professional endeavors.
Latest Posts
Latest Posts
-
What Year Is 35 Years Ago
May 15, 2025
-
An Inch Is What Fraction Of A Yard
May 15, 2025
-
How Many People Does 5 Lbs Of Mashed Potatoes Feed
May 15, 2025
-
How Much Is 550 Ml Of Water In Cups
May 15, 2025
-
How Many Feet Are In 2 5 Miles
May 15, 2025
Related Post
Thank you for visiting our website which covers about 3 Is 1 Of What Amount . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.