3 Is What Percent Of 11
Treneri
May 15, 2025 · 4 min read
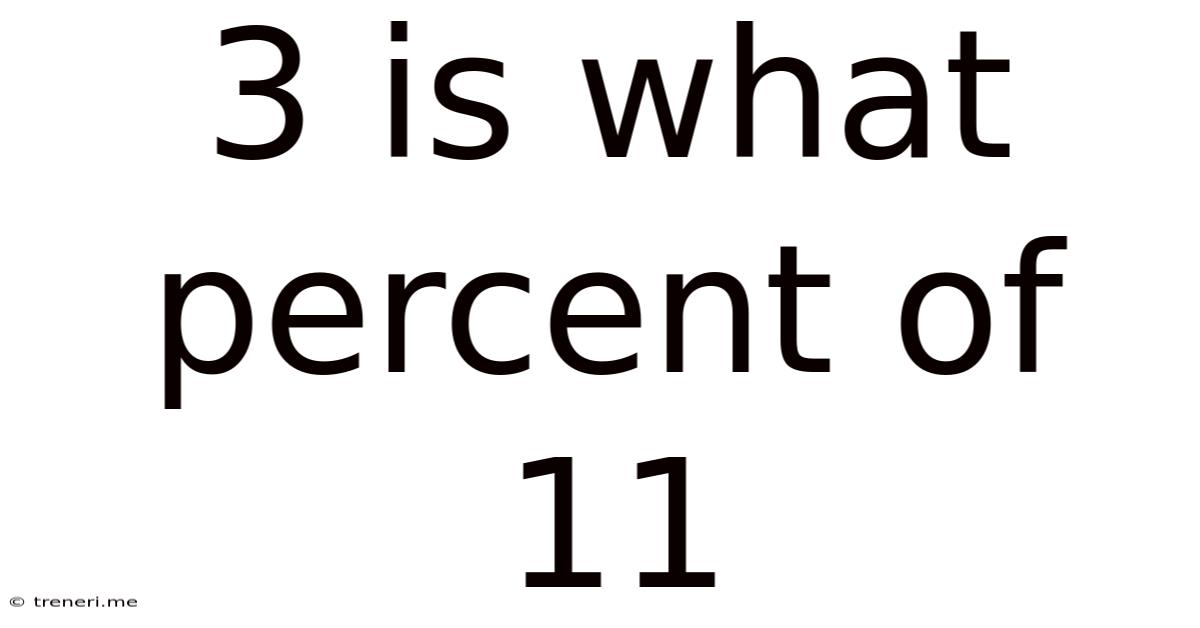
Table of Contents
3 is What Percent of 11? A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill in many aspects of life, from calculating discounts and taxes to analyzing data and understanding statistics. This article delves deep into the question, "3 is what percent of 11?", providing not only the solution but also a thorough explanation of the underlying concepts and various methods for solving similar percentage problems. We'll explore different approaches, covering both basic arithmetic and the use of proportions, ensuring you gain a solid grasp of percentage calculations.
Understanding Percentages: The Basics
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "per hundred" (from the Latin per centum). For example, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5.
When we ask, "3 is what percent of 11?", we are essentially asking: what fraction of 11 is 3, expressed as a percentage? This requires us to find the ratio of 3 to 11 and then convert that ratio into a percentage.
Method 1: Using the Percentage Formula
The most straightforward method involves using the basic percentage formula:
Part / Whole * 100% = Percentage
In our problem:
- Part: 3 (the number we want to express as a percentage)
- Whole: 11 (the total amount)
Substituting these values into the formula:
3 / 11 * 100% = Percentage
Calculating this gives us:
0.2727 * 100% ≈ 27.27%
Therefore, 3 is approximately 27.27% of 11. The slight rounding is due to the fact that the division results in a repeating decimal.
Method 2: Using Proportions
Proportions offer another effective way to solve percentage problems. A proportion sets up an equivalence between two ratios. We can set up a proportion as follows:
3 / 11 = x / 100
Where 'x' represents the percentage we want to find. This proportion states that the ratio of 3 to 11 is equal to the ratio of x to 100.
To solve for 'x', we can cross-multiply:
3 * 100 = 11 * x
300 = 11x
x = 300 / 11
x ≈ 27.27
Again, we find that 3 is approximately 27.27% of 11.
Method 3: Converting to a Decimal First
This method involves first converting the fraction 3/11 into a decimal and then multiplying by 100% to obtain the percentage.
-
Convert the fraction to a decimal: Divide 3 by 11: 3 ÷ 11 ≈ 0.2727
-
Multiply by 100%: 0.2727 * 100% ≈ 27.27%
This method provides the same result as the previous two methods, confirming the accuracy of our calculations.
Addressing Precision and Rounding
As seen in our calculations, the result of 3/11 is a repeating decimal (0.272727...). When expressing this as a percentage, we need to decide on the level of precision required. 27.27% is a commonly acceptable level of precision, but for more accurate representation, you might use more decimal places, like 27.2727%. The context of the problem dictates the appropriate level of rounding.
Real-World Applications: Examples of Percentage Calculations
Understanding percentage calculations has numerous real-world applications. Here are a few examples showcasing the practical use of these concepts:
-
Sales and Discounts: A store offers a 20% discount on an item originally priced at $50. To calculate the discount, we find 20% of $50: 0.20 * $50 = $10. The discounted price is $50 - $10 = $40.
-
Taxes and Tips: A restaurant bill is $75, and you want to leave a 15% tip. The tip amount is 0.15 * $75 = $11.25.
-
Interest Rates: If you deposit $1000 in a savings account with an annual interest rate of 5%, you'll earn 0.05 * $1000 = $50 in interest after one year.
-
Data Analysis: Percentages are crucial for interpreting data. For example, if a survey shows that 30 out of 100 respondents prefer a certain product, this is represented as 30%.
-
Grade Calculations: If you score 45 out of 60 on a test, your percentage score is (45/60) * 100% = 75%.
Expanding Your Percentage Skills
While we've focused on "3 is what percent of 11?", the principles discussed apply to a wide range of percentage problems. To further enhance your understanding, consider tackling these types of problems:
- Finding the part: What is 15% of 80?
- Finding the whole: 25 is 40% of what number?
- Finding the percentage increase or decrease: A price increased from $20 to $25. What is the percentage increase?
Mastering percentage calculations is an essential skill for success in various fields. By understanding the fundamental concepts and different methods of calculation, you'll be well-equipped to tackle a wide range of percentage problems confidently and accurately. Remember to practice regularly to solidify your understanding and build proficiency. The more you work with percentages, the easier it will become to solve these types of problems quickly and efficiently. And always remember to check your work for accuracy – it's essential in all applications of percentage calculations, from simple everyday calculations to complex financial modeling.
Latest Posts
Latest Posts
-
7 0760 Rounded To The Nearest Hundredth
May 15, 2025
-
How To Calculate Moles Of Naoh
May 15, 2025
-
1 And A Half Quarts To Cups
May 15, 2025
-
60 Days From November 11 2024
May 15, 2025
-
Number Of Weekdays In A Month
May 15, 2025
Related Post
Thank you for visiting our website which covers about 3 Is What Percent Of 11 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.