3 Out Of 24 As A Percentage
Treneri
May 09, 2025 · 4 min read
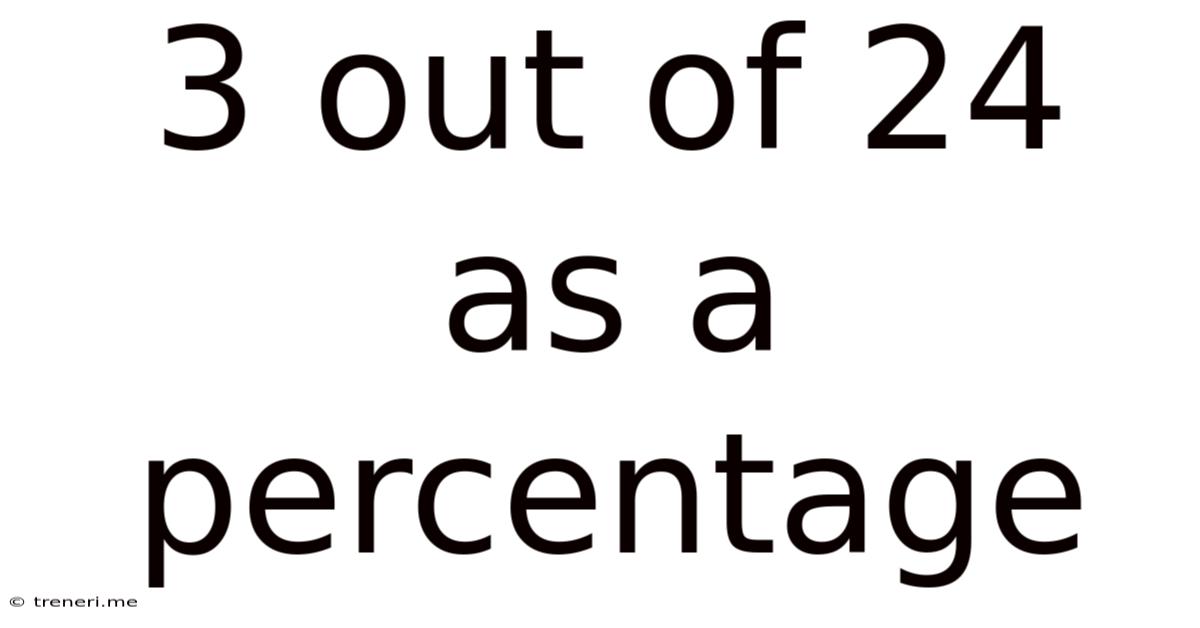
Table of Contents
3 out of 24 as a Percentage: A Comprehensive Guide
Calculating percentages is a fundamental skill applicable across numerous fields, from everyday budgeting to complex financial analysis. Understanding how to express fractions as percentages is crucial for clear communication and accurate data interpretation. This article delves into the specific calculation of "3 out of 24 as a percentage," providing a step-by-step guide, practical examples, and exploring related percentage concepts.
Understanding Percentages
A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" represents "percent," meaning "per hundred." Percentages are used to represent parts of a whole. For example, 50% means 50 out of 100, or one-half. Understanding this fundamental concept is key to solving percentage problems.
Calculating 3 out of 24 as a Percentage: The Step-by-Step Method
To calculate "3 out of 24" as a percentage, we follow these simple steps:
Step 1: Express the Fraction:
First, express the given information as a fraction. "3 out of 24" translates to the fraction 3/24.
Step 2: Convert the Fraction to a Decimal:
To convert a fraction to a decimal, divide the numerator (the top number) by the denominator (the bottom number). In this case, we divide 3 by 24:
3 ÷ 24 = 0.125
Step 3: Convert the Decimal to a Percentage:
To convert a decimal to a percentage, multiply the decimal by 100 and add the percent symbol (%).
0.125 × 100 = 12.5%
Therefore, 3 out of 24 is 12.5%.
Simplifying the Fraction (Optional but Recommended)
Before converting to a decimal, simplifying the fraction can make the calculation easier. In this case, both 3 and 24 are divisible by 3:
3/24 simplifies to 1/8
Now, converting 1/8 to a decimal:
1 ÷ 8 = 0.125
Then, converting the decimal to a percentage:
0.125 × 100 = 12.5%
This demonstrates that simplifying the fraction first doesn't alter the final percentage. However, it streamlines the calculation, especially with larger numbers.
Practical Applications of Percentage Calculations
The ability to calculate percentages has wide-ranging practical applications:
1. Business and Finance:
- Profit margins: Calculating the percentage of profit made on sales.
- Interest rates: Determining the percentage charged on loans or earned on investments.
- Sales tax: Calculating the tax amount added to purchases.
- Discount calculations: Determining the price reduction on sale items.
- Financial reporting: Analyzing financial statements and presenting data as percentages for easier understanding.
2. Everyday Life:
- Tips and gratuities: Calculating the appropriate tip amount in a restaurant.
- Shopping discounts: Determining the final price of sale items.
- Recipe scaling: Adjusting ingredient amounts based on the number of servings.
- Household budgeting: Tracking spending and savings as percentages of income.
3. Science and Statistics:
- Data analysis: Representing data as percentages for easier visualization and comparison.
- Probability calculations: Determining the likelihood of events occurring.
- Experimental results: Presenting findings as percentages to show the effectiveness of treatments or interventions.
Related Percentage Concepts
Understanding "3 out of 24 as a percentage" lays the groundwork for grasping more complex percentage calculations. Here are some related concepts:
1. Finding the Percentage Increase or Decrease:
This involves calculating the percentage change between two values. The formula is:
[(New Value - Old Value) / Old Value] × 100%
For instance, if a value increases from 20 to 25, the percentage increase is:
[(25 - 20) / 20] × 100% = 25%
2. Finding the Original Value After a Percentage Change:
If you know the new value and the percentage change, you can work backward to find the original value. This often involves using algebraic equations.
3. Calculating Percentages of a Whole:
This involves finding a specific percentage of a given number. For example, finding 20% of 150:
0.20 × 150 = 30
Advanced Percentage Calculations: Using Proportions
More complex percentage problems can be solved using proportions. A proportion is a statement that two ratios are equal. This method is particularly helpful when dealing with more intricate scenarios. For example, if you want to find what percentage 7 is of 35, you can set up a proportion:
x/100 = 7/35
Cross-multiplying, we get:
35x = 700
x = 20
Therefore, 7 is 20% of 35.
Conclusion: Mastering Percentage Calculations
Understanding how to calculate percentages, particularly simple cases like "3 out of 24," is a vital skill for navigating many aspects of life, from personal finance to professional endeavors. This article has provided a comprehensive guide, highlighting the step-by-step process, real-world applications, and related concepts. By mastering these fundamental percentage calculations, you'll enhance your analytical skills and confidently tackle more complex percentage problems in the future. Remember, practice is key to solidifying your understanding and improving your speed and accuracy. Regularly working through various percentage problems will build your confidence and mastery of this crucial mathematical skill.
Latest Posts
Latest Posts
-
4 1 2 1 1 2
May 09, 2025
-
3 4 Cup Of Milk In Oz
May 09, 2025
-
How Many Days Is 41 Hours
May 09, 2025
-
How Many Seconds Are There In 10 Mins
May 09, 2025
-
3 And 4 5 As An Improper Fraction
May 09, 2025
Related Post
Thank you for visiting our website which covers about 3 Out Of 24 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.