3 Raised To The Power Of 4
Treneri
May 09, 2025 · 5 min read
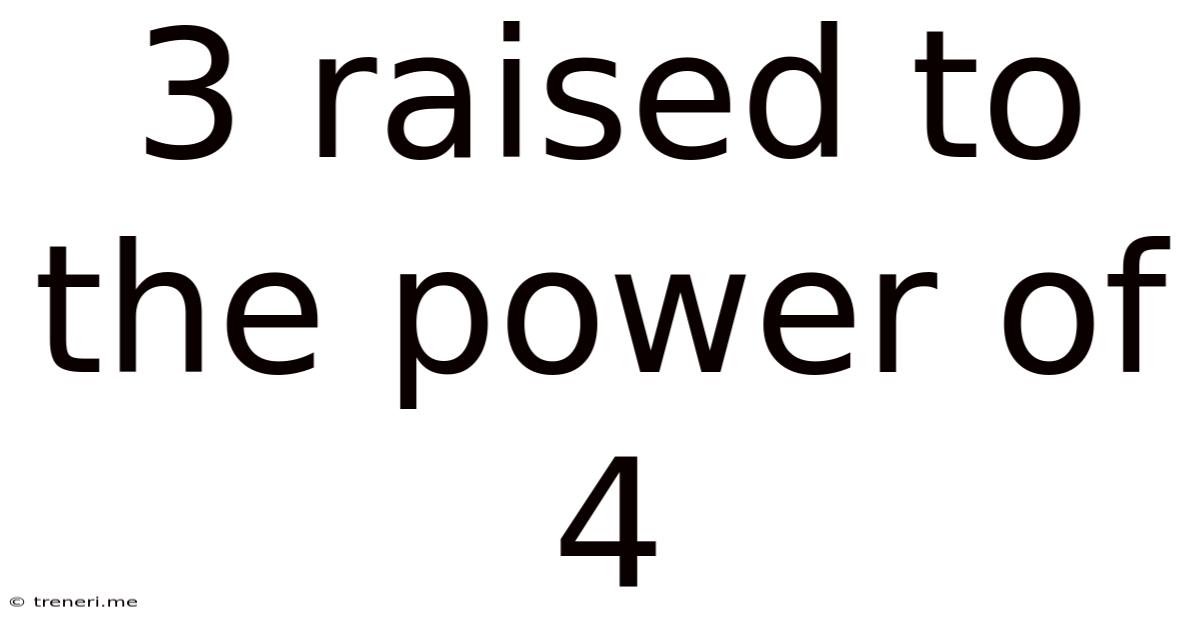
Table of Contents
3 Raised to the Power of 4: Exploring the Exponent and its Applications
The seemingly simple mathematical expression, 3 raised to the power of 4 (or 3⁴), offers a fascinating gateway into the world of exponents, their properties, and their wide-ranging applications across various fields. This exploration will delve deep into the meaning of this expression, its calculation, its significance in different mathematical contexts, and its practical uses in real-world scenarios.
Understanding Exponents: A Foundation
Before diving into the specifics of 3⁴, it's crucial to understand the fundamental concept of exponents. An exponent, also known as a power or index, indicates how many times a base number is multiplied by itself. In the general form b<sup>n</sup>, 'b' represents the base, and 'n' represents the exponent. Therefore, 3⁴ signifies that the base number 3 is multiplied by itself four times: 3 x 3 x 3 x 3.
The Simplicity and Power of Notation
Exponential notation provides a concise and efficient way to express repeated multiplication. Imagine trying to write out 3 multiplied by itself 100 times! Exponential notation simplifies this considerably, representing it as 3¹⁰⁰. This efficiency is paramount in mathematics and its various applications, from scientific calculations to computer programming.
Calculating 3⁴: Step-by-Step
Calculating 3⁴ involves a straightforward process of repeated multiplication:
- Start with the base: 3
- Multiply by the base: 3 x 3 = 9
- Multiply again: 9 x 3 = 27
- One final multiplication: 27 x 3 = 81
Therefore, 3⁴ = 81. This seemingly simple calculation forms the foundation for more complex mathematical operations and applications.
3⁴ in Different Mathematical Contexts
The number 81, the result of 3⁴, appears in various mathematical contexts, often playing a significant role in different areas:
Number Theory: Divisibility and Factors
Within number theory, 81's properties as a perfect square (9²) and a power of 3 are crucial. Understanding its factors (1, 3, 9, 27, 81) is essential for tasks like determining divisibility and solving Diophantine equations. Its significance extends to modular arithmetic and other advanced number-theoretic concepts.
Algebra: Polynomial Expressions and Equations
In algebra, 81 can be a coefficient or a constant term in polynomial expressions and equations. For example, the equation x² + 81 = 0 involves complex roots, demonstrating how seemingly simple numbers like 81 can lead to deeper mathematical explorations.
Geometry: Area Calculations and Spatial Relationships
Geometry often utilizes exponents. For instance, calculating the area of a square with a side length of 9 involves 9², which is equivalent to 3⁴ or 81. This demonstrates the practical application of exponents in real-world geometric problems. Similarly, consider the volume of a cube with side length of 3. The calculation will use 3 cubed (27), related to 3 to the power of 4.
Calculus: Derivatives and Integrals
While not directly involved in basic calculus operations, numbers derived from 3⁴ can feature in more advanced calculus problems. The number 81 itself, or expressions involving it, could represent constants of integration, coefficients, or values within function definitions.
Real-World Applications: Beyond the Classroom
The principles underlying 3⁴ and exponential calculations have far-reaching real-world applications:
Compound Interest: Financial Growth
Understanding exponents is crucial in finance, especially when calculating compound interest. The formula for compound interest involves exponents, illustrating how the power of compounding grows exponentially over time. A small initial investment growing over multiple years exemplifies the substantial impact of exponents.
Computer Science: Data Structures and Algorithms
Exponents are fundamental to computer science, particularly in algorithms related to data structures such as trees and graphs. The efficiency of many algorithms is often expressed using Big O notation, which frequently employs exponents to describe the growth of computational complexity.
Physics: Exponential Decay and Growth
Exponents frequently appear in physics, describing phenomena such as radioactive decay and population growth. Exponential decay models the decrease of a quantity over time (e.g., the decay of a radioactive substance), while exponential growth models its increase (e.g., the growth of a bacterial population). These models often involve the exponential function e<sup>x</sup>, but the underlying principles of exponents are essential to understanding their behavior.
Engineering: Scaling and Design
In engineering, scaling designs often involves exponents. For instance, increasing the size of a structure might change its strength and weight disproportionately, requiring careful consideration of scaling factors expressed using exponents.
Biology: Population Dynamics
Population growth and decay in biology can be modeled using exponential functions. Understanding how a population changes over time, influenced by factors such as birth rates and death rates, relies heavily on exponential concepts.
Exploring Further: Beyond 3⁴
While this exploration focuses on 3⁴, the principles discussed apply to other exponential expressions. Understanding exponents is fundamental to appreciating the power of mathematics in numerous applications. Further exploration might include:
- Negative exponents: Understanding what happens when the exponent is negative (e.g., 3⁻⁴ = 1/81).
- Fractional exponents: Investigating the meaning of fractional exponents (e.g., 3^(1/2) = √3).
- Complex exponents: Exploring exponents where the exponent itself is a complex number.
- Logarithms: Understanding the inverse relationship between exponents and logarithms, and their practical applications.
Conclusion: The Enduring Significance of 3⁴
The seemingly simple calculation of 3⁴ = 81 opens doors to a wealth of mathematical concepts and real-world applications. From fundamental number theory to complex scientific models, the principles of exponents are indispensable. This exploration provides a foundation for further investigation into the fascinating world of exponents and their profound impact across various disciplines. The seemingly small number 81, resulting from 3⁴, represents a significant stepping stone in understanding the far-reaching power of mathematical principles. Its significance extends far beyond simple arithmetic, revealing a deeper understanding of the interconnectedness of mathematics and the world around us.
Latest Posts
Latest Posts
-
What Is Half Of 3 1 2 Inches
May 09, 2025
-
Calculate Y Intercept From 2 Points
May 09, 2025
-
Cuantos Dias Faltan Para El 17 De Marzo
May 09, 2025
-
Cuanto Falta Para El 22 De Noviembre
May 09, 2025
-
Cuanto Es 0 Grados Centigrados En Fahrenheit
May 09, 2025
Related Post
Thank you for visiting our website which covers about 3 Raised To The Power Of 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.