3 To The Second Power Equals
Treneri
May 10, 2025 · 5 min read
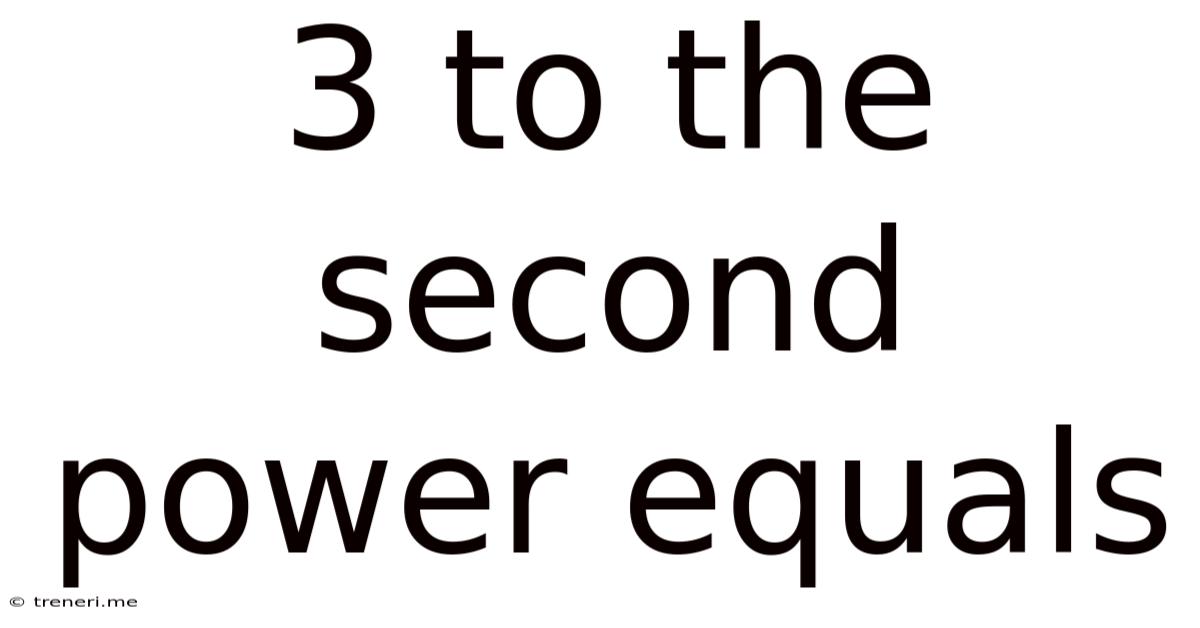
Table of Contents
3 to the Second Power Equals: Unpacking the Fundamentals of Exponents
The simple equation, "3 to the second power equals," might seem elementary, but it's a gateway to understanding a fundamental concept in mathematics: exponents. This seemingly straightforward calculation unlocks a world of mathematical possibilities, forming the basis for advanced concepts in algebra, calculus, and beyond. This comprehensive guide will delve into the meaning of 3 to the second power, explore the broader concept of exponents, and reveal their practical applications in various fields.
Understanding Exponents: A Foundation in Mathematics
Before tackling 3 to the second power, let's solidify the concept of exponents. An exponent, also known as a power or index, indicates how many times a number (the base) is multiplied by itself. It's represented as a small number written slightly above and to the right of the base. For example, in the expression 3², the '3' is the base, and the '2' is the exponent. This expression is read as "3 raised to the power of 2" or "3 squared".
The Significance of "Squared" and "Cubed"
When the exponent is 2, we often use the term "squared." This originates from the geometric concept of calculating the area of a square. A square with side length '3' has an area of 3 x 3 = 9. Similarly, when the exponent is 3, we use the term "cubed," referencing the volume of a cube. A cube with side length '3' has a volume of 3 x 3 x 3 = 27.
Calculating 3 to the Second Power
Now, let's answer the central question: 3 to the second power equals 9. This is because 3² means 3 multiplied by itself: 3 x 3 = 9.
This seemingly simple calculation is the cornerstone of numerous mathematical operations. Understanding this fundamental concept allows for easier comprehension of more complex mathematical expressions.
Expanding the Exponent Landscape: Beyond the Second Power
While 3² is a fundamental example, the concept of exponents extends far beyond the second power. Let's explore some further examples:
- 3 to the third power (3³): This means 3 x 3 x 3 = 27. As mentioned earlier, this is also known as "3 cubed."
- 3 to the fourth power (3⁴): This is 3 x 3 x 3 x 3 = 81.
- 3 to the first power (3¹): Any number raised to the power of 1 is simply itself. Therefore, 3¹ = 3.
- 3 to the zeroth power (3⁰): Any non-zero number raised to the power of 0 equals 1. Therefore, 3⁰ = 1. This might seem counterintuitive, but it's a consistent mathematical rule.
- 3 to the negative first power (3⁻¹): A negative exponent represents the reciprocal of the base raised to the positive exponent. Therefore, 3⁻¹ = 1/3.
- 3 to the negative second power (3⁻²): This is the reciprocal of 3², so 3⁻² = 1/9.
Practical Applications of Exponents: Real-World Relevance
The applications of exponents extend far beyond theoretical mathematics. They are integral to various fields, including:
-
Science: Exponents are crucial in scientific notation for representing extremely large or small numbers, such as the speed of light or the mass of an atom. For example, the speed of light is approximately 3 x 10⁸ meters per second.
-
Finance: Compound interest calculations rely heavily on exponents. The formula for compound interest involves raising the principal amount to a power representing the number of compounding periods. Understanding exponents is vital for comprehending investment growth and loan repayment schedules.
-
Computer Science: Exponents play a crucial role in algorithms and data structures. Binary numbers, the foundation of computer systems, utilize powers of 2. Furthermore, computational complexity analysis frequently involves exponential functions to describe the efficiency of algorithms.
-
Engineering: Exponential functions are used to model various phenomena in engineering, such as the decay of radioactive materials or the growth of populations. These models provide critical insights for design and optimization purposes.
-
Physics: Exponents appear in numerous physics equations, describing phenomena such as gravitational force, electric fields, and radioactive decay. Understanding exponents is crucial for interpreting and applying these equations to real-world scenarios.
Advanced Concepts: Expanding Your Understanding
Beyond the basic calculations, understanding exponents opens the door to more complex mathematical concepts:
-
Exponential Functions: These functions have the form f(x) = aˣ, where 'a' is a constant base and 'x' is the exponent. These functions are used to model growth and decay processes in various fields.
-
Logarithms: Logarithms are the inverse of exponential functions. They provide a way to solve equations involving exponents. For example, the logarithm base 3 of 9 (log₃9) is 2, because 3² = 9.
-
Polynomial Equations: Polynomial equations involve terms with variables raised to different powers. Solving these equations often requires manipulating exponents and understanding their properties.
-
Calculus: Exponents are fundamental to calculus, particularly in differentiation and integration. Understanding the rules of exponents is crucial for performing these operations effectively.
Mastering Exponents: Tips and Tricks
Here are some tips to help you master the concept of exponents:
-
Practice Regularly: The best way to solidify your understanding is to practice solving various problems involving exponents. Start with simple problems and gradually increase the complexity.
-
Understand the Rules: Learn the rules of exponents, including those involving multiplication, division, and powers of powers. These rules will make calculations much easier.
-
Utilize Online Resources: Many online resources offer tutorials, practice problems, and interactive exercises to help you master exponents.
-
Seek Help When Needed: Don't hesitate to seek help from a teacher, tutor, or online forum if you encounter difficulties.
Conclusion: The Power of Understanding
While "3 to the second power equals 9" might seem like a simple equation, its implications are far-reaching. Understanding exponents is crucial for succeeding in mathematics and various STEM fields. By mastering this foundational concept, you unlock a wealth of mathematical possibilities and gain the tools to solve complex problems across numerous disciplines. This knowledge will empower you to interpret scientific data, analyze financial trends, understand computer algorithms, and much more. The journey from a simple calculation like 3² to a comprehensive understanding of exponents demonstrates the power of building a strong mathematical foundation. So continue exploring, practicing, and expanding your knowledge; the mathematical world awaits!
Latest Posts
Latest Posts
-
What Is The Measure Of 44 50 64 92
May 10, 2025
-
How Many Days Is In Two Months
May 10, 2025
-
How Long Till 5 Pm Today
May 10, 2025
-
How To Find The Base Of Triangular Prism
May 10, 2025
-
90 Days From August 3 2024
May 10, 2025
Related Post
Thank you for visiting our website which covers about 3 To The Second Power Equals . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.