30 Is 12 Percent Of What Number
Treneri
May 11, 2025 · 4 min read
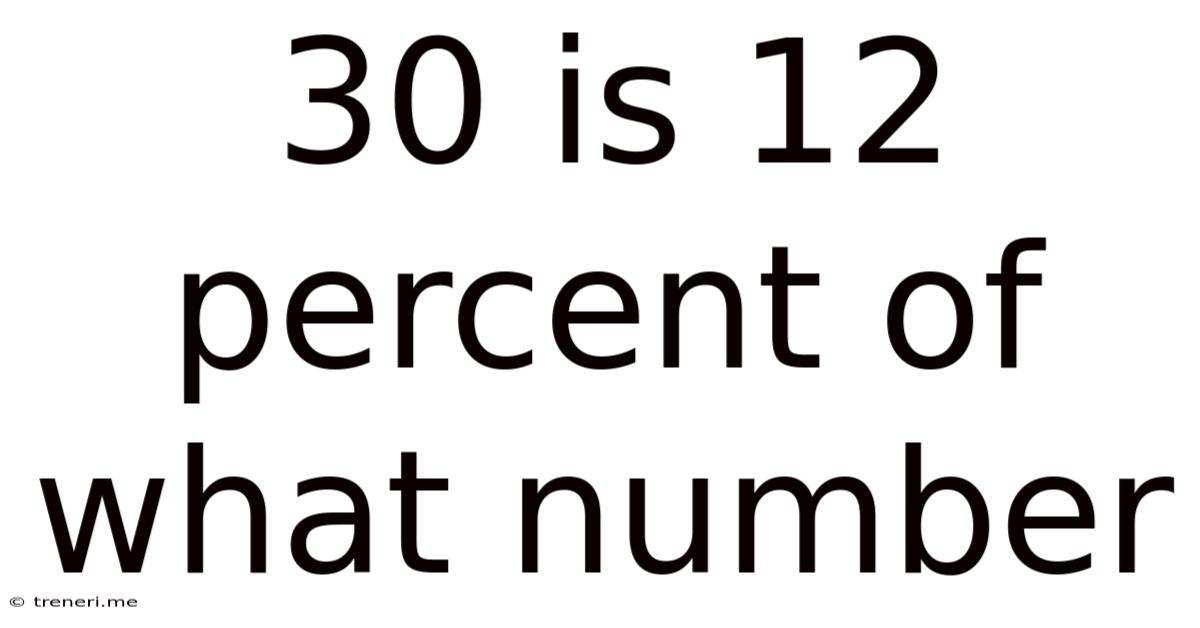
Table of Contents
30 is 12 Percent of What Number? A Comprehensive Guide to Percentage Calculations
Solving percentage problems is a fundamental skill applicable across various fields, from everyday budgeting to complex financial analyses. Understanding how to determine the base number when given a percentage and its value is crucial. This article provides a comprehensive guide to solving the problem "30 is 12 percent of what number?", explaining the process step-by-step, exploring different approaches, and highlighting practical applications.
Understanding the Basics of Percentages
Before diving into the solution, let's review the core concept of percentages. A percentage represents a fraction of 100. For instance, 12% means 12 out of 100, or 12/100, which simplifies to 3/25 as a fraction and 0.12 as a decimal.
This simple understanding allows us to translate percentage problems into algebraic equations. The fundamental equation for percentage calculations is:
(Percentage/100) * Base Number = Part
Where:
- Percentage: The rate expressed as a percentage (in our case, 12%).
- Base Number: The total value we're trying to find (the unknown in our problem).
- Part: The given portion of the base number (in our case, 30).
Solving "30 is 12 Percent of What Number?"
Now, let's apply this knowledge to our problem: "30 is 12 percent of what number?". We can translate this into an algebraic equation:
(12/100) * x = 30
Where 'x' represents the unknown base number.
To solve for 'x', we'll follow these steps:
-
Convert the percentage to a decimal: 12% = 0.12
-
Rewrite the equation: 0.12 * x = 30
-
Isolate 'x': Divide both sides of the equation by 0.12:
x = 30 / 0.12
-
Calculate the result: x = 250
Therefore, 30 is 12 percent of 250.
Alternative Methods for Solving Percentage Problems
While the above method is straightforward, several alternative approaches can be used to solve similar percentage problems. These methods offer flexibility and can be helpful depending on the context and personal preference.
Method 2: Using Proportions
Proportions provide a visual and intuitive way to solve percentage problems. We can set up a proportion:
12/100 = 30/x
This proportion states that the ratio of 12 to 100 is equal to the ratio of 30 to the unknown number (x). Cross-multiplying gives us:
12x = 3000
Dividing both sides by 12 yields:
x = 250
This confirms our previous result.
Method 3: Using the Percentage Formula Rearranged
We can rearrange the basic percentage formula to directly solve for the base number:
Base Number = (Part / Percentage) * 100
Plugging in our values:
Base Number = (30 / 12) * 100 = 250
This method efficiently calculates the base number without requiring multiple steps.
Practical Applications of Percentage Calculations
Understanding percentage calculations is essential in various real-world scenarios:
1. Finance and Budgeting:
- Calculating interest: Determining the principal amount based on interest earned or owed.
- Analyzing investment returns: Understanding the growth or loss of investments expressed as percentages.
- Tracking expenses: Calculating the percentage of income spent on different categories.
- Discount calculations: Determining the original price of an item given a discounted price and discount percentage.
2. Retail and Sales:
- Calculating markups and margins: Determining the selling price of a product based on cost and desired profit margin.
- Analyzing sales performance: Tracking sales growth or decline expressed as percentages.
- Applying discounts and sales tax: Calculating final prices considering discounts and taxes.
3. Science and Statistics:
- Data analysis: Representing data as percentages to compare different groups or categories.
- Calculating probabilities: Expressing probabilities as percentages.
- Analyzing experimental results: Expressing results as percentages to illustrate significance.
4. Everyday Life:
- Calculating tips: Determining the appropriate tip amount in restaurants based on a percentage of the bill.
- Understanding tax rates: Calculating the amount of tax owed based on income and tax rates.
- Comparing prices: Determining which product offers better value based on price and quantity.
Beyond the Basics: More Complex Percentage Problems
While the problem "30 is 12 percent of what number?" is relatively straightforward, percentage problems can become more complex. Consider these examples:
-
Finding the percentage increase or decrease: Calculating the percentage change between two values. This involves subtracting the initial value from the final value, dividing the result by the initial value, and multiplying by 100.
-
Calculating compound interest: This involves calculating interest on both the principal amount and accumulated interest over multiple periods.
-
Solving problems involving multiple percentages: These might involve calculating successive discounts or combining different percentage changes.
Mastering basic percentage calculations like the one presented in this article forms the foundation for solving these more advanced problems. With practice and a strong understanding of the underlying principles, you'll be able to confidently tackle a wide range of percentage problems in various contexts.
Conclusion: Mastering Percentage Calculations for Success
The ability to solve percentage problems efficiently is a valuable skill applicable in numerous areas of life. This article has demonstrated multiple approaches to solving the problem "30 is 12 percent of what number?", providing a step-by-step guide and exploring various practical applications. By understanding the fundamental concepts and practicing different methods, you can build confidence in tackling percentage calculations and harness their power for success in both personal and professional endeavors. Remember, practice is key! The more you work with percentages, the more comfortable and proficient you'll become. Don't hesitate to explore additional resources and practice problems to further solidify your understanding.
Latest Posts
Latest Posts
-
6 Pints Equals How Many Gallons
May 12, 2025
-
209 Rounded To The Nearest Ten
May 12, 2025
-
What Angle Is A 5 12 Pitch Roof
May 12, 2025
-
How Many Kg Is 101 Pounds
May 12, 2025
-
Compute The Volume Of The Right Square Pyramid Shown
May 12, 2025
Related Post
Thank you for visiting our website which covers about 30 Is 12 Percent Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.