32 Is What Percent Of 200
Treneri
May 10, 2025 · 5 min read
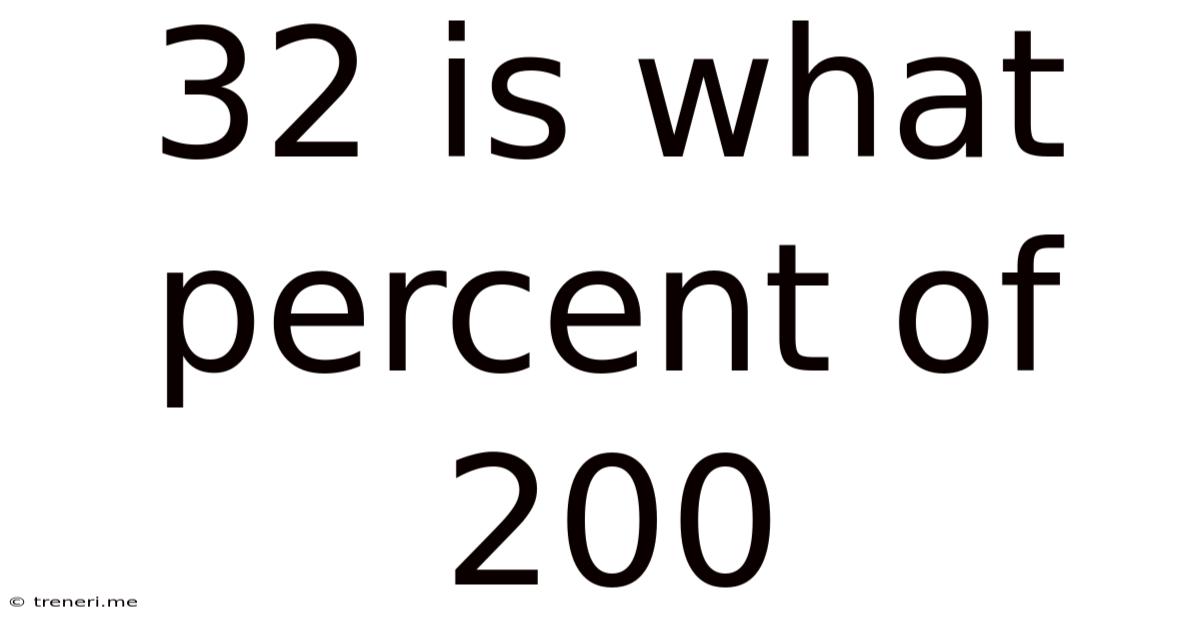
Table of Contents
32 is What Percent of 200? A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill in various aspects of life, from calculating discounts and tips to analyzing financial data and understanding statistics. This comprehensive guide will delve into the question, "32 is what percent of 200?", providing not just the answer but a thorough explanation of the process, related concepts, and practical applications. We'll explore different methods of calculation, address potential common mistakes, and offer advanced insights into percentage problems.
Understanding the Fundamentals of Percentages
Before we tackle the specific problem, let's solidify our understanding of percentages. A percentage is simply a fraction expressed as a part of 100. The symbol "%" signifies "per hundred" or "out of 100". For instance, 50% represents 50 out of 100, which is equivalent to ½ or 0.5 in decimal form.
Key Concepts:
- Part: This is the number that represents a portion of the whole. In our example, 32 is the part.
- Whole: This is the total amount or the complete value. In our problem, 200 is the whole.
- Percentage: This is the fraction of the whole expressed as a part of 100. This is what we need to calculate.
Calculating "32 is What Percent of 200?" - Method 1: Using the Formula
The most straightforward way to solve this problem is using the basic percentage formula:
(Part / Whole) x 100 = Percentage
Let's plug in our values:
(32 / 200) x 100 = Percentage
This simplifies to:
0.16 x 100 = 16%
Therefore, 32 is 16% of 200.
Calculating "32 is What Percent of 200?" - Method 2: Using Proportions
Another effective method involves setting up a proportion. A proportion is an equation stating that two ratios are equal. We can represent the problem as follows:
32/200 = x/100
Where 'x' represents the percentage we need to find. To solve for 'x', we can cross-multiply:
32 x 100 = 200 x x
3200 = 200x
x = 3200 / 200
x = 16
Therefore, again, we find that 32 is 16% of 200.
Understanding the Relationship Between Fractions, Decimals, and Percentages
It's crucial to understand the interconvertibility between fractions, decimals, and percentages. They all represent the same value, just expressed differently:
- Fraction: 32/200
- Decimal: 0.16 (obtained by dividing 32 by 200)
- Percentage: 16% (obtained by multiplying the decimal by 100)
This fluidity allows you to choose the method that best suits your understanding and the complexity of the problem.
Practical Applications of Percentage Calculations
Understanding percentages is vital in many real-world scenarios:
- Finance: Calculating interest rates, loan repayments, discounts, profit margins, and investment returns.
- Retail: Determining sale prices, calculating markups, and analyzing sales data.
- Statistics: Interpreting data, representing proportions, and understanding statistical significance.
- Science: Expressing experimental results, analyzing data sets, and representing concentrations.
- Everyday life: Calculating tips, splitting bills, understanding tax rates, and comparing prices.
Common Mistakes to Avoid When Calculating Percentages
While percentage calculations are relatively straightforward, some common mistakes can lead to incorrect results:
- Incorrect Formula Application: Using the wrong formula or misplacing values can easily lead to errors. Always double-check your formula and ensure you're using the correct 'part' and 'whole'.
- Decimal Point Errors: Careless handling of decimal points during calculations can significantly affect the outcome. Pay close attention to decimal places, particularly when multiplying or dividing.
- Misunderstanding the Context: Always ensure you correctly identify the 'part' and the 'whole' in the context of the problem. Misinterpreting these values will result in an incorrect percentage.
- Using Incorrect Units: When dealing with percentages in real-world scenarios involving measurements or quantities, ensure your units are consistent and correctly applied to avoid errors.
Advanced Percentage Problems and Techniques
Beyond the basic percentage calculations, many more complex problems exist. Here are a few examples and the techniques to solve them:
- Finding the Whole: If you know the percentage and the part, you can calculate the whole using the formula: Whole = (Part / Percentage) x 100
- Finding the Part: If you know the percentage and the whole, you can calculate the part using the formula: Part = (Percentage / 100) x Whole
- Percentage Change: This involves calculating the increase or decrease in a value expressed as a percentage. The formula is: [(New Value - Old Value) / Old Value] x 100
- Compound Interest: This deals with interest earned not only on the principal but also on accumulated interest. The formula is more complex and involves exponential functions.
Mastering Percentage Calculations: Tips and Tricks
- Practice Regularly: The best way to master percentage calculations is to practice regularly. Solve various problems, starting with simple ones and gradually progressing to more complex ones.
- Use Visual Aids: Diagrams, charts, and other visual aids can help visualize the problem and understand the relationships between the different values.
- Check Your Work: Always check your work to ensure your calculations are accurate. Use alternative methods to verify your answers if possible.
- Utilize Online Resources: Several online calculators and resources are available to help you with percentage calculations. However, always understand the underlying principles to ensure you can independently solve problems.
Conclusion
Understanding how to calculate percentages is a valuable skill that has widespread applications in various aspects of life. By understanding the fundamental concepts, mastering the different methods of calculation, and avoiding common errors, you can confidently tackle percentage problems of any complexity. Remember that consistent practice and a thorough understanding of the underlying principles are key to achieving mastery in this essential mathematical skill. The seemingly simple question, "32 is what percent of 200?" opens the door to a wider understanding of percentages and their practical applications in everyday life and beyond.
Latest Posts
Latest Posts
-
What Is Equivalent To 4 9
May 10, 2025
-
300 Sq Yard To Sq Ft
May 10, 2025
-
What Is 6 2 In Expanded Form
May 10, 2025
-
What Is The Greatest Common Factor Of 42 And 54
May 10, 2025
-
How To Get Standard Form From Slope Intercept
May 10, 2025
Related Post
Thank you for visiting our website which covers about 32 Is What Percent Of 200 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.