32 Is What Percent Of 60
Treneri
May 11, 2025 · 5 min read
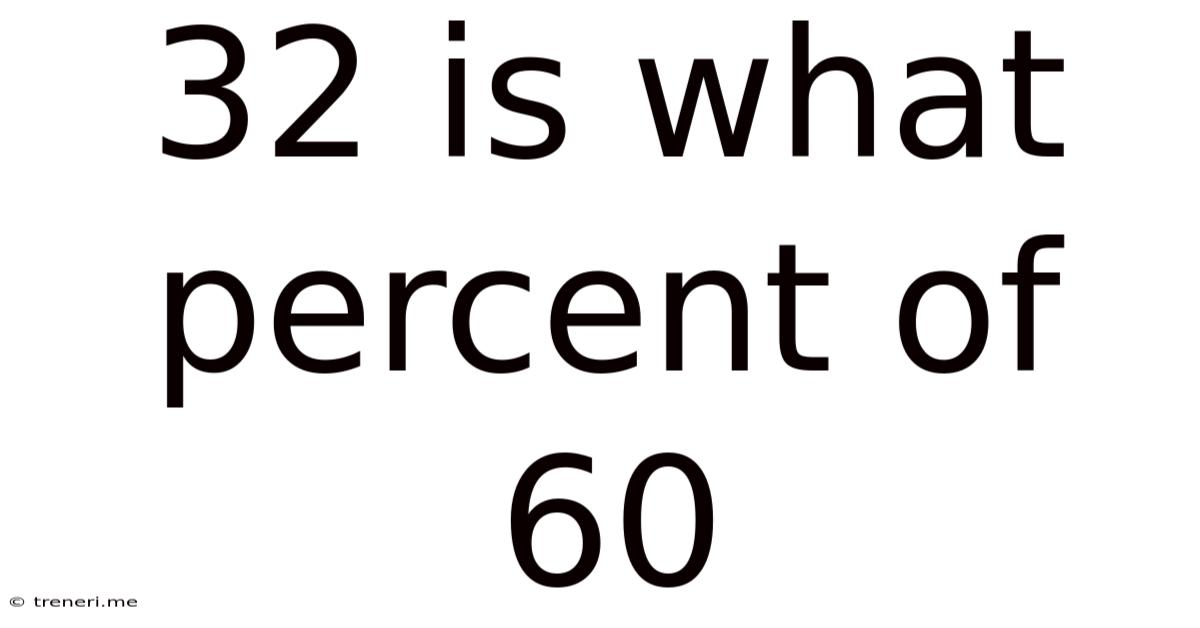
Table of Contents
32 is What Percent of 60? A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill in various aspects of life, from calculating discounts and taxes to analyzing data and interpreting statistics. This comprehensive guide will delve into the question, "32 is what percent of 60?", providing not only the answer but also a thorough explanation of the underlying methodology and its broader applications. We'll explore various methods for solving this type of problem, offering practical examples and demonstrating how these techniques can be adapted to solve similar percentage calculations.
Understanding Percentages: The Basics
Before diving into the specific calculation, let's solidify our understanding of percentages. A percentage is simply a fraction or ratio expressed as a number out of 100. The symbol "%" represents "per hundred" or "out of 100." For example, 50% means 50 out of 100, which is equivalent to 50/100 or 1/2.
Understanding this basic principle is crucial for tackling percentage problems. The key is to translate the problem into a mathematical equation that you can solve.
Method 1: Using the Percentage Formula
The most straightforward method to determine what percentage 32 represents of 60 is to use the basic percentage formula:
(Part / Whole) x 100% = Percentage
In this case:
- Part: 32 (the number we want to express as a percentage)
- Whole: 60 (the total number)
Substituting these values into the formula:
(32 / 60) x 100% = Percentage
This simplifies to:
0.5333 x 100% = 53.33%
Therefore, 32 is 53.33% of 60.
This method is highly versatile and applicable to numerous percentage problems. Simply identify the "part" and the "whole," plug them into the formula, and solve.
Method 2: Setting up a Proportion
Another effective approach is to set up a proportion. A proportion is an equation that states that two ratios are equal. We can represent the problem as:
32 / 60 = x / 100
Where 'x' represents the percentage we're trying to find. To solve for 'x', we cross-multiply:
32 x 100 = 60x
3200 = 60x
x = 3200 / 60
x = 53.33
Therefore, once again, we arrive at the answer: 32 is 53.33% of 60. This method provides a visual representation of the relationship between the parts and the whole, making it easier to understand the underlying concept.
Method 3: Using Decimal Conversion
This method involves first converting the fraction 32/60 into a decimal. We divide 32 by 60:
32 ÷ 60 = 0.5333
Then, to express this decimal as a percentage, we multiply by 100%:
0.5333 x 100% = 53.33%
This method is particularly useful when working with calculators or when you need a quick estimation. The decimal representation gives a clear understanding of the proportional relationship between 32 and 60.
Practical Applications of Percentage Calculations
Understanding how to calculate percentages is essential in many real-world situations. Here are some examples:
1. Discounts and Sales:
Imagine a store offering a 20% discount on an item priced at $60. To calculate the discount amount, we'd find 20% of $60: (20/100) x $60 = $12. The sale price would be $60 - $12 = $48. This same principle applies to various sales and discounts encountered daily.
2. Taxes:
Sales tax calculations involve percentages. If the sales tax rate is 8%, and you purchase an item for $50, the tax amount would be (8/100) x $50 = $4. Your total cost would be $50 + $4 = $54. Understanding tax calculations helps in budgeting and managing personal finances.
3. Grade Calculation:
In education, percentages are fundamental for calculating grades. If a student scores 32 points out of a possible 60 points on a test, their percentage score is calculated using the same methods described above, resulting in a score of 53.33%.
4. Data Analysis and Statistics:
Percentages are indispensable for analyzing data and interpreting statistics. For instance, in market research, understanding the percentage of consumers who prefer a specific product helps in making informed business decisions. In finance, analyzing percentage changes in investment values over time is critical for evaluating portfolio performance. Understanding these percentages is key to understanding trends and patterns.
5. Financial Calculations:
Interest rates, profit margins, and returns on investment are all expressed as percentages. Understanding these percentages is crucial for making financial decisions, whether it involves calculating loan repayments, analyzing investment opportunities, or understanding business profitability. The ability to quickly perform percentage calculations is a valuable asset in personal and business finance.
Beyond the Basics: Working with More Complex Percentages
The techniques described above are not limited to simple calculations like "32 is what percent of 60?". They can be adapted to solve more complex percentage problems:
-
Finding the whole: If you know the percentage and the part, you can calculate the whole. For example, if 25% of a number is 15, you can set up the equation: (25/100) x Whole = 15. Solving for "Whole" gives you the answer.
-
Finding the part: If you know the percentage and the whole, you can calculate the part. For example, if you need to find 10% of 200, you would calculate (10/100) x 200 = 20.
-
Percentage change: Calculating percentage change involves finding the difference between two numbers and expressing that difference as a percentage of the original number. This is frequently used to track changes in prices, population, or other data points. The formula is: [(New Value - Old Value) / Old Value] x 100%.
-
Percentage increase/decrease: These calculations determine the percentage by which a value has increased or decreased compared to a previous value. They are commonly used to track growth or decline in various areas.
Mastering these fundamental percentage calculation techniques opens a wide range of problem-solving capabilities across various disciplines.
Conclusion: Mastering Percentage Calculations for Success
The ability to calculate percentages accurately and efficiently is a valuable skill applicable across numerous fields. Understanding the basic percentage formula, along with alternative methods like proportions and decimal conversion, empowers you to confidently tackle various percentage-related problems. From everyday calculations to complex data analysis, this skill enhances your problem-solving abilities and contributes to better decision-making in various contexts. Remember to practice regularly, explore various problem types, and apply your knowledge to real-world scenarios to fully grasp the power of percentage calculations. The seemingly simple question, "32 is what percent of 60?" serves as a gateway to a world of quantitative understanding.
Latest Posts
Latest Posts
-
How Long Is 182 Days In Months
May 11, 2025
-
Cuantos Son 90 Dias En Meses
May 11, 2025
-
5 Pies 6 Pulgadas En Metros
May 11, 2025
-
Cuanto Es Menos 40 Grados Fahrenheit En Centigrados
May 11, 2025
-
How Much Is 50000 Hawaiian Miles Worth
May 11, 2025
Related Post
Thank you for visiting our website which covers about 32 Is What Percent Of 60 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.