36 Is What Percent Of 30
Treneri
May 10, 2025 · 4 min read
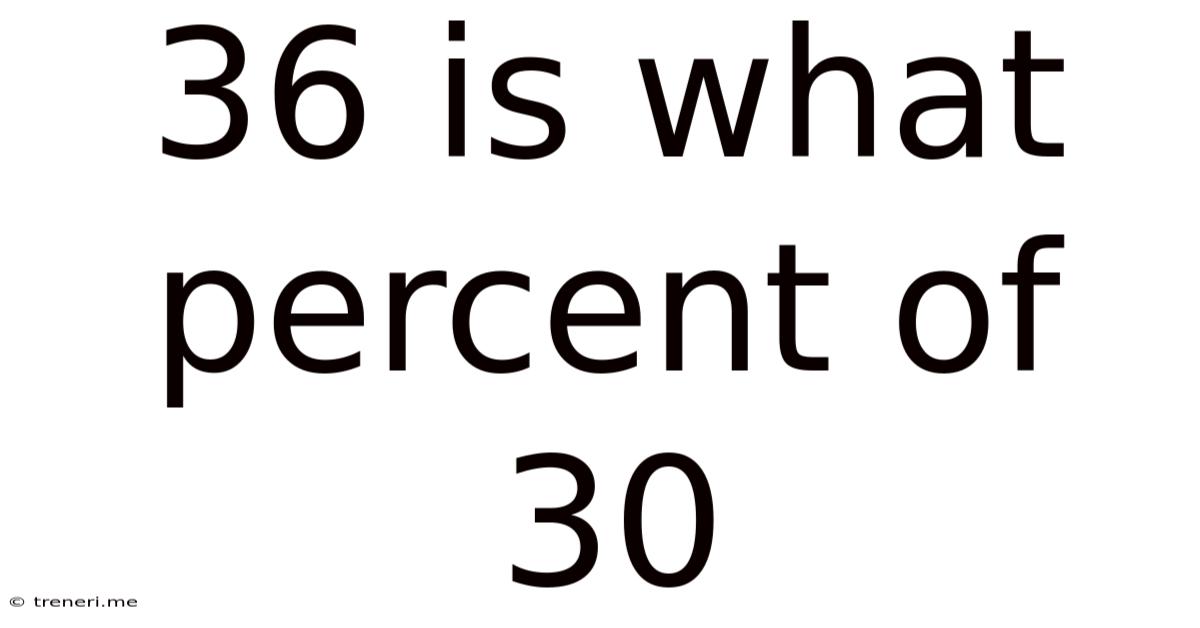
Table of Contents
36 is What Percent of 30? A Comprehensive Guide to Percentage Calculations
This seemingly simple question, "36 is what percent of 30?", opens the door to a world of percentage calculations crucial for everyday life, from understanding sales discounts to analyzing financial reports. This comprehensive guide will not only answer the question but also equip you with the knowledge and skills to tackle similar problems confidently. We'll explore different methods for solving percentage problems, delve into the underlying concepts, and provide real-world examples to solidify your understanding.
Understanding Percentages
Before diving into the calculation, let's refresh our understanding of percentages. A percentage is a fraction or a ratio expressed as a number out of 100. The symbol "%" represents "percent," meaning "out of 100" or "per hundred." For instance, 50% means 50 out of 100, which is equivalent to ½ or 0.5.
Method 1: Using the Formula
The most straightforward method to solve "36 is what percent of 30?" involves using the basic percentage formula:
(Part / Whole) x 100 = Percentage
In this case:
- Part: 36 (the number we're comparing)
- Whole: 30 (the total number)
Plugging these values into the formula:
(36 / 30) x 100 = 120%
Therefore, 36 is 120% of 30.
Method 2: Setting up a Proportion
Another effective approach is to set up a proportion. A proportion is a statement that two ratios are equal. We can represent the problem as:
36/30 = x/100
Where 'x' represents the percentage we need to find. To solve for 'x', we cross-multiply:
30x = 3600
x = 3600 / 30
x = 120
This confirms that 36 is 120% of 30.
Method 3: Using Decimal Conversion
This method involves converting the fraction to a decimal and then multiplying by 100 to express it as a percentage.
- Divide the part by the whole: 36 / 30 = 1.2
- Multiply by 100: 1.2 x 100 = 120%
Again, we arrive at the conclusion that 36 is 120% of 30.
Why is the Result Greater than 100%?
It's important to understand that a percentage greater than 100% indicates that the "part" is larger than the "whole." In this case, 36 is larger than 30. This situation is common in various contexts, such as:
- Growth and Increase: If 30 represents initial sales and 36 represents sales after an increase, the 120% signifies a 20% growth.
- Financial Analysis: When comparing current values against previous values, results exceeding 100% indicate growth or increase.
- Statistical Comparisons: In statistical analysis, percentages over 100% can appear when comparing groups or samples.
Real-World Applications: Examples
Percentage calculations are used extensively in numerous real-life scenarios. Let's explore a few examples:
1. Sales and Discounts:
A store offers a 20% discount on an item originally priced at $30. To find the discounted price:
- Calculate the discount amount: 20% of $30 = (20/100) x $30 = $6
- Subtract the discount from the original price: $30 - $6 = $24
The discounted price is $24. Conversely, if the discounted price is $24 and the original price is $30, you could calculate the percentage discount using the methods discussed earlier.
2. Financial Growth and Investment Returns:
Imagine you invested $30, and your investment grew to $36. To calculate the percentage return:
Using the formula: (36/30) x 100 = 120%
This indicates a 20% return on your investment (120% - 100% = 20%).
3. Grade Calculations:
If you scored 36 points out of a possible 30 points on a test (perhaps due to bonus points), your percentage score would be:
(36/30) x 100 = 120%
This indicates you exceeded the maximum possible points and scored 120% of the total.
4. Population Growth:
If a town's population increased from 30,000 to 36,000, the percentage increase would be:
(36000/30000) x 100 = 120%
This represents a 20% population growth.
Advanced Percentage Calculations
While the examples above focus on simple percentage calculations, more complex scenarios might involve multiple percentage changes or compound interest. These calculations require a deeper understanding of percentage operations and often involve multiple steps. However, the fundamental principles remain the same: understanding the "part" and the "whole" is crucial.
Tips for Mastering Percentage Calculations:
- Practice Regularly: Consistent practice is key to mastering any mathematical concept, including percentages.
- Understand the Concepts: Don't just memorize formulas; understand the underlying logic behind percentage calculations.
- Use Multiple Methods: Try solving problems using different methods (formula, proportion, decimal conversion) to develop a versatile approach.
- Real-World Application: Relate percentage calculations to real-life situations to improve comprehension and retention.
- Utilize Online Resources: There are numerous online resources, including calculators and tutorials, to assist you in learning and practicing.
Conclusion:
The question, "36 is what percent of 30?" serves as a springboard to explore the versatile world of percentage calculations. By understanding the different methods and applying them to real-world examples, you can confidently solve percentage problems and apply this essential skill in various aspects of your life, from managing finances to analyzing data. Remember that a percentage above 100% simply indicates that the "part" exceeds the "whole," representing growth or increase. Mastering percentage calculations empowers you to interpret data effectively and make informed decisions.
Latest Posts
Latest Posts
-
How Much Time Is 300 Seconds
May 11, 2025
-
What Is 1 Of 8 Million
May 11, 2025
-
How Many Gallons In A 15x30 Pool
May 11, 2025
-
Gcf Of 12 18 And 30
May 11, 2025
-
649 Rounded To The Nearest Hundred
May 11, 2025
Related Post
Thank you for visiting our website which covers about 36 Is What Percent Of 30 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.