4 5 12 3 2 7
Treneri
May 15, 2025 · 5 min read
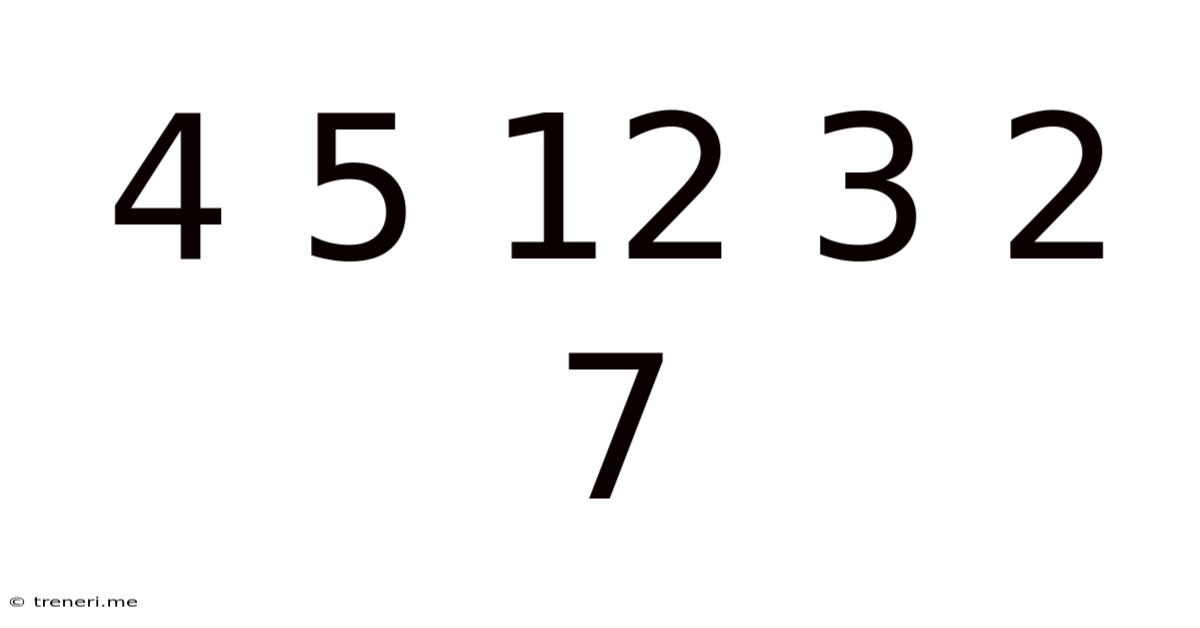
Table of Contents
Decoding the Sequence: Exploring the Mysteries of 4 5 12 3 2 7
The seemingly innocuous sequence 4 5 12 3 2 7 presents a captivating challenge. At first glance, it appears random, a jumble of numbers lacking any discernible pattern. However, the beauty of mathematics lies in its ability to reveal hidden order within apparent chaos. This article delves deep into the potential patterns, underlying structures, and possible interpretations of this intriguing numerical sequence. We'll explore various mathematical approaches, discuss potential algorithms, and consider the broader implications of such seemingly simple sequences.
Beyond the Obvious: Initial Explorations
Before diving into complex mathematical models, let's start with the basics. The immediate reaction might be to look for simple arithmetic relationships: addition, subtraction, multiplication, or division between consecutive numbers. However, a cursory examination reveals no straightforward pattern using these basic operations. The sequence jumps around erratically, frustrating any attempt at a quick, easily-identifiable solution.
- Difference Analysis: Calculating the differences between consecutive numbers yields: 1, 7, -9, -1, 5. This again reveals no clear, consistent pattern.
- Ratio Analysis: Similarly, examining the ratios between consecutive numbers produces equally inconclusive results: 1.25, 2.4, -4, -3, 3.5.
This lack of simple arithmetic consistency suggests a more nuanced approach is necessary. The seemingly random nature of the sequence hints at a deeper, possibly more abstract, mathematical structure.
The Power of Pattern Recognition: Exploring Potential Algorithms
Given the absence of readily apparent arithmetic progressions, let's consider the possibility of more sophisticated algorithms governing this sequence.
Hidden Functions and Recursion
One avenue of investigation lies in exploring recursive functions. A recursive function is one that calls itself within its own definition. This creates a chain of calculations, potentially leading to a complex pattern. Could the sequence 4 5 12 3 2 7 be generated by a recursively defined function?
A potential, though likely not unique, approach might involve a function incorporating modular arithmetic or other more complex mathematical operations. For example, a hypothetical recursive function could involve elements like:
- Previous terms: The value of a given term might depend on one or more preceding terms.
- Modular arithmetic: The sequence might use modulo operations to cycle through a limited range of values.
- Conditional statements: The next term might be determined based on specific conditions involving previous terms.
However, constructing such a function requires extensive experimentation and careful consideration of potential patterns within the data. Finding the correct function would likely involve trial and error, informed by intuition and mathematical insight.
Prime Numbers and Factorization
Another approach involves investigating the prime factorization of each number in the sequence. Prime factorization decomposes a number into its prime factors (numbers divisible only by 1 and themselves). Examining the prime factors of 4, 5, 12, 3, 2, and 7 might reveal hidden relationships or patterns.
- 4 = 2 x 2
- 5 = 5
- 12 = 2 x 2 x 3
- 3 = 3
- 2 = 2
- 7 = 7
While no immediately obvious pattern emerges from this analysis, the inclusion of prime numbers suggests a potential link to number theory. Further exploration might involve examining the distribution of prime numbers, their gaps, and other properties within the context of the sequence.
Beyond Arithmetic: Geometric and Combinatorial Interpretations
Stepping away from purely arithmetic approaches, we can explore more abstract mathematical frameworks.
Geometric Interpretations
Could the sequence represent coordinates in a multi-dimensional space? Or perhaps represent distances or angles in a geometric figure? While highly speculative, this perspective offers a fresh lens through which to view the sequence. The absence of readily apparent geometric properties suggests this interpretation is likely more complex and would require significant exploration.
Combinatorial Interpretations
Combinatorics deals with counting and arranging objects. Could this sequence be linked to permutations, combinations, or other combinatorial structures? While initially less intuitive, a deeper investigation might reveal that the numbers represent the size of sets, the number of ways to arrange objects, or other combinatorial features.
The Role of Context: Unlocking the Sequence's Meaning
The interpretation of the sequence 4 5 12 3 2 7 depends heavily on context. If this sequence were obtained from a specific mathematical problem, game, or real-world phenomenon, understanding that context is crucial to deciphering its meaning.
Without knowing its source, we are left with possibilities based purely on mathematical speculation. Its origin could significantly influence the type of analysis needed to uncover its structure and underlying pattern.
Advanced Techniques and Future Explorations
More advanced techniques could be employed to analyze this sequence, including:
- Statistical analysis: Analyzing the sequence's statistical properties, such as its mean, variance, and distribution, might reveal hidden information.
- Machine learning: Machine learning algorithms could be trained on the sequence to identify potential patterns and extrapolate future values. However, the limited amount of data makes this challenging.
- Chaos theory: The seemingly random nature of the sequence might suggest a link to chaotic systems, whose behavior, though deterministic, appears random.
Further research could explore the possibility of extending the sequence, collecting more data points if possible. Additional data might lead to clearer patterns and a more definitive understanding of the underlying structure.
Conclusion: The Ongoing Quest for Pattern
The sequence 4 5 12 3 2 7 presents a fascinating puzzle. Its lack of immediately apparent patterns requires a multifaceted approach, involving various mathematical techniques and creative thinking. While a definitive solution remains elusive without further context, the journey of exploring potential algorithms, mathematical frameworks, and advanced techniques reveals the rich complexity inherent even in a seemingly simple sequence of numbers. The mystery of 4 5 12 3 2 7 underscores the enduring allure of pattern recognition and the inexhaustible depth of mathematical inquiry. Further investigation is encouraged, potentially leading to new insights and perhaps a definitive solution to this intriguing numerical riddle.
Latest Posts
Latest Posts
-
Greatest Common Factor Of 75 And 30
May 15, 2025
-
Greatest Common Factor Of 44 And 16
May 15, 2025
-
Least Common Multiple Of 2 3 And 4
May 15, 2025
-
What Is 3 4 Of A Foot
May 15, 2025
-
Dos Metros Y Medio En Pies
May 15, 2025
Related Post
Thank you for visiting our website which covers about 4 5 12 3 2 7 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.