4/5 Divided By 2/3 As A Fraction
Treneri
May 10, 2025 · 4 min read
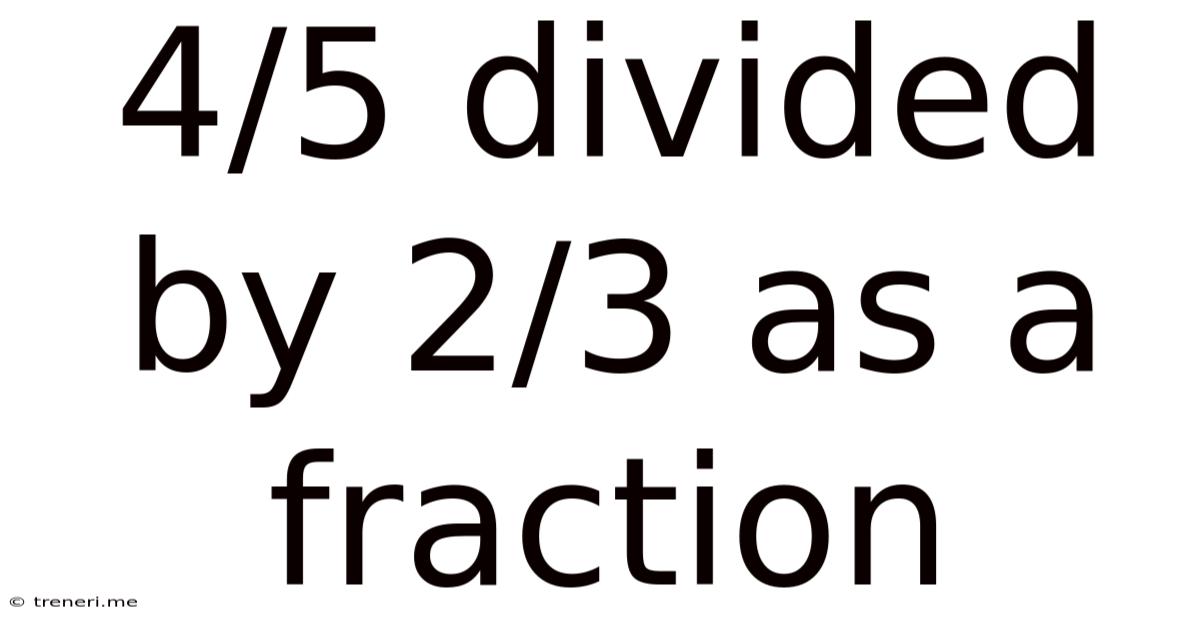
Table of Contents
4/5 Divided by 2/3 as a Fraction: A Comprehensive Guide
Dividing fractions can seem daunting at first, but with a clear understanding of the process, it becomes straightforward. This comprehensive guide will walk you through dividing 4/5 by 2/3, explaining the steps involved and providing additional examples to solidify your understanding. We'll explore different methods, address common misconceptions, and delve into the underlying mathematical principles. By the end, you'll be confident in tackling similar fraction division problems.
Understanding Fraction Division: The "Keep, Change, Flip" Method
The most common and arguably easiest method for dividing fractions is the "keep, change, flip" method (also known as the "invert and multiply" method). This method simplifies the division process by transforming it into a multiplication problem.
Here's the breakdown:
- Keep: Keep the first fraction exactly as it is. In our case, this is 4/5.
- Change: Change the division sign (÷) to a multiplication sign (×).
- Flip: Flip (or reciprocate) the second fraction. This means switching the numerator and the denominator. The reciprocal of 2/3 is 3/2.
Therefore, 4/5 ÷ 2/3 becomes 4/5 × 3/2.
Performing the Multiplication
Now that we've transformed the division problem into a multiplication problem, the process is much simpler. We multiply the numerators together and the denominators together:
(4 × 3) / (5 × 2) = 12/10
Simplifying the Fraction
The fraction 12/10 is an improper fraction (the numerator is larger than the denominator). We can simplify this fraction by finding the greatest common divisor (GCD) of the numerator and the denominator. The GCD of 12 and 10 is 2. We divide both the numerator and the denominator by 2:
12 ÷ 2 = 6 10 ÷ 2 = 5
Therefore, the simplified fraction is 6/5. This can also be expressed as a mixed number: 1 1/5.
Visualizing Fraction Division
Understanding the concept of division visually can be helpful. Imagine you have 4/5 of a pizza. You want to divide this 4/5 into portions of 2/3. How many portions do you get? This is precisely what the division problem 4/5 ÷ 2/3 is asking.
While a visual representation isn't always practical for complex fractions, it can be a valuable tool for building intuition and understanding the underlying concept.
Alternative Method: Using Common Denominators
Another method for dividing fractions involves finding a common denominator for both fractions. While this method might seem more complex initially, it provides a deeper understanding of the underlying mathematical principles.
-
Find a Common Denominator: The least common denominator (LCD) of 5 and 3 is 15.
-
Convert Fractions to Equivalent Fractions:
- 4/5 becomes 12/15 (multiply both numerator and denominator by 3)
- 2/3 becomes 10/15 (multiply both numerator and denominator by 5)
-
Rewrite the Division: The problem now becomes 12/15 ÷ 10/15.
-
Divide the Numerators: Now, because the denominators are the same, we can simply divide the numerators: 12 ÷ 10 = 1.2
-
Convert to a Fraction: 1.2 can be expressed as 6/5. This matches the result we obtained using the "keep, change, flip" method.
Addressing Common Misconceptions
Several common misconceptions can arise when dividing fractions:
-
Flipping the Wrong Fraction: Remember, you only flip (reciprocate) the second fraction (the divisor). Flipping the first fraction will lead to an incorrect answer.
-
Multiplying Instead of Dividing (or vice-versa): Clearly distinguish between multiplication and division problems. While the "keep, change, flip" method converts division to multiplication, the initial operation is division.
-
Forgetting to Simplify: Always simplify your answer to its lowest terms. This makes the answer more manageable and easier to interpret.
Practicing with Similar Problems
To further solidify your understanding, let's try a few more examples:
Example 1: 3/7 ÷ 1/2
- Keep: 3/7
- Change: ×
- Flip: 2/1
- Multiply: (3 × 2) / (7 × 1) = 6/7
Example 2: 5/8 ÷ 3/4
- Keep: 5/8
- Change: ×
- Flip: 4/3
- Multiply: (5 × 4) / (8 × 3) = 20/24
- Simplify: 5/6
Example 3: 1/6 ÷ 2/9
- Keep: 1/6
- Change: ×
- Flip: 9/2
- Multiply: (1 × 9) / (6 × 2) = 9/12
- Simplify: 3/4
Conclusion: Mastering Fraction Division
Dividing fractions, while seemingly complex at first, becomes manageable with the right approach and practice. The "keep, change, flip" method provides a simple and efficient way to convert fraction division into multiplication. Remember to always simplify your answer to its lowest terms. By practicing with different examples and understanding the underlying principles, you can confidently tackle any fraction division problem you encounter. Understanding both the "keep, change, flip" method and the common denominator method offers a versatile approach, reinforcing your understanding of fraction division and its mathematical basis. Remember that consistent practice is key to mastering this essential mathematical skill.
Latest Posts
Latest Posts
-
Find An Exponential Equation With Two Points
May 10, 2025
-
How Many Calories Is 2 Cups Of Uncooked Rice
May 10, 2025
-
What Is The Gcf Of 63 And 84
May 10, 2025
-
How Long Ago Was 2010 In Years
May 10, 2025
-
What Is Equivalent To 8 10
May 10, 2025
Related Post
Thank you for visiting our website which covers about 4/5 Divided By 2/3 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.