4 5 Divided By 3 10
Treneri
May 10, 2025 · 5 min read
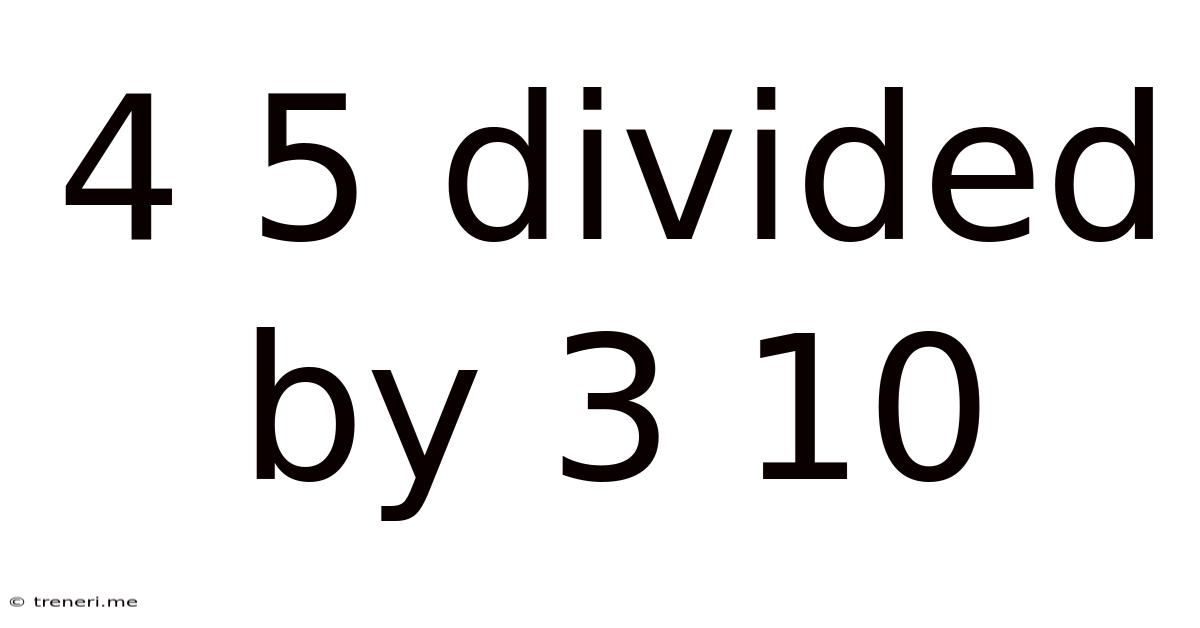
Table of Contents
Decoding the Mathematical Puzzle: 4/5 Divided by 3/10
The seemingly simple mathematical expression "4/5 divided by 3/10" can become a source of confusion for many, particularly those encountering fraction division for the first time. This comprehensive guide will not only provide the solution but also delve deep into the underlying principles, offering a thorough understanding of fraction division and its practical applications. We'll explore various methods for solving this problem, emphasizing the importance of conceptual understanding alongside procedural fluency. By the end, you'll be confident in tackling similar problems and have a firm grasp of the concepts involved.
Understanding Fraction Division: The "Invert and Multiply" Method
At its core, dividing by a fraction is equivalent to multiplying by its reciprocal. This is the foundation of the widely used "invert and multiply" method. Let's break this down:
-
Reciprocal: The reciprocal of a fraction is obtained by simply swapping the numerator (top number) and the denominator (bottom number). For example, the reciprocal of 3/10 is 10/3.
-
The Process: To divide one fraction by another, we change the division operation to multiplication by taking the reciprocal of the second fraction.
Therefore, 4/5 divided by 3/10 becomes:
4/5 * 10/3
This multiplication is significantly easier to manage than the initial division problem.
Solving the Problem: Step-by-Step Calculation
-
Rewrite the problem: We've already rewritten the division problem as a multiplication: 4/5 * 10/3
-
Simplify before multiplying: Before multiplying the numerators and denominators, look for opportunities to simplify. Notice that 10 (in the numerator) and 5 (in the denominator) share a common factor of 5. We can simplify this:
10/5 = 2
Our expression now becomes:
4/1 * 2/3
-
Multiply numerators and denominators: Now, multiply the numerators together and the denominators together separately:
(4 * 2) / (1 * 3) = 8/3
-
Express as a mixed number (optional): The answer, 8/3, is an improper fraction (the numerator is larger than the denominator). We can express this as a mixed number by dividing the numerator by the denominator:
8 ÷ 3 = 2 with a remainder of 2
Therefore, 8/3 can be expressed as 2 2/3.
Therefore, 4/5 divided by 3/10 = 8/3 = 2 2/3
Alternative Methods: Visualizing Fraction Division
While the "invert and multiply" method is efficient, visualizing fraction division can provide a deeper conceptual understanding. Let's explore a couple of visual approaches:
Method 1: Using Number Lines
Imagine a number line representing the fraction 4/5. Dividing by 3/10 essentially asks, "How many groups of 3/10 are there in 4/5?" To visualize this, you could divide the number line representing 4/5 into segments of 3/10 and count how many segments fit within the 4/5 range. While this method isn't always practical for complex fractions, it strengthens the intuitive understanding of fraction division.
Method 2: Area Models
Area models can offer a powerful visual representation. Imagine a rectangle representing a whole unit. Divide this rectangle into five equal parts and shade four parts to represent 4/5. Then, further divide the rectangle into sections representing 3/10. By carefully counting the sections, you can determine how many groups of 3/10 are contained within 4/5. This method is particularly helpful for building an intuitive understanding of the underlying concept of fraction division.
Real-World Applications of Fraction Division
Fraction division is not merely an abstract mathematical concept; it has numerous real-world applications:
-
Cooking and Baking: Scaling recipes up or down often involves fraction division. If a recipe calls for 2/3 cups of flour, and you want to make only half the recipe, you need to divide 2/3 by 2 (or multiply by 1/2).
-
Sewing and Crafting: Cutting fabric or other materials into specific fractions often involves dividing lengths or areas.
-
Construction and Engineering: Precise measurements and calculations in construction and engineering projects frequently involve fractions and their division. Determining the number of pieces of material needed for a specific length or area often requires fraction division.
-
Data Analysis and Statistics: Fraction division plays a significant role in calculating ratios, proportions, and probabilities in statistical analysis.
Expanding on the Concept: Working with More Complex Fractions
The principles discussed for solving 4/5 divided by 3/10 are applicable to any fraction division problem. Let's consider a more complex example:
(7/8) / (2/5)
-
Invert and Multiply: (7/8) * (5/2)
-
Simplify (if possible): In this case, there are no common factors to simplify before multiplication.
-
Multiply: (7 * 5) / (8 * 2) = 35/16
-
Convert to a mixed number (optional): 35 ÷ 16 = 2 with a remainder of 3. Therefore, 35/16 = 2 3/16.
Mastering Fraction Division: Tips and Tricks
-
Practice Regularly: The key to mastering any mathematical skill is consistent practice. Solve various fraction division problems to build fluency and confidence.
-
Utilize Visual Aids: Visual aids like number lines and area models can greatly aid in understanding the underlying concepts.
-
Break Down Complex Problems: For more complex problems, break them down into smaller, manageable steps.
-
Check Your Work: Always check your answers to ensure accuracy.
Conclusion: Beyond the Algorithm
While the "invert and multiply" method provides an efficient algorithm for solving fraction division problems, a deep understanding of the underlying concepts is crucial. Visualizing fraction division using number lines or area models, and exploring real-world applications, will solidify your understanding and enhance your problem-solving abilities. By consistently practicing and applying these principles, you'll be well-equipped to tackle any fraction division challenge with confidence. Remember, mathematics is not just about memorizing formulas but also about grasping the underlying logic and applying it creatively to solve problems.
Latest Posts
Latest Posts
-
Formula For Perimeter Of A Pentagon
May 10, 2025
-
How Many Meters Is 2 5 Miles
May 10, 2025
-
60 Days From July 7 2024
May 10, 2025
-
26 Ounces Is How Many Cups
May 10, 2025
-
What Is The Highest Common Factor Of 72 And 27
May 10, 2025
Related Post
Thank you for visiting our website which covers about 4 5 Divided By 3 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.