4/5 Divided By 3/5 As A Fraction
Treneri
May 12, 2025 · 5 min read
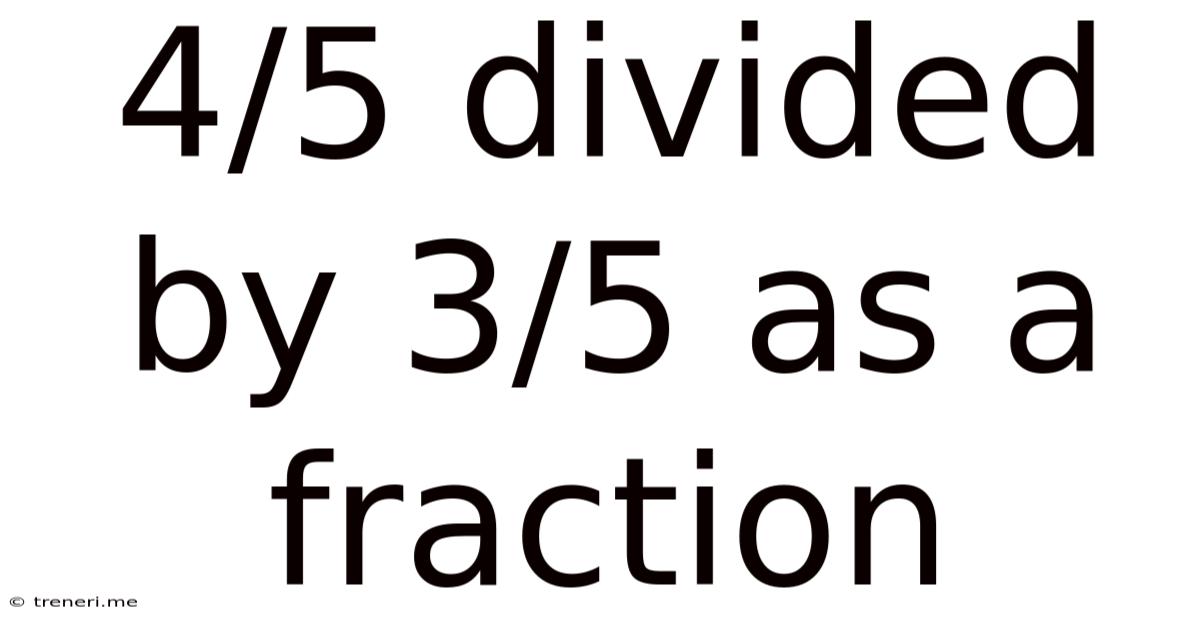
Table of Contents
4/5 Divided by 3/5 as a Fraction: A Comprehensive Guide
Dividing fractions can seem daunting, but with a clear understanding of the process, it becomes straightforward. This comprehensive guide will walk you through dividing 4/5 by 3/5, explaining the steps involved and providing additional examples to solidify your understanding. We’ll explore the concept, demonstrate the solution, and offer practical applications to make this mathematical operation clear and intuitive.
Understanding Fraction Division
Before diving into the specific problem of 4/5 divided by 3/5, let's review the fundamental principles of fraction division. The core concept revolves around the idea of reciprocals or multiplicative inverses. The reciprocal of a fraction is simply the fraction flipped upside down. For instance, the reciprocal of 3/5 is 5/3.
The crucial rule to remember is: Dividing by a fraction is the same as multiplying by its reciprocal.
This simple yet powerful rule transforms a division problem into a multiplication problem, making it significantly easier to solve.
Solving 4/5 Divided by 3/5
Now, let's tackle the problem at hand: 4/5 ÷ 3/5.
Following the rule we just established, we'll change the division problem into a multiplication problem by finding the reciprocal of 3/5 and multiplying:
4/5 ÷ 3/5 = 4/5 * 5/3
Now, we multiply the numerators (the top numbers) together and the denominators (the bottom numbers) together:
(4 * 5) / (5 * 3) = 20/15
This fraction, 20/15, can be simplified by finding the greatest common divisor (GCD) of the numerator and the denominator. The GCD of 20 and 15 is 5. Dividing both the numerator and the denominator by 5, we get:
20/15 = (20 ÷ 5) / (15 ÷ 5) = 4/3
Therefore, 4/5 divided by 3/5 equals 4/3 or 1 1/3.
Step-by-Step Breakdown
To reinforce the process, let's break down the solution into distinct steps:
-
Identify the dividend and the divisor: In the problem 4/5 ÷ 3/5, 4/5 is the dividend (the number being divided) and 3/5 is the divisor (the number by which we're dividing).
-
Find the reciprocal of the divisor: The reciprocal of 3/5 is 5/3.
-
Change the division problem to a multiplication problem: Replace the division sign (÷) with a multiplication sign (×) and use the reciprocal of the divisor. This gives us 4/5 × 5/3.
-
Multiply the numerators: Multiply the numerators together: 4 × 5 = 20.
-
Multiply the denominators: Multiply the denominators together: 5 × 3 = 15.
-
Simplify the resulting fraction: The resulting fraction is 20/15. Simplify this by dividing both the numerator and denominator by their greatest common divisor (5), resulting in 4/3.
-
Convert to a mixed number (optional): The improper fraction 4/3 can be converted to a mixed number by dividing the numerator (4) by the denominator (3). This gives us 1 with a remainder of 1, which is written as 1 1/3.
Visual Representation
Visualizing fraction division can enhance understanding. Imagine you have 4/5 of a pizza, and you want to divide it into portions of 3/5 each. How many 3/5 portions can you get? The answer, as we've calculated, is 1 1/3 portions. This means you can get one full 3/5 portion and a little more than half of another.
Practical Applications
Understanding fraction division is crucial in numerous real-world scenarios:
-
Cooking: If a recipe calls for 4/5 of a cup of flour and you want to make 3/5 of the recipe, you'll need to calculate (4/5) ÷ (3/5) to determine the amount of flour needed.
-
Sewing: If you need to cut a piece of fabric that is 4/5 of a yard long into pieces that are 3/5 of a yard each, you’ll use fraction division to determine how many pieces you can cut.
-
Construction: Calculating the amount of materials needed for a project often involves fractions and division.
-
Data Analysis: Many data analysis tasks involve working with fractions and proportions, requiring a strong understanding of fraction division.
Further Examples
Let's practice with a few more examples to solidify your understanding:
-
2/7 ÷ 1/7: The reciprocal of 1/7 is 7/1. So, 2/7 × 7/1 = 14/7 = 2.
-
3/8 ÷ 5/8: The reciprocal of 5/8 is 8/5. So, 3/8 × 8/5 = 24/40 = 3/5.
-
5/6 ÷ 2/3: The reciprocal of 2/3 is 3/2. So, 5/6 × 3/2 = 15/12 = 5/4 = 1 1/4.
Common Mistakes to Avoid
-
Forgetting to use the reciprocal: This is the most common mistake. Remember, you must find the reciprocal of the divisor and then multiply.
-
Incorrectly multiplying or simplifying fractions: Double-check your multiplication and simplification steps to avoid errors.
-
Not simplifying the final answer: Always simplify your answer to its lowest terms.
Conclusion
Dividing fractions, while initially seeming complex, is a straightforward process once you grasp the core concept of using reciprocals. By converting division problems into multiplication problems, you can easily solve even seemingly complicated fractions. Remember the steps outlined in this guide, practice with various examples, and soon you'll be confidently tackling fraction division in any context. The ability to perform fraction division is a valuable skill with widespread applications in various aspects of life, both academic and practical. Mastering this skill will undoubtedly enhance your mathematical abilities and problem-solving skills.
Latest Posts
Latest Posts
-
2 Grams Of Yeast To Teaspoons
May 14, 2025
-
Multiples That Are Shared By Two Or More Numbers
May 14, 2025
-
Cable Size For 100 Amp Service
May 14, 2025
-
What Is 40 Off Of 75
May 14, 2025
-
How Long Is 183 Days In Months
May 14, 2025
Related Post
Thank you for visiting our website which covers about 4/5 Divided By 3/5 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.