4 Divided By The Sum Of H And 7
Treneri
May 10, 2025 · 5 min read
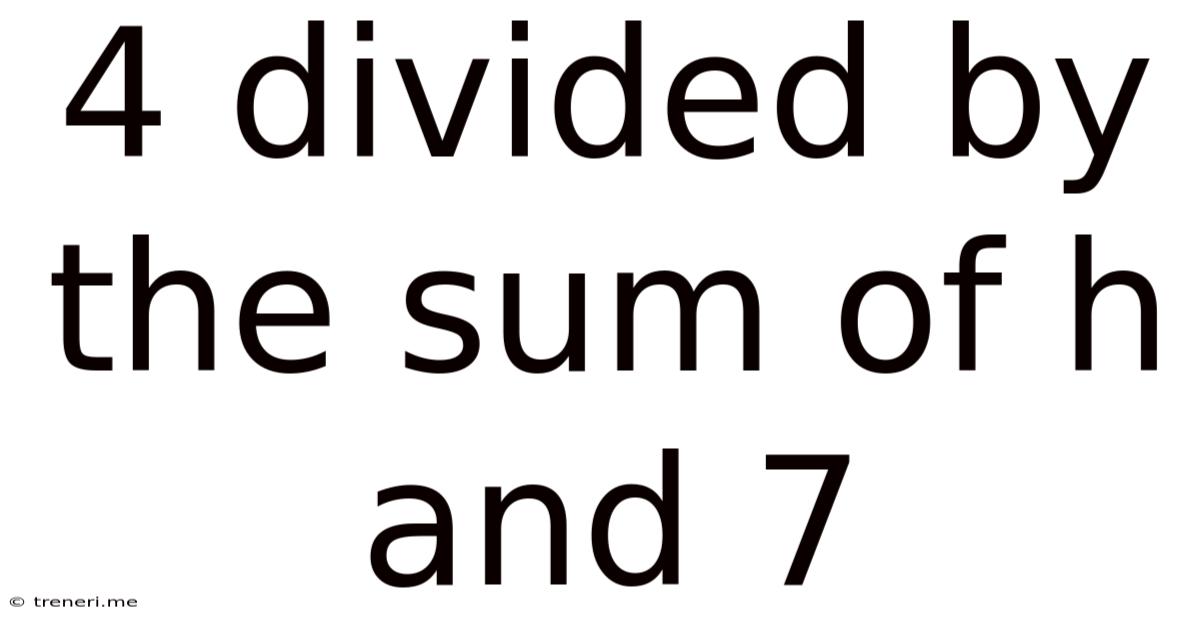
Table of Contents
4 Divided by the Sum of h and 7: A Deep Dive into Mathematical Expressions
The seemingly simple expression "4 divided by the sum of h and 7" opens up a world of mathematical exploration. This article will delve into the intricacies of this expression, exploring its various interpretations, applications, and potential extensions. We'll cover its representation in different mathematical notations, its use in solving problems, and how it relates to broader mathematical concepts. Understanding this seemingly basic expression is key to mastering more complex algebraic manipulations.
Understanding the Expression: Breaking it Down
The core of the expression lies in understanding the order of operations (often remembered by the acronym PEMDAS/BODMAS). This dictates the sequence in which mathematical operations should be performed: Parentheses/Brackets, Exponents/Orders, Multiplication and Division (from left to right), and Addition and Subtraction (from left to right).
In our case, "4 divided by the sum of h and 7" translates directly to the following mathematical expression:
4 / (h + 7)
The parentheses are crucial here. They ensure that the addition of 'h' and 7 is performed before the division by 4. Without the parentheses, the expression would be interpreted differently, leading to an incorrect result. Let's illustrate the difference:
- Correct Interpretation: 4 / (h + 7) This means we add h and 7 first, then divide the result by 4.
- Incorrect Interpretation: 4 / h + 7 This means we divide 4 by h first, and then add 7. This yields a completely different result.
This highlights the importance of precise mathematical notation and understanding the order of operations.
Evaluating the Expression for Different Values of h
The expression's value depends entirely on the value assigned to the variable 'h'. Let's explore a few examples:
Example 1: h = 3
Substituting h = 3 into the expression gives:
4 / (3 + 7) = 4 / 10 = 0.4
Example 2: h = -7
Substituting h = -7 gives:
4 / (-7 + 7) = 4 / 0
This leads to an undefined result. Division by zero is undefined in mathematics, highlighting a critical limitation of the expression. The expression is undefined when h = -7.
Example 3: h = 10
Substituting h = 10 gives:
4 / (10 + 7) = 4 / 17 ≈ 0.235
These examples demonstrate how the value of the expression changes dramatically with different inputs for 'h'. This variability is characteristic of mathematical functions and expressions.
Representing the Expression Graphically
The expression 4 / (h + 7) can be visualized as a graph, plotting the value of the expression against different values of 'h'. This graphical representation provides a clear visual understanding of the expression's behavior. The graph will exhibit a hyperbolic shape, approaching infinity as 'h' approaches -7 and approaching zero as 'h' approaches positive or negative infinity. It's a reciprocal function, showcasing a clear asymptote at h = -7.
The graph serves as a powerful tool for analyzing the expression's behavior and understanding its limitations. The asymptote at h = -7 visually confirms the undefined nature of the expression when h = -7.
Applications of the Expression
While seemingly simple, this expression has potential applications in various fields:
Physics and Engineering
This type of expression might appear in formulas related to:
- Resistance in parallel circuits: In electrical engineering, the reciprocal of total resistance in a parallel circuit involves similar additive terms in the denominator.
- Lens equations: Optics formulas often involve reciprocal relationships, which can be represented with similar fraction structures.
- Modeling rates of change: In certain physics problems involving rates of change (like velocity or acceleration), such expressions might represent a rate normalized by a sum of factors.
Economics and Finance
Although less direct, related expressions could model scenarios involving:
- Investment returns adjusted for fees: The "7" could represent a fixed management fee, and 'h' could represent variable returns, with the final expression giving a net return after fees.
Computer Science
The expression forms the basis for various algorithms, specifically in:
- Normalizing data: The expression could act as a normalization factor to scale data within a specific range.
- Weighting factors: The expression could be part of a formula that assigns weights to different factors in a calculation.
Expanding and Extending the Expression
We can modify the expression in several ways to explore its potential complexities:
- Adding a constant: We could add a constant to the expression, such as: 4 / (h + 7) + 2. This shifts the entire graph vertically.
- Multiplying by a constant: Multiplying the entire expression by a constant changes its scale but retains the basic shape. For instance, 2 * [4 / (h + 7)].
- Introducing a second variable: We could introduce another variable, for example, 4 / (h + 7 + k), adding another layer of complexity to the expression and its behavior. This addition changes the location of the asymptote.
Conclusion: The Power of Simplicity
The expression "4 divided by the sum of h and 7," while seemingly elementary, embodies fundamental principles of algebra, highlighting the crucial role of order of operations and the impact of variable values on the outcome. Its graphical representation, potential applications across diverse fields, and opportunities for expansion make it more than just a simple calculation. It serves as a building block for more complex mathematical concepts and techniques, emphasizing the power and versatility of even seemingly basic mathematical expressions. Mastering this seemingly simple expression is a vital step in developing a robust mathematical foundation. By understanding its nuances, we unlock a deeper comprehension of the principles governing mathematical relationships. This understanding extends beyond simple arithmetic, forming the basis for problem-solving across diverse domains.
Latest Posts
Latest Posts
-
Gcf Of 75 8 And 21
May 10, 2025
-
How Much Is 160ml In Cups
May 10, 2025
-
Cuanto Es 10 Yardas En Pies
May 10, 2025
-
What Is A Good Keystroke Per Hour
May 10, 2025
-
How To Change Wavelength To Frequency
May 10, 2025
Related Post
Thank you for visiting our website which covers about 4 Divided By The Sum Of H And 7 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.