4 Is 20 Percent Of What Number
Treneri
May 09, 2025 · 5 min read
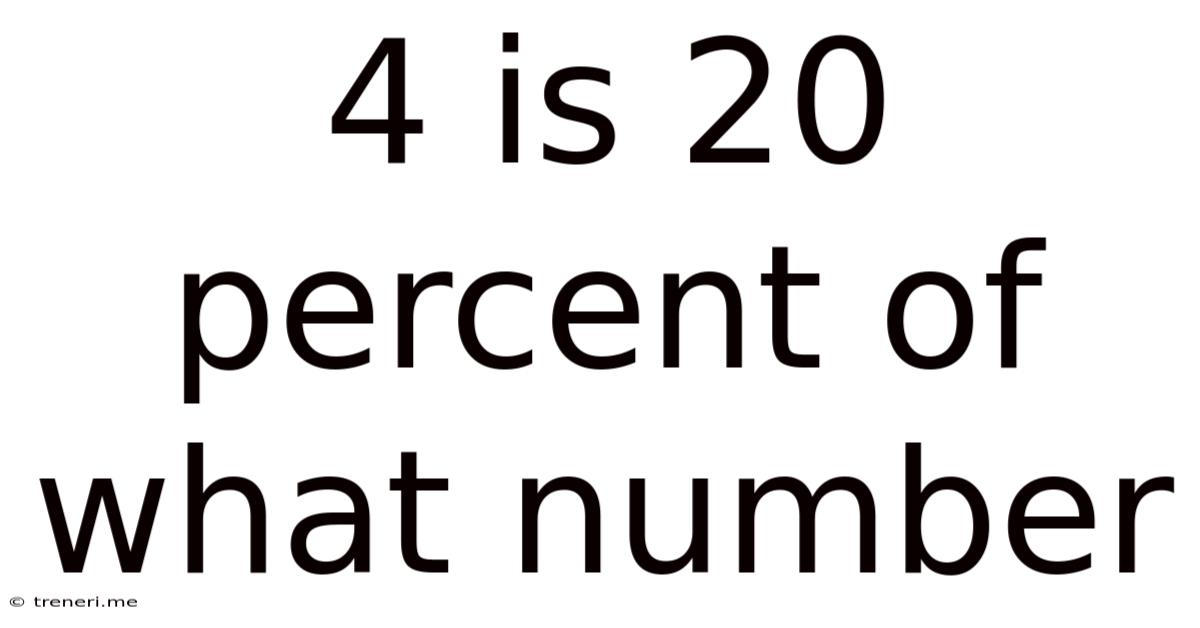
Table of Contents
4 is 20 Percent of What Number: A Comprehensive Guide to Percentage Calculations
Solving percentage problems is a fundamental skill applicable across various fields, from everyday budgeting to complex financial analyses. Understanding how to determine the whole number when given a percentage and its corresponding part is crucial. This article delves into the question, "4 is 20 percent of what number?" providing a comprehensive explanation, multiple methods of solving the problem, and practical applications to solidify your understanding.
Understanding the Problem
The question, "4 is 20 percent of what number?" presents a classic percentage problem. We're given a part (4) and a percentage (20%), and our goal is to find the whole number. This type of problem frequently arises in various scenarios:
- Sales and Discounts: Calculating the original price of an item after a discount.
- Financial Analysis: Determining total investment value based on a percentage return.
- Data Interpretation: Finding the total population based on a percentage of a subgroup.
- Scientific Measurements: Calculating the total quantity based on a percentage sample.
Method 1: Using the Percentage Formula
The most straightforward approach involves using the basic percentage formula:
Part = Percentage × Whole
In our problem:
- Part = 4
- Percentage = 20% = 0.20 (Remember to convert the percentage to a decimal by dividing by 100)
- Whole = This is what we need to find (let's represent it with 'x')
Substituting these values into the formula:
4 = 0.20 × x
To solve for 'x', we need to isolate it. We can do this by dividing both sides of the equation by 0.20:
x = 4 / 0.20
x = 20
Therefore, 4 is 20 percent of 20.
Method 2: Using Proportions
Another effective method uses proportions. We can set up a proportion relating the part to the whole and the percentage to 100%:
4/x = 20/100
To solve this proportion, we can cross-multiply:
4 × 100 = 20 × x
400 = 20x
Now, divide both sides by 20:
x = 400 / 20
x = 20
Again, we find that 4 is 20 percent of 20.
Method 3: Working Backwards from the Percentage
This method is particularly intuitive for simple percentages. If 4 represents 20%, we can find the value of 1% by dividing 4 by 20:
4 / 20 = 0.2
Since 1% is 0.2, we can find the whole (100%) by multiplying 0.2 by 100:
0.2 × 100 = 20
Thus, 4 is 20 percent of 20.
Practical Applications and Real-World Examples
Let's explore how this type of percentage calculation applies to real-world scenarios:
Scenario 1: Sales Discount
A store offers a 20% discount on a shirt, and the discount amount is $4. What was the original price of the shirt?
Using the methods described above, we find that the original price was $20.
Scenario 2: Investment Returns
An investment yields a 20% return, and the return amount is $400. What was the initial investment amount?
Applying the same principles, we determine that the initial investment was $2000.
Scenario 3: Survey Results
A survey shows that 20% of respondents prefer a particular brand, and this represents 400 people. How many people participated in the survey?
Using our percentage calculation, we find that 2000 people participated in the survey.
Scenario 4: Grade Calculation
A student scores 4 points out of a possible 20 points on a quiz. What percentage did the student score?
This is a slightly different application, but it showcases the versatility of percentage calculations. In this case, you would calculate the percentage as (4/20) * 100% = 20%
Scenario 5: Ingredient Ratios
A recipe calls for 4 grams of salt, which represents 20% of the total dry ingredients. What is the total weight of the dry ingredients?
Again, the same calculation applies, yielding a total dry ingredient weight of 20 grams.
Beyond the Basics: Dealing with More Complex Percentages
While the examples above utilize a straightforward 20% scenario, the same principles apply to more complex percentages. For instance, if the question was "4 is 3.5% of what number?", the method would remain consistent:
- Convert the percentage to a decimal: 3.5% = 0.035
- Apply the formula: 4 = 0.035x
- Solve for x: x = 4 / 0.035 ≈ 114.29
This demonstrates that the fundamental understanding of percentage calculations can easily be extended to handle more intricate problems. Practice with various percentages and values will build proficiency and confidence.
Tips for Mastering Percentage Calculations
- Practice Regularly: Consistent practice is key to mastering any mathematical skill. Work through various problems with different percentage values and parts.
- Use Multiple Methods: Experiment with different approaches (formula, proportion, working backward) to find the method that resonates best with your learning style.
- Check Your Work: Always verify your solution using a different method to ensure accuracy.
- Understand the Context: When applying percentages to real-world problems, carefully consider the context and ensure your answer is logically sound.
- Utilize Online Resources: Numerous online calculators and tutorials can assist in practicing and reinforcing your understanding.
Conclusion
The question, "4 is 20 percent of what number?" provides a valuable introduction to the fundamental principles of percentage calculations. By understanding the underlying concepts and applying various methods, you can confidently solve a wide range of percentage problems. This skill is not only valuable for academic pursuits but also essential for navigating numerous real-world situations requiring accurate and efficient percentage computations. Remember to practice regularly and apply your knowledge to diverse scenarios to reinforce your understanding and build confidence in tackling more complex percentage problems in the future.
Latest Posts
Latest Posts
-
Is Uv 3 Good For Tanning
May 10, 2025
-
Cuanto Es 1000 Pies En Metros
May 10, 2025
-
Greatest Common Factor Of 3 And 18
May 10, 2025
-
1 Psi To Inches Of Water Column
May 10, 2025
-
What Is 20 Percent Of 400 000
May 10, 2025
Related Post
Thank you for visiting our website which covers about 4 Is 20 Percent Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.