4 Is 5 Of What Number
Treneri
May 13, 2025 · 5 min read
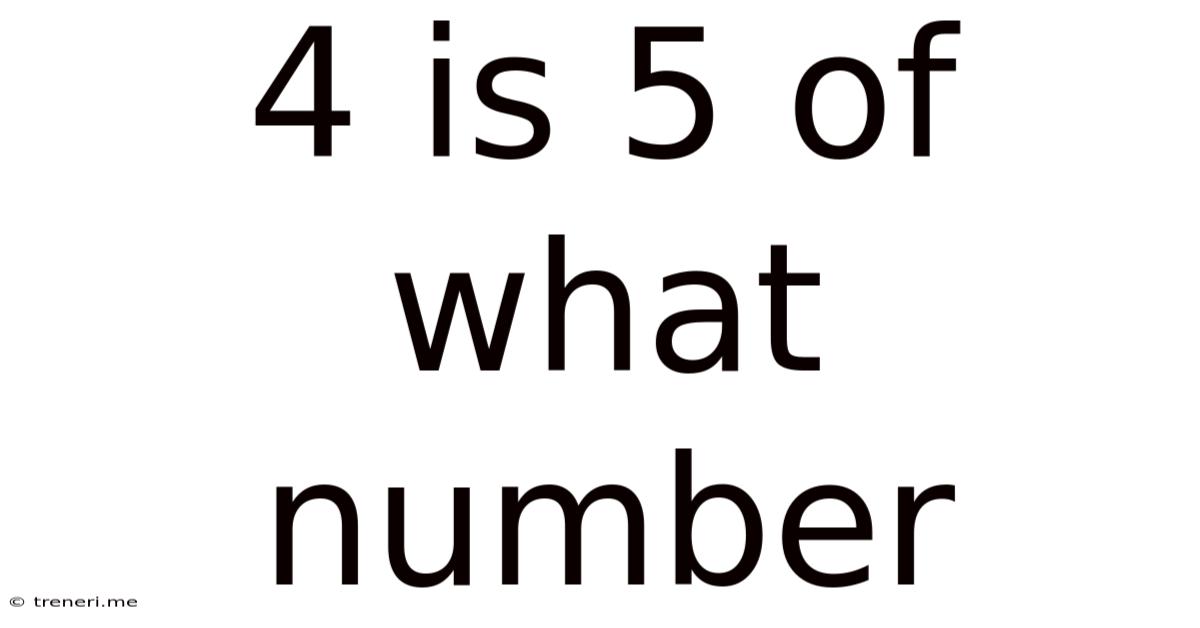
Table of Contents
4 is 5% of What Number? Unraveling the Math Behind Percentages
Percentages are a fundamental part of everyday life, cropping up in everything from sales tax calculations to understanding financial reports. One common type of percentage problem involves finding the whole number when you know a percentage of it. This article delves into the solution to the question: "4 is 5% of what number?" We'll not only solve this specific problem but also explore the underlying mathematical principles, providing you with the tools to tackle similar percentage problems with confidence.
Understanding Percentages: A Foundation
Before we jump into the solution, let's solidify our understanding of percentages. A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per hundred." For example, 25% means 25 out of 100, which can be written as the fraction 25/100 or the decimal 0.25.
Understanding this basic relationship is key to solving percentage problems. We often use percentages to represent proportions or ratios. For instance, if you score 80% on a test, it means you answered 80 out of every 100 questions correctly.
Solving "4 is 5% of What Number?"
Now, let's tackle the specific problem: "4 is 5% of what number?" This is a classic percentage problem that requires us to find the original whole number. We can approach this using a few different methods:
Method 1: Using the Percentage Formula
The most straightforward method involves using the standard percentage formula:
Part = Percentage × Whole
In our problem:
- Part = 4 (This is the known portion of the whole)
- Percentage = 5% = 0.05 (Remember to convert the percentage to a decimal by dividing by 100)
- Whole = x (This is the unknown number we need to find)
Substituting these values into the formula, we get:
4 = 0.05 × x
To solve for x, we divide both sides of the equation by 0.05:
x = 4 / 0.05
x = 80
Therefore, 4 is 5% of 80.
Method 2: Using Proportions
Another way to approach this problem is by setting up a proportion. A proportion is a statement that two ratios are equal. We can set up a proportion relating the part to the whole:
4/x = 5/100
This proportion states that the ratio of 4 to the unknown number (x) is equal to the ratio of 5 to 100 (which represents 5%). To solve this proportion, we can cross-multiply:
4 × 100 = 5 × x
400 = 5x
Divide both sides by 5:
x = 400 / 5
x = 80
Again, we find that 4 is 5% of 80.
Method 3: Working Backwards from the Percentage
This method focuses on understanding the relationship between the part and the whole. If 4 represents 5% of a number, we can reason that 1% of that number would be 4 divided by 5:
1% = 4 / 5 = 0.8
Since 1% is 0.8, then 100% (the whole number) would be 100 times 0.8:
100% = 0.8 × 100 = 80
This confirms that 4 is 5% of 80.
Practical Applications of Percentage Problems
Understanding how to solve percentage problems like "4 is 5% of what number?" has numerous practical applications in various aspects of life:
Finance and Budgeting
- Calculating original prices: If an item is on sale for $4, representing a 5% discount, you can use this method to find the original price.
- Determining interest rates: If you've earned $4 in interest, and the interest rate is 5%, you can determine the principal amount.
- Analyzing financial statements: Percentage calculations are crucial for understanding profit margins, revenue growth, and expense ratios.
Everyday Life
- Calculating tips: If you want to leave a 5% tip on a $4 discount, you can use the same methods.
- Understanding sales tax: If the sales tax on an item is $4, representing 5% of the price, this helps you find the original price.
- Interpreting survey results: If 5% of respondents (4 people) answered a question a certain way, you can calculate the total number of respondents.
Expanding Your Percentage Problem-Solving Skills
While we've focused on "4 is 5% of what number?", the principles discussed here are applicable to a wide range of percentage problems. To further enhance your skills, consider exploring these related concepts:
- Finding the percentage: Calculate what percentage one number represents of another. For example, "What percentage of 80 is 4?"
- Finding the part: Determine the value of a percentage of a given number. For example, "What is 5% of 80?"
- Solving complex percentage problems: Tackle problems involving multiple percentages, percentage increases/decreases, and compound interest.
Mastering percentage calculations empowers you to make informed decisions in various aspects of your daily life, from personal finance to professional endeavors. By practicing different approaches and applying these techniques to real-world scenarios, you will develop a strong intuitive understanding of percentages and improve your ability to solve complex numerical problems efficiently.
Troubleshooting Common Mistakes
While solving percentage problems might seem straightforward, some common mistakes can lead to incorrect answers. Let's address some of them:
- Incorrect decimal conversion: Remember to convert percentages to decimals (e.g., 5% = 0.05) before performing calculations. Failing to do this is a frequent source of error.
- Mixing up the part and the whole: Carefully identify which value represents the part and which represents the whole in the problem statement. Confusing these two will lead to an incorrect answer.
- Calculation errors: Always double-check your calculations, particularly when dealing with decimals and division. Use a calculator if necessary to ensure accuracy.
By paying attention to these details and practicing regularly, you can avoid common mistakes and increase your accuracy in solving percentage problems.
Conclusion: Mastering Percentages for a Brighter Future
The ability to confidently solve percentage problems is a valuable skill with numerous practical applications. The question "4 is 5% of what number?" is a perfect example of a problem that showcases the fundamental principles of percentage calculations. By understanding the different methods for solving these problems – from using the formula to employing proportions – you equip yourself with the tools to tackle various percentage-related challenges effectively. Remember to practice regularly, understand the underlying concepts, and watch out for common mistakes. With consistent practice and careful attention to detail, you'll master percentages and unlock their power in your personal and professional endeavors.
Latest Posts
Latest Posts
-
6 Cups Equal How Many Quarts
May 13, 2025
-
1 Lb Peanut Butter Equal Many Cups
May 13, 2025
-
Cuanto Equivale 5 Libras En Kilos
May 13, 2025
-
What Is A 8 9 Grade Percentage
May 13, 2025
-
Best Uv Index To Tan Outside
May 13, 2025
Related Post
Thank you for visiting our website which covers about 4 Is 5 Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.