4 Is What Percent Of 15
Treneri
May 09, 2025 · 5 min read
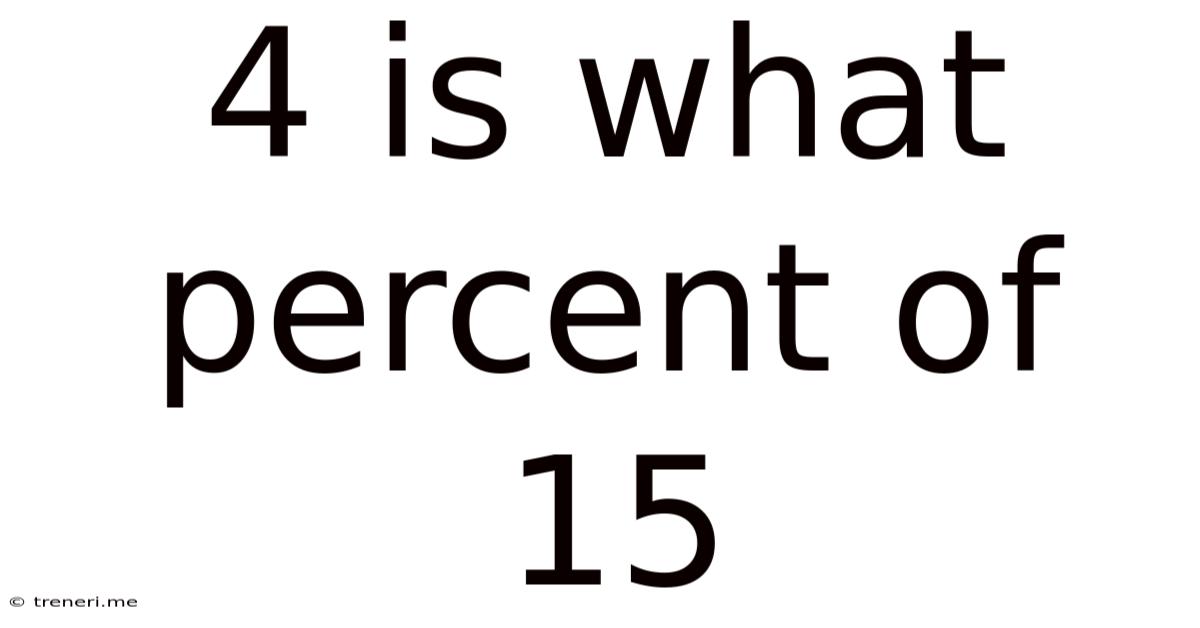
Table of Contents
4 is What Percent of 15? A Comprehensive Guide to Percentage Calculations
Calculating percentages is a fundamental skill with widespread applications in various aspects of life, from everyday budgeting and shopping to complex financial analyses and scientific research. Understanding how to determine what percentage one number represents of another is crucial for making informed decisions and interpreting data accurately. This comprehensive guide will not only answer the question "4 is what percent of 15?" but also equip you with the knowledge and tools to solve similar percentage problems with confidence.
Understanding Percentages
Before diving into the specific calculation, let's solidify our understanding of percentages. A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" signifies "percent," meaning "per hundred." For instance, 50% means 50 out of 100, or 50/100, which simplifies to 1/2 or 0.5.
Method 1: Using the Percentage Formula
The most straightforward method to determine what percentage 4 represents of 15 is to use the basic percentage formula:
(Part / Whole) x 100% = Percentage
In this case:
- Part: 4 (the number we want to express as a percentage)
- Whole: 15 (the total number)
Substituting these values into the formula:
(4 / 15) x 100% = 26.67% (approximately)
Therefore, 4 is approximately 26.67% of 15.
Method 2: Converting to a Decimal
Another approach involves converting the fraction to a decimal and then multiplying by 100%.
- Form the fraction: 4/15
- Convert to a decimal: Divide 4 by 15. This gives us approximately 0.2667.
- Multiply by 100%: 0.2667 x 100% = 26.67%
This method confirms our previous result: 4 is approximately 26.67% of 15.
Method 3: Using Proportions
Proportions offer a powerful and versatile method for solving percentage problems. We can set up a proportion to solve "4 is what percent of 15?" as follows:
4/15 = x/100
Where 'x' represents the unknown percentage. To solve for x, we cross-multiply:
4 x 100 = 15x
400 = 15x
x = 400/15
x ≈ 26.67
Again, we arrive at the same answer: 4 is approximately 26.67% of 15.
Rounding and Precision
Notice that in all our calculations, we obtained an approximate answer of 26.67%. This is due to the fact that the result (4/15) is a repeating decimal. The level of precision required depends on the context of the problem. For many applications, rounding to two decimal places (26.67%) is sufficient. However, for situations demanding higher accuracy, you can retain more decimal places or express the answer as a fraction (4/15).
Practical Applications and Real-World Examples
Understanding percentage calculations is essential for navigating numerous real-world scenarios. Here are a few examples:
1. Sales and Discounts:
Imagine a store offers a discount of $4 on an item originally priced at $15. To determine the percentage discount, you'd use the same formula: ($4/$15) x 100% ≈ 26.67%. The store is offering a 26.67% discount.
2. Grade Calculation:
If a student answered 4 out of 15 questions correctly on a test, their score would be (4/15) x 100% ≈ 26.67%. Their test score is approximately 26.67%.
3. Financial Analysis:
In finance, calculating percentages is crucial for analyzing investment returns, profit margins, and expense ratios. For example, if an investment yielded a profit of $4 on an initial investment of $15, the return on investment (ROI) would be approximately 26.67%.
4. Data Interpretation:
Percentages are widely used to represent data in charts, graphs, and reports, making it easier to visualize and understand proportions and trends. For example, if a survey shows that 4 out of 15 respondents prefer a particular product, 26.67% of respondents prefer that product.
Advanced Percentage Calculations
While the basic percentage formula covers many situations, more complex problems might require multiple steps or the application of other mathematical concepts. These scenarios often involve:
- Calculating percentage increase or decrease: This involves finding the percentage change between two values.
- Finding the original value after a percentage change: This requires working backward from the final value and the percentage change.
- Solving problems involving multiple percentages: These problems may involve applying several percentage changes successively.
Mastering Percentage Calculations: Tips and Tricks
To enhance your proficiency in calculating percentages, consider these tips:
- Practice regularly: Consistent practice is key to mastering any mathematical concept.
- Use different methods: Familiarize yourself with various methods (formula, decimal conversion, proportions) to solve percentage problems. This will allow you to choose the most efficient approach depending on the problem's complexity.
- Understand the context: Carefully analyze the problem's wording to ensure you correctly identify the "part" and the "whole."
- Check your work: Always double-check your calculations to avoid errors.
- Use calculators and online tools: Utilize calculators or online percentage calculators, especially for more complex calculations, to save time and improve accuracy. However, it's crucial to understand the underlying principles to avoid solely relying on technology.
Conclusion
Calculating percentages is a valuable skill with broad applications in various fields. The fundamental formula (Part / Whole) x 100% provides a reliable method for solving most percentage problems. By understanding the underlying principles and practicing regularly, you can confidently tackle percentage calculations and apply this skill to make informed decisions in your daily life and professional endeavors. Remember, the answer to "4 is what percent of 15?" is approximately 26.67%, but the real takeaway is the understanding of the process itself, which will allow you to solve countless other percentage problems.
Latest Posts
Latest Posts
-
70 G De Farine En Cuillere A Soupe
May 09, 2025
-
829 Rounded To The Nearest Ten
May 09, 2025
-
How Much Candy Do I Need For Halloween
May 09, 2025
-
How Many Cups Are In 48 Ounces
May 09, 2025
-
How Many Significant Figures Does 10 0 Have
May 09, 2025
Related Post
Thank you for visiting our website which covers about 4 Is What Percent Of 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.